CPLEXのモデルは様々な言語で書くことができます。
昔からあるOPLという言語とPythonのライブラリであるdocplexを使ったほぼ同じ内容のサンプルがあり、以下のそれぞれの記事で読み解きました。このサンプルをつかってOPLとdocplexとの違いを比較してみます。
最初に比較ポイントをまとめました。
| No | 項目 | OPL | docplex |
|---|---|---|---|
| 1 | 宣言型実行か逐次実行か | △宣言型なので基本的には、部分的実行や連続求解ができない。一応手続き型のOPLScriptはある。 | 〇順次実行が可能。部分実行や連続求解もできる。 |
| 2 | データ入力 | △datを用意しないといけない | 〇csvでもなんでもPythonのレベルで読める |
| 3 | データ加工 | △処理前、処理後に行うのが基本 | 〇処理前、処理後もシームレスに加工が行える |
| 3 | データ可視化 | △ガントチャートは簡単に出せるがそれ以上はできない。 | 〇コーディングは必要だが自由 |
| 4 | 決定変数の多次元データ構造 | 〇多次元配列。Keyに文字列のセットも使える | △list,dict,matrix,cubeなど、アクセスはやや面倒。 |
| 5 | 決定変数のスパースな行列構造 | △制約などをつくることで対応 | 〇dictを使うことでスパースな決定変数の行列をつくることができる |
| 6 | 決定変数の解の参照 | 〇問題ブラウザで簡単にみれる | △dictなどのなかからvalueを取り出して、solution_valueで参照しないといけない |
| 7 | 制約や決定変数の展開 | 〇定義した形で後から参照できる | △展開されてしまうので長いと見づらい |
| 8 | スラックの表示 | 〇問題ブラウザで簡単にみれる | △加工が必要 |
個人的な全体的感想としては、モデルと解の可読性という意味ではOPLの方が高いと思います。
一方で、docplexは様々なデータ加工や連続求解などができて便利だと思いました。可読性もプログラムを書くことで補うことができると思いました。
以下はそれぞれの項目について、比較をしていきます。
1.宣言型言語か手続き型言語か
OPL
OPLはモデルを記述する宣言型言語なので、全てのモデル記述を書き終えて実行するまで途中経過はわかりません。実行=求解なので、solveの命令はありません。
OPLにもOPL Scriptという手続き型言語が一応ありますが、これを使って、例えば2つのモデルの求解を行った場合はCPLEX Optimization Studioの機能の問題ビューアーなどは利用できません。
docplex
Python(docplex)は手続き型言語なので、solve()を実行するまでの宣言の状況を確認することもできます。
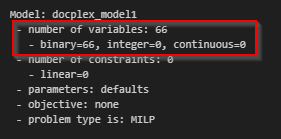
例えば、決定変数の定義途中の段階でもprint_information()で定義の状況を確認できます。
open_vars = warehouse_model.binary_var_dict(keys=warehouses, name='open')
supply_vars = warehouse_model.binary_var_matrix(keys1=warehouses, keys2=stores, name='supply')
warehouse_model.print_information()
また、同じ Python コードでモデルを変更しながら、複数回解いていくこともできます。
例えば例のなかでは、総コストの最適化をした後に開設コストを優先して最小化していました。設定変更後にwarehouse_model.solve()が再度行われています。
# 開設コストを優先して最小化する
warehouse_model.set_multi_objective(
sense="min", exprs=[total_opening_cost, total_supply_cost], priorities=[1, 0])
ok = warehouse_model.solve()
このように連続的に求解をしたり、別のモデルをつくって比較したりする場合は、もともと手続き型言語のPythonのほうが使いやすいと思います。
2.データの入力
OPL
OPLは.modファイルと別につくった.datファイルからデータを読み込む形式です。
{string} Warehouses = ...;
//各店舗と倉庫間の輸送費
int SupplyCost[Stores][Warehouses] = ...;
Warehouses = {Bonn,Bordeaux,London,Paris,Rome};
SupplyCost = [
[ 20, 24, 11, 25, 30 ],
[ 28, 27, 82, 83, 74 ],
[ 74, 97, 71, 96, 70 ],
[ 2, 55, 73, 69, 61 ],
[ 46, 96, 59, 83, 4 ],
[ 42, 22, 29, 67, 59 ],
[ 1, 5, 73, 59, 56 ],
[ 10, 73, 13, 43, 96 ],
[ 93, 35, 63, 85, 46 ],
[ 47, 65, 55, 71, 95 ] ];
このようにモデルとデータをわけることで、様々にデータを変えて求解することができます。
一方でこの形式は、様々なデータが一つのファイルに入る若干特殊な形式で、CSVなどをそのまま読むことはできません。
docplex
CSVでもJSONでもRDBでも、Pythonで読めるデータであればそのまま読み込んで利用することができます。
3.データの加工や可視化
OPL
さまざま関数は用意されていますが、例えば正規表現などをつかった加工はできませんので、処理前や処理後に行います。グラフもCPのスケジューリングのガントチャートは表示可能ですが、それ以上の処理は別の仕組みが必要です。
docplex
汎用言語のPythonでは、様々な加工や可視化が可能です。
例えば、例の中では決定変数の値をsolution_valueで取り出し、対応するsupply_costsの合計(sum)を計算してグラフ出力しています。
supply_cost_by_warehouse = [sum(supply_costs[w][s.id - 1]
for s in stores if supply_vars[w,s].solution_value >= 0.9)
for w in warehouses]
wh_labels = [w.id for w in warehouses]
display_costs(supply_cost_by_warehouse, wh_labels, None)
4.多次元データ構造
最適化では多次元データの操作をたくさん行います。その使いやすさの違いを考えます。
OPL
Pythonなど一般的な言語では配列の添え字は整数になります。しかし、整数だけだとデータの中身の理解が難しくなります。
OPL多次元配列の添え字にセット型も使えます。これはとても強力で可読性が高まります。
{string} Warehouses = {Bonn,Bordeaux,London,Paris,Rome};
range Stores = 0..9;
////決定変数
//倉庫の開設の有無
dvar boolean Open[Warehouses];
//倉庫と店舗の供給の有無
dvar boolean Supply[Stores][Warehouses];
配列なのですが、Bonnのようなセットの文字列を添え字にしたアクセスが可能です。
Supply[0]["Bonn"] <= Open["Bonn"]
docplex
docplexでは、binary_varのような単一の決定変数オブジェクトに加えて、以下のような決定変数のデータ構造を用意しています。
binary_var_list(keys, lb=None, ub=None, name=, key_format=None)
binary_var_dict(keys, lb=None, ub=None, name=None, key_format=None)
binary_var_matrix(keys1, keys2, name=None, key_format=None)
binary_var_cube(keys1, keys2, keys3, name=None, key_format=None)
list
listは配列なので、添え字が整数になります。以下のように[0]というアクセスになります。
openl_vars = warehouse_model.binary_var_list(keys=warehouses, name='openl')
print(openl_vars[0])
そして中身は決定変数オブジェクトになります。決定変数の名前はname+'_'+Keyの文字列表現です(この例だとopenl_Bonn)。決定変数自体は配列になっていません。配列の中身に決定変数オブジェクトが入っているという構造です。決定変数自体はリスト構造ではないということがOPLとの大きな違いです。
openl_Bonn
dict
dictは辞書型ということです。なので、添え字ではなくkeyでアクセスします。Keyはなんらかのオブジェクトになります。例では名前付きタプルのクラスを使っていました。ですので、以下のように[TWareHouse(id='Bonn', capacity=1, fixed_cost=20)]というアクセスになります。
open_vars = warehouse_model.binary_var_dict(keys=warehouses, name='open')
print(open_vars[TWareHouse(id='Bonn', capacity=1, fixed_cost=20)])
そして中身はやはり決定変数オブジェクトになります。決定変数の名前はname+'_'+Keyの文字列表現です(この例だとopen_Bonn)。
open_Bonn
クラスがkeyだと複雑に見えますが。もちろんKeyは文字列でも可能です。以下は['Bonn','Bordeaux','Brussels']の文字列リストをkeysにしています。
openls_vars = warehouse_model.binary_var_dict(
keys=['Bonn','Bordeaux','Brussels'], name='openls')
print(openls_vars))
print(openls_vars['Bonn'])
{'Bonn': docplex.mp.Var(type=B,name='openls_Bonn'), 'Bordeaux': docplex.mp.Var(type=B,name='openls_Bordeaux'), 'Brussels': docplex.mp.Var(type=B,name='openls_Brussels')}
openls_Bonn
matrix
matrixは二次元のデータ構造です。dictと異なりkey1とkey2という二つのkeyでアクセスします。例ではkeys1=warehousesとkeys2=storesの二つのKeyで定義されています。
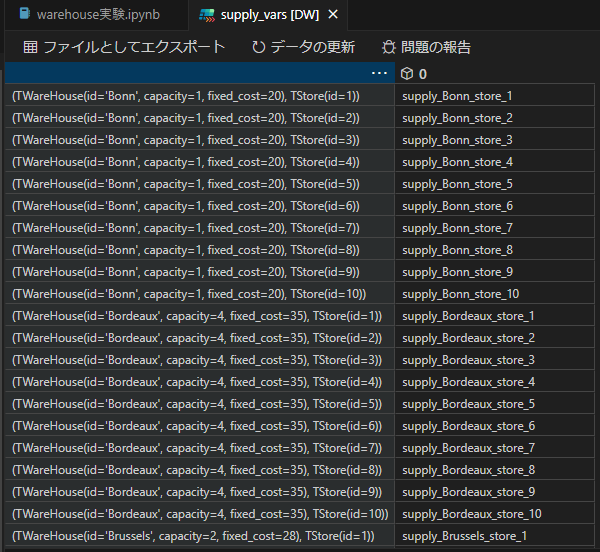
例ではTWareHouseとTStoreの名前付きタプルのクラスを使っていました。ですので、以下のように[(TWareHouse(id='Bonn', capacity=1, fixed_cost=20),TStore(id=1))]というアクセスになります。
supply_vars = warehouse_model.binary_var_matrix(keys1=warehouses, keys2=stores, name='supply')
print(supply_vars[(TWareHouse(id='Bonn', capacity=1, fixed_cost=20),TStore(id=1))])
そして中身はやはり決定変数オブジェクトになります。決定変数の名前はname+''+Key1+''+Key2の文字列表現です(この例だとsupply_Bonn_store_1)。
supply_Bonn_store_1
ただ、実はmatrixと言いながら、実体はdictと同じ辞書型です。ですので、Keyの部分をタプルにしてあげるとbinary_var_dictでも同じものができます。すっきり書けるというメリットのためにbinary_var_matrixがあります。
supplyd_vars = warehouse_model.binary_var_dict(
keys=[(w,s) for w in warehouses for s in stores], name='supplyd')
print(supply_vars)
print(supplyd_vars)
cubeもkeyが3つあるだけで、実体はdictです。
実体が配列ではないので微妙にKeyアクセスがしづらいかなと個人的には思います。
5.スパースな配列の表現
例えば、BonnからStore3とStore5への輸送路は業務上不可能な場合に、配列だと倉庫×店舗で全てのセルに決定変数ができてしまいます。そのような配列の表現について考えます。
OPL
配列で定義してしまうとすべてのセルに決定変数ができてしまうので、次のような設定させないための制約が必要です(店舗のIDが0始まりなので、添え字がずれていて、Store3が[2]になっています)。
subject to{
ctExcludeSupplyBonn_2:
Supply[2]["Bonn"] <= 0;
ctExcludeSupplyBonn_4:
Supply[4]["Bonn"] <= 0;
}
docplex
binary_var_dictなら辞書型であるため、スパースな配列を表現することができるというメリットがあります。
OPLの例でみたように、配列だとn×mで全てのカラムに決定変数ができてしまいますので、制約で省く必要があります。
しかし、辞書型だとそもそも決定変数を定義しないことができます。これはスパースの度合いが高いデータの場合は、メモリや計算量の面からみても有利です。
以下のようなコードで除外部分のある辞書を作る事ができます。BonnからStore3とStore5への決定変数を除外しています。
excludelist=[(TWareHouse(id='Bonn', capacity=1, fixed_cost=20),TStore(id=3)),
(TWareHouse(id='Bonn', capacity=1, fixed_cost=20),TStore(id=5))]
supplyd2_vars = warehouse_model.binary_var_dict(
keys=[(w,s) for w in warehouses for s in stores if (w,s) not in excludelist ], name='supplyd2')
BonnからStore3とStore5は定義がありません。一方でBordeauxからはStore3とStore5は定義があります。

6.解の参照
Solve後の解の参照について比較します。
OPL
問題ブラウザのデータビューで簡単に結果を見ることができます。これはとても便利です。
以下の2次元の決定変数の結果をクリックするだけで表示できます。
//倉庫と店舗の供給の有無
dvar boolean Supply[Stores][Warehouses];
docplex
binary_var_matrixなどに入っているのはsupply_Bonn_store_1などの決定変数オブジェクトなので、そのまま結果は表示できません。
解の中身を見るためにはsolution_valueで取り出す必要があります。また、先にも述べたようにbinary_var_matrixなどは実際には辞書型なので、表形式で表示させようとすると、プログラムでData Frameなどに加工する必要があります。
以下のプログラムではdictのkeyから倉庫と店舗のIDを抜き出し、dictのvalueからsolution_valueを求めてData Frameにして、さらにPivotをかけています。
supply_vars_w = [k[0].id for k in supply_vars.keys()]
supply_vars_s = [k[1].id for k in supply_vars.keys()]
supply_vars_v = [round(v.solution_value) for v in supply_vars.values()]
df_suuply = pd.DataFrame({"warehouse": supply_vars_w,
"store": supply_vars_s,
"supply": supply_vars_v})
df_suuply.pivot_table(values="supply", index="store",
columns="warehouse")
7.制約や決定変数の展開
OPL
複数の制約に一つの名前をつけて(この例ではctEachStoreHasOneWarehouse)、問題ブラウザのデータビューで定義した制約や決定変数を見ることができます。この際、sumなどの集合演算定義をそのまま参照できます。
制約をクリックするだけで表示できます。
forall( s in Stores )
ctEachStoreHasOneWarehouse:
sum( w in Warehouses ) Supply[s][w] == 1;
またsum関数がそのまま残っていますので、コンパクトで読みやすいです。

docplex
ctname=f'ct01_{str(s)}'のようにネーミングルールをつけて制約をつくっておけば、get_constraint_by_nameで、関連制約する定義の一覧を作る事ができます。
for s in stores:
warehouse_model.add_constraint(
warehouse_model.sum(supply_vars[w, s] for w in warehouses) == 1,
ctname=f'ct01_{str(s)}')
for s in stores:
print(warehouse_model.get_constraint_by_name(f'ct01_{str(s)}'))
参照された定義ではsum関数がなくなって、supply_Bonn_store_1+supply_Bordeaux_store_1+supply_Brussels_store_1+supply_London_store_1+supply_Paris_store_1+supply_Rome_store_1というように、個々の決定変数の和に展開されています。
これは長くなると可読性が下がります。
ct01_store_1: supply_Bonn_store_1+supply_Bordeaux_store_1+supply_Brussels_store_1+supply_London_store_1+supply_Paris_store_1+supply_Rome_store_1 == 1
ct01_store_2: supply_Bonn_store_2+supply_Bordeaux_store_2+supply_Brussels_store_2+supply_London_store_2+supply_Paris_store_2+supply_Rome_store_2 == 1
ct01_store_3: supply_Bonn_store_3+supply_Bordeaux_store_3+supply_Brussels_store_3+supply_London_store_3+supply_Paris_store_3+supply_Rome_store_3 == 1
ct01_store_4: supply_Bonn_store_4+supply_Bordeaux_store_4+supply_Brussels_store_4+supply_London_store_4+supply_Paris_store_4+supply_Rome_store_4 == 1
ct01_store_5: supply_Bonn_store_5+supply_Bordeaux_store_5+supply_Brussels_store_5+supply_London_store_5+supply_Paris_store_5+supply_Rome_store_5 == 1
ct01_store_6: supply_Bonn_store_6+supply_Bordeaux_store_6+supply_Brussels_store_6+supply_London_store_6+supply_Paris_store_6+supply_Rome_store_6 == 1
ct01_store_7: supply_Bonn_store_7+supply_Bordeaux_store_7+supply_Brussels_store_7+supply_London_store_7+supply_Paris_store_7+supply_Rome_store_7 == 1
ct01_store_8: supply_Bonn_store_8+supply_Bordeaux_store_8+supply_Brussels_store_8+supply_London_store_8+supply_Paris_store_8+supply_Rome_store_8 == 1
ct01_store_9: supply_Bonn_store_9+supply_Bordeaux_store_9+supply_Brussels_store_9+supply_London_store_9+supply_Paris_store_9+supply_Rome_store_9 == 1
ct01_store_10: supply_Bonn_store_10+supply_Bordeaux_store_10+supply_Brussels_store_10+supply_London_store_10+supply_Paris_store_10+supply_Rome_store_10 == 1
8.スラックの表示
OPL
問題ブラウザのデータビューで定義した制約のスラックを一覧で確認できます。
制約をクリックするだけで表示できます。
forall( w in Warehouses )
ctMaxUseOfWarehouse:
sum( s in Stores ) Supply[s][w] <= Capacity[w];
docplex
モデルから、get_constraint_by_nameで制約オブジェクトをみつけて、slack_valuesで取得します。
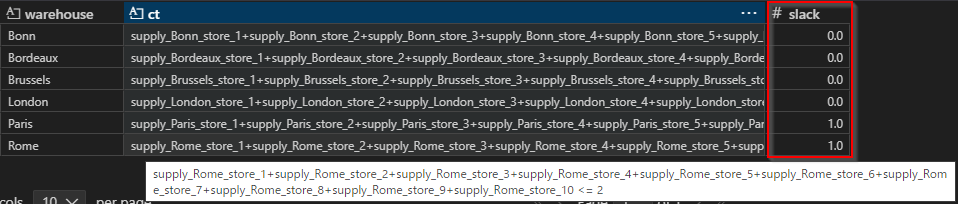
制約の定義と並べて表形式で確認しようとすると、プログラムでData Frameなどに加工する必要があります。制約の定義をコンパクトにするために_extract_after_colonという:を取り出すようなローカル変数も作っています。
def _extract_after_colon(s): return s[s.find(':') + 1:] if ':' in s else ''
warehouse = [w.id for w in warehouses]
ct3n = [_extract_after_colon(
warehouse_model.get_constraint_by_name(f'ct03_{str(w)}').to_string())
for w in warehouses]
ct3s = [warehouse_model.get_constraint_by_name(f'ct03_{str(w)}').slack_value
for w in warehouses]
pd.DataFrame({"warehouse": warehouse,
'ct': ct3n,
'slack': ct3s})
参考
OPL vs Python docplex. Choosing between a dedicated language… | by AlainChabrier | Medium
(5) Optimization (aka prescriptive analytics) : Should we write the model in a modeling language or a general programming language ? | LinkedIn