参考文献: ゼロから作るDeep Learning―Pythonで学ぶディープラーニングの理論と実装
まだ未熟なため、不適切な部分が散見されると思いますが、温かい目で見てください。
導入
大学の講義において、誤差逆伝搬法の勾配計算は、難解な数式で計算すると思います。ですが、pytorchなどのプログラム上での実装ではそういった数式ではなく計算グラフを用いて勾配計算することが多いです。
そのため、大学の講義の流れでpytorchに触れると、requires_gradというなぞの引数によって大混乱状態になると思います。
pytorch.Tensorの引数であるrequires_gradは、計算グラフのノードとして、このtensorを追加しますか？っていう意味です。
どういう意味でしょうか？
そこで今回は、計算グラフをざっくりと解説します。
計算グラフとは
計算グラフとは、複雑な計算を単純な計算に分解し、グラフで表現したものです。
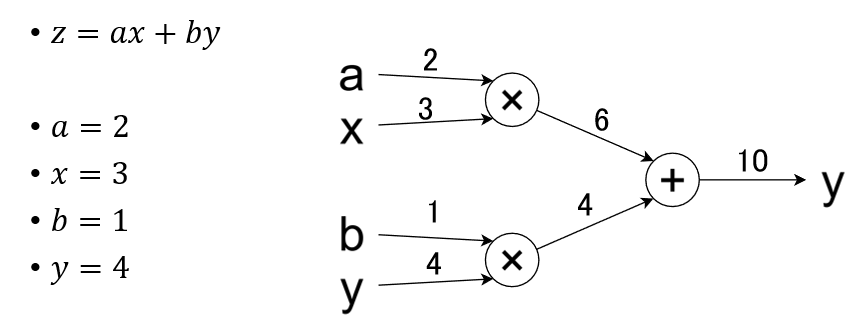
x円のりんごをa個、y円のバナナをb個買うときを考えます。
合計金額は $y=ax+by$で表せます。これを計算グラフで表すと以下のようになります。
この図でいう左から右への計算を、ニューラルネットワークの文脈で順伝搬といいます。
(+)みたいなやつは入力の和を返すもので、加算ノードと呼びます。
(×)みたいなやつは入力の積を返すもので、乗算ノードと呼びます。
では、勾配の計算をしてみましょう。
勾配計算は右から左への計算で、ニューラルネットワークの文脈では逆伝搬と言います。
今回は、yに対するaの勾配を計算します。
$s=ax$, $t=by$とします。連鎖率を用いると、以下の等式が成り立ちます。
$\frac{\partial y}{\partial a}
=\frac{\partial y}{\partial y}\cdot
\frac{\partial y}{\partial s}\cdot
\frac{\partial s}{\partial a}$
計算グラフでは、以下のように考えます。
このように考えると、入力を受け取って出力を返す関数の連なりとして勾配を計算できています。
各ノードの入出力を以下の表にまとめました。
| ノード | 入力 | 出力 |
|---|---|---|
| 終点 | - | $\frac{\partial y}{\partial y}(=1)$ |
| 加算ノード | $\frac{\partial y}{\partial y}(=1)$ | $\frac{\partial y}{\partial y}\cdot\frac{\partial y}{\partial s}(=\frac{\partial y}{\partial s})$ |
| 乗算ノード | $\frac{\partial y}{\partial y}\cdot\frac{\partial y}{\partial s}(=\frac{\partial y}{\partial s})$ | $\frac{\partial y}{\partial y}\cdot\frac{\partial y}{\partial s}\cdot\frac{\partial s}{\partial a}(=\frac{\partial y}{\partial a})$ |
| 始点 | $\frac{\partial y}{\partial y}\cdot\frac{\partial y}{\partial s}\cdot\frac{\partial s}{\partial a}(=\frac{\partial y}{\partial a})$ | - |
最終的に、aの勾配を求めることができています。
よく見ると、逆伝搬のとき各ノードは、順伝搬のときの出力に対する逆伝搬のときの入力の勾配を乗算しています。
その結果として、逆伝搬のときの各ノードの出力は、yに対する順伝搬のときの各ノードの入力の勾配になっています。
計算グラフの威力
ここまでは、計算グラフの計算の流れを見ていきました。
ここからは、具体例を交えて計算グラフの威力を見ていきましょう。
まず、先ほどの例で微分の値を実際に計算してみます。
↑この図の微分を計算すると
このようになりました。
一例だけでは分かりにくいかもしれませんが、実は、逆伝搬において、加算ノードは入力をそのまま出力し、乗算ノードは進む先のノード以外から順伝搬された値の積を出力します。
仕組みは、以下の関数について偏微分してみると分かります。
add(x,y)=x+y
mul(x,y)=xy
すると、勾配計算をプログラム上で実装したい場合は、基本的な演算について順伝搬のときの入出力、逆伝搬のときの入出力を定義すればできそうです。
pytorchでいうところの、net()とnet.backward()ですね。
ここで、代数的な勾配計算と、計算グラフによる勾配計算をプログラム上で実装することを考えてみましょう。
代数的な実装では、各計算をもとに計算式を求めます。その計算式の勾配を求めるために複雑な微分計算をする必要があります。計算終了後、実際の値を代入して勾配を求めます。
計算グラフを用いた実装では、各計算をもとに計算グラフを作成します。計算グラフ上のノードに値を渡していき勾配を直接求めます。
比較すると、計算グラフがなぜpytorchの実装で用いられているかが分かると思います。
pytorch.Tensorの引数であるrequires_gradは、この計算グラフのノードとして、このtensorを追加しますか？っていう意味です。
この記事を通して、なるほどとなれば幸いです。
例題
実際に変数bの勾配を求めて計算グラフを理解しましょう。
以下のようになります。
まず1があって、加算ノードではそのまま流すので1、乗算ノードでは進む先以外(y)からきた4を掛けるので1x4となり、最終的に、bの勾配は4と分かります。
発展課題
以下のような関数はReLU関数と呼ばれます。
f(x) = \left\{
\begin{array}{ll}
x & (x \ge 0) \\
0 & (x \lt 0)
\end{array}
\right.
この関数について、微分計算してみましょう。
答えは、以下のようになります。
f'(x) = \left\{
\begin{array}{ll}
1 & (x \ge 0)\\
0 & (x \lt 0)
\end{array}
\right.
ReLU関数の逆伝搬を考えてみましょう。
逆伝搬は、入力が正のときのみ通す動きをします。
例題の加算ノードをReLU関数に置き換えて、微分計算と計算ノードの2つの方法で勾配計算をしてみましょう。
ニューラルネットワークでは、このような分岐を含む関数をよく用います。
複雑な計算式の中に、分岐がたくさんある状況を考えてみてください...