カメラキャリブレーションはレンズの歪み補正などに使われますが、それぞれの係数がどう影響を及ぼしているのかわかりにくく感じます。
そこで直感的に理解できるようにしてみようと思います。
カメラキャリブレーションとは
理想的なピンホールカメラモデルでない限り、左図のように画像は歪んでいます。
カメラ固有の歪み係数を求めることで、このように歪んだ画像を補正することができます。
カメラキャリブレーションの仕組み
カメラキャリブレーションを行う際は、チェッカーボードと呼ばれるものを印刷します。
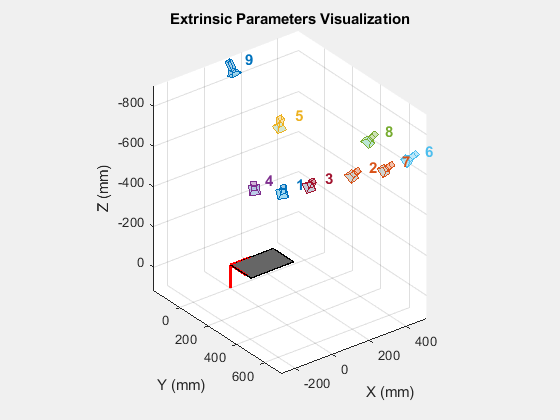
パラメータを計測したいカメラでその写真をあらゆる角度から何十枚も撮影します。
これでカメラの二次元座標 $x$ と空間の三次元座標 $X$ との対応が取れるようになります。
x = P X
この $P$ がカメラマトリックスです。3行4列で、連立方程式で求まります。
P = K [R|t]
$P$ は上三角行列 $K$ と正規直行行列 $R$ に分解することができて、
$K$ ...... 内部パラメータ、Intrinsic Parameter (焦点距離、光学中心、せん断係数)
$[R|t]$ ... 外部パラメータ、Extrinsic Parameter (カメラの回転と変換)
となります。
内部パラメータ
この内部パラメータ $K$ は
K = \begin{pmatrix}
f_x & s & c_x \\
0 & f_y & c_y \\
0 & 0 & 1 \\
\end{pmatrix}
となっていて、焦点距離 $(f_x, f_y)$, 光学中心 $(c_x, c_y)$, せん断係数 $s$ を表します。
実装
PythonではOpenCVを使って以下のように $K$ (mtx)が求まります。
# チェッカーボードから点を検出
ret, corners = cv2.findChessboardCorners(gray, (8,6), None)
# キャリブレーション
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, img_size,None,None)
# 歪み補正
dst = cv2.undistort(img, mtx, dist, None, newMtx)
直感的理解
それぞれ焦点距離、光学中心、せん断係数などのパラメータをアニメーションしてみましょう。
求めたカメラマトリックスから、対象のパラメータのみを変化させています。
元画像
焦点距離
無限遠→適正焦点距離→小さい
(1) $f_x, f_y$
(2) $f_x$
(3) $f_y$
光学中心
負→適正位置→正
(1) $c_x$
(1) $c_y$
せん断係数
負→適正値→正
英語ではSkewです。
まとめ
いかがだったでしょうか。
カメラキャリブレーションは歪みの補正に使われるということがわかりました。
フューチャーワーク
半径方向の歪み係数、円周方向の歪み係数についてもやりたいです。
画像引用
https://github.com/DavidWangWood/Camera-Calibration-Python
https://jp.mathworks.com/help/vision/examples/evaluating-the-accuracy-of-single-camera-calibration.html