【unity】Mesh (genus_n) Cutting 機能の試験実装

概要

種数 (幾何学的な閉曲面の数) が 0 以上 のオブジェクトや、非凸多角形オブジェクトを、特定の平面で分割する機能がなかったため、これを実現する機能の試験実装を行った。そして、機能のブラッシュアップ・修正のための、アルゴリズムとその実装方法について共有するものである。

自分の言葉で表せば、ドーナツとかナルトとか伊達巻を斬ったときに、おいしそうな断面を作れる機能が欲しかったので、自分なりの試験実装をしました。しかし、まずいところ怪しいところが多いはずなので、他人の力を借りようということです！

早速ではありますが、切断の実行結果は 図1 の通りです ↓↓↓
この機能のサンプルシーンを github に公開しているので、試したい方はぜひ！
また、この機能の試験実装に際して、参考にしたものは参考文献に記載しています。Mesh の操作やアルゴリズムについて詳載されていますので、ぜひ合わせてご確認ください。

切断実行結果

Cube	Torus	Cube has Hole
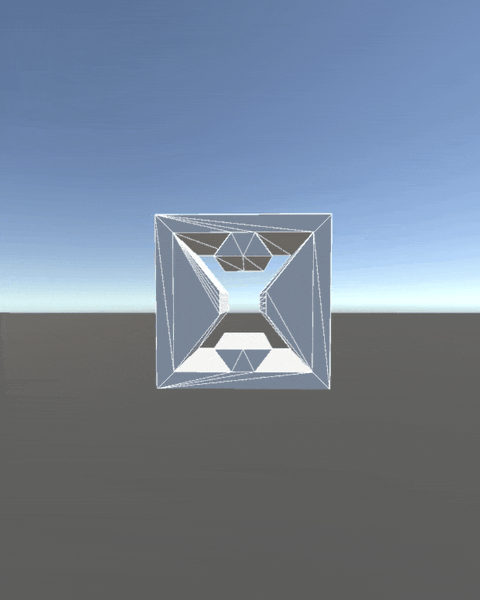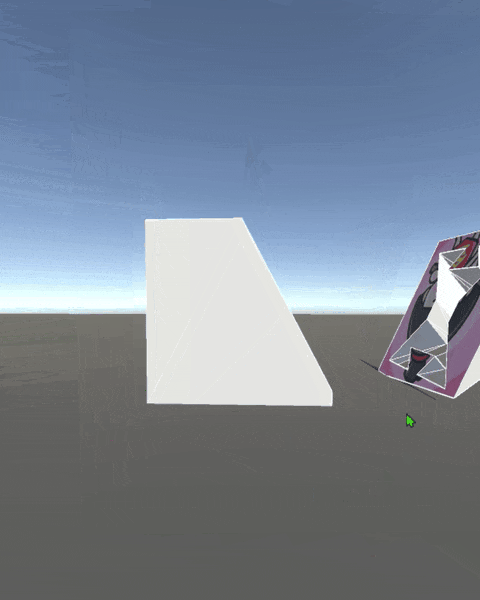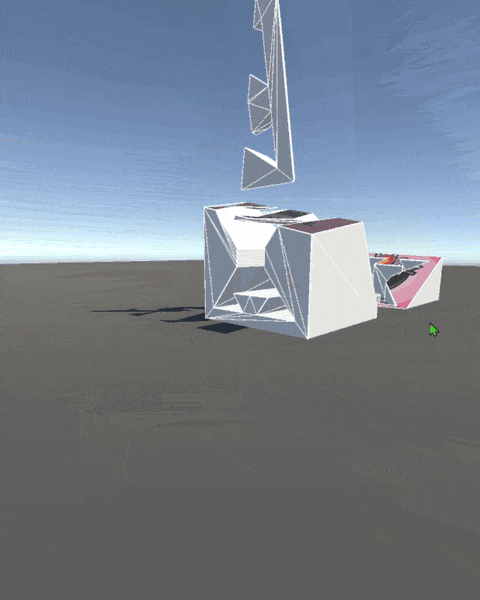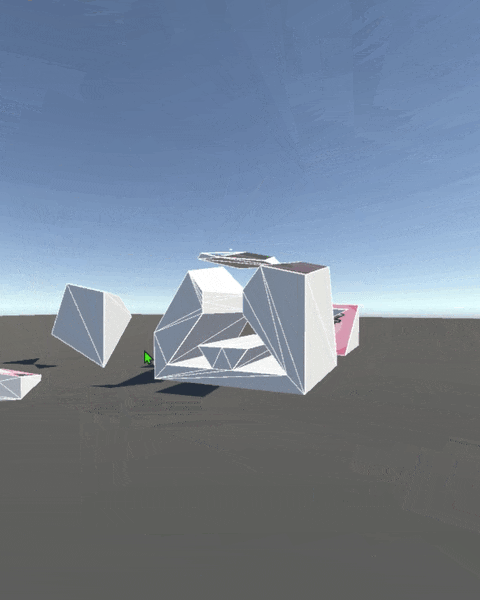単純な多面体	穿孔多面体	非凸な孔を持つ穿孔多面体

図1: 切断実行結果

目次

1. 概要
   • 切断実行結果
2. 切断機能の実装
   • クラス図
   • 概略フロー
   • 重要度高めクラスの簡単な役割・処理説明
     • BaseSurfacePolygonBuffer
     • LinkedPolygonList
     • LinkedPolygon
     • CutSurfacePolygonBuffer
     • LinkedVertexList
     • LinkedVertex
     • DiagonalEdgeGenerator
     • MonotoneGeometryPathList
     • MonotoneGeometryPath
3. 参考文献
4. リポジトリへのリンク

切断機能の実装

この章での図や文章では、正確ではない説明や省いているものが大いに存在するので、細かい仕様はスクリプトを直接ご確認いただきたいです。

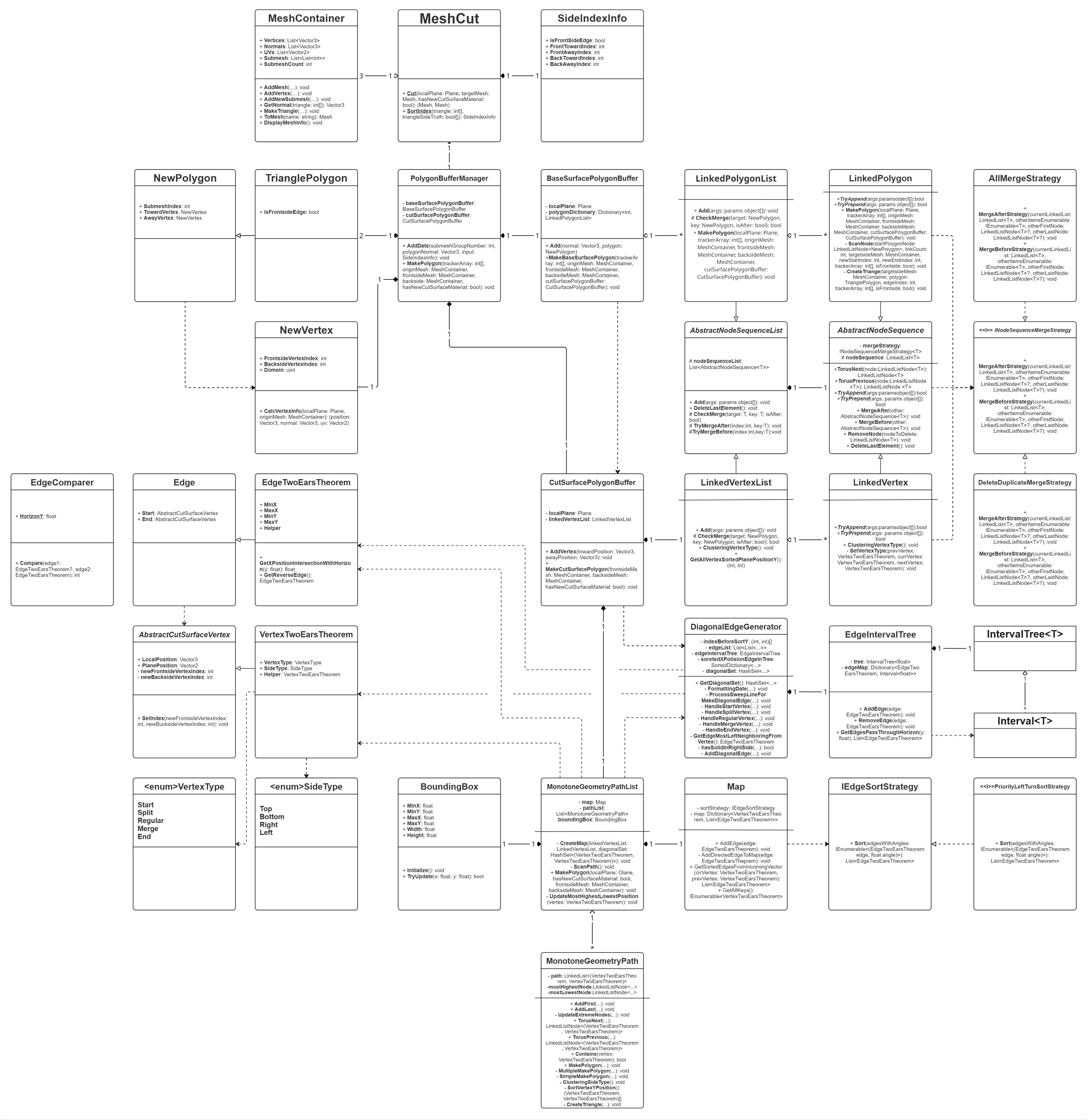
クラス図

図2: なんちゃってクラス図

概略フロー

• GameManager (図2 には未記載)
  1. 切断平面 (カッター) を用意する。
  2. カッターと切断対象のメッシュを MeshCut へ渡して切断処理を開始する。
• MeshCut
  1. メッシュのうち、三角形のポリゴンを構成する三頂点の間にカッターによる切断辺ができるか調べる。
  2. 切断辺ができるポリゴンの頂点の順番を整形して、バッファーに追加する。
     • PolygonBufferManager
       この追加はすべて base surface のバッファーに対して行う。
       • BaseSurfacePolygonBuffer
         base surface (切断前のサーフェス) 面
         1. 新しく追加されるポリゴンは、同じ法線をもつグループに配属される。
         2. さらに配属先では、既にあるものとのマージ判定を行ってから追加する。
       • CutSurfacePolygonBuffer - cut surface (切断後に新しくできるサーフェス) 面
         1. 切断平面上の図形を、単調な図形に分割する対角線を生成する。
         2. 対角線を加えてできる単調な図形ごとにグループ管理する。
  3. バッファーに格納されたポリゴン情報でポリゴンを再構築する。
     ここではまず base surface のポリゴンを再構築する。それによって生まれる副次的な情報で初めて、CutSurfacePolygonBuffer にポリゴン情報が蓄積され、これを基に cut surface のポリゴンを再構築する。

重要度高めクラスの簡単な役割・処理説明

BaseSurfacePolygonBuffer

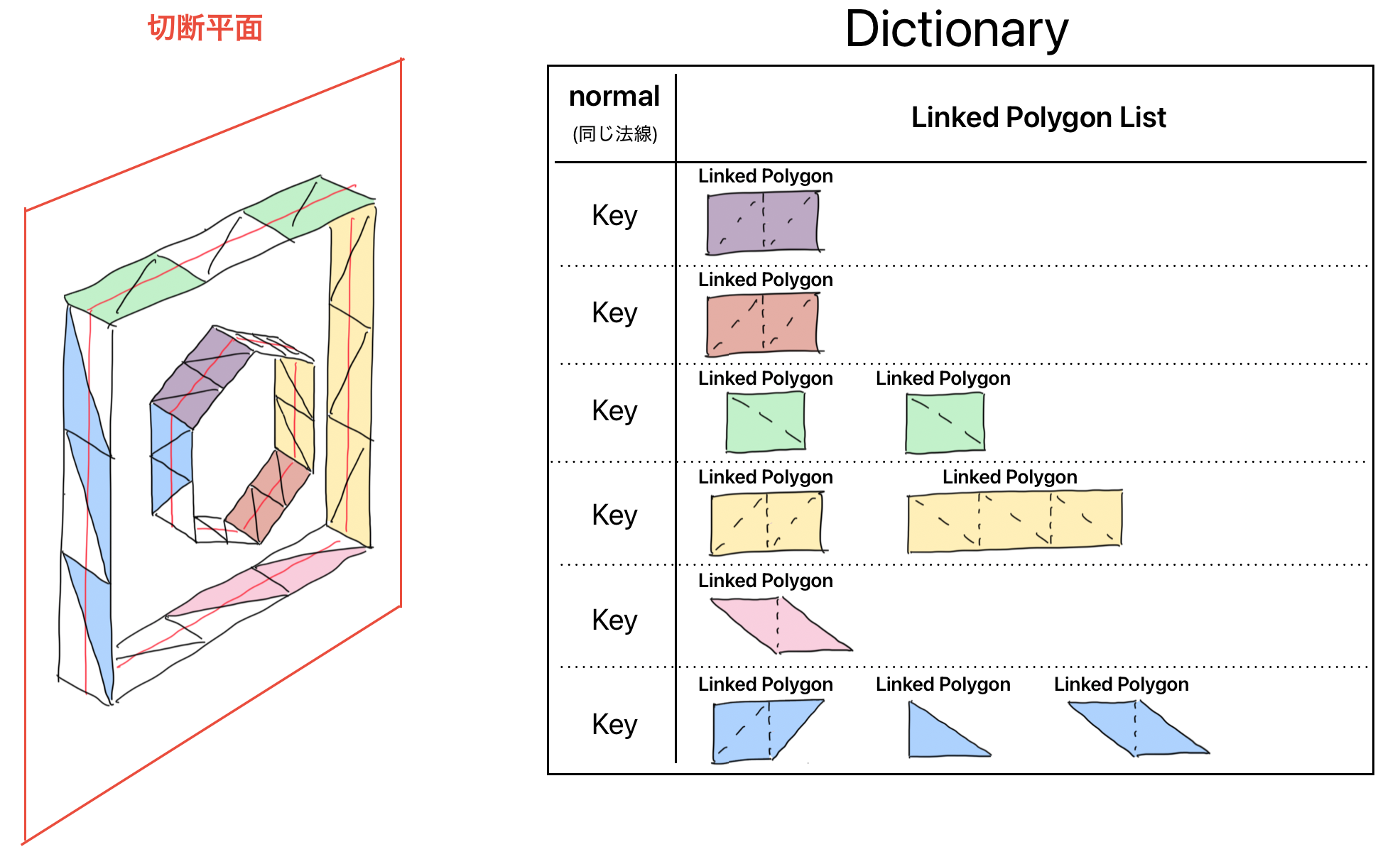
このクラスでは、切断対象のポリゴンを同じ法線のグループごとにまとめます。追加する際にポリゴンの法線を確認し、法線を key, LinkedPolygonList を value として辞書で管理しています。
切断平面を跨いだポリゴンにが格納されたバッファーイメージは 図3 のようになります。

図3: base surface バッファーの構成

LinkedPolygonList

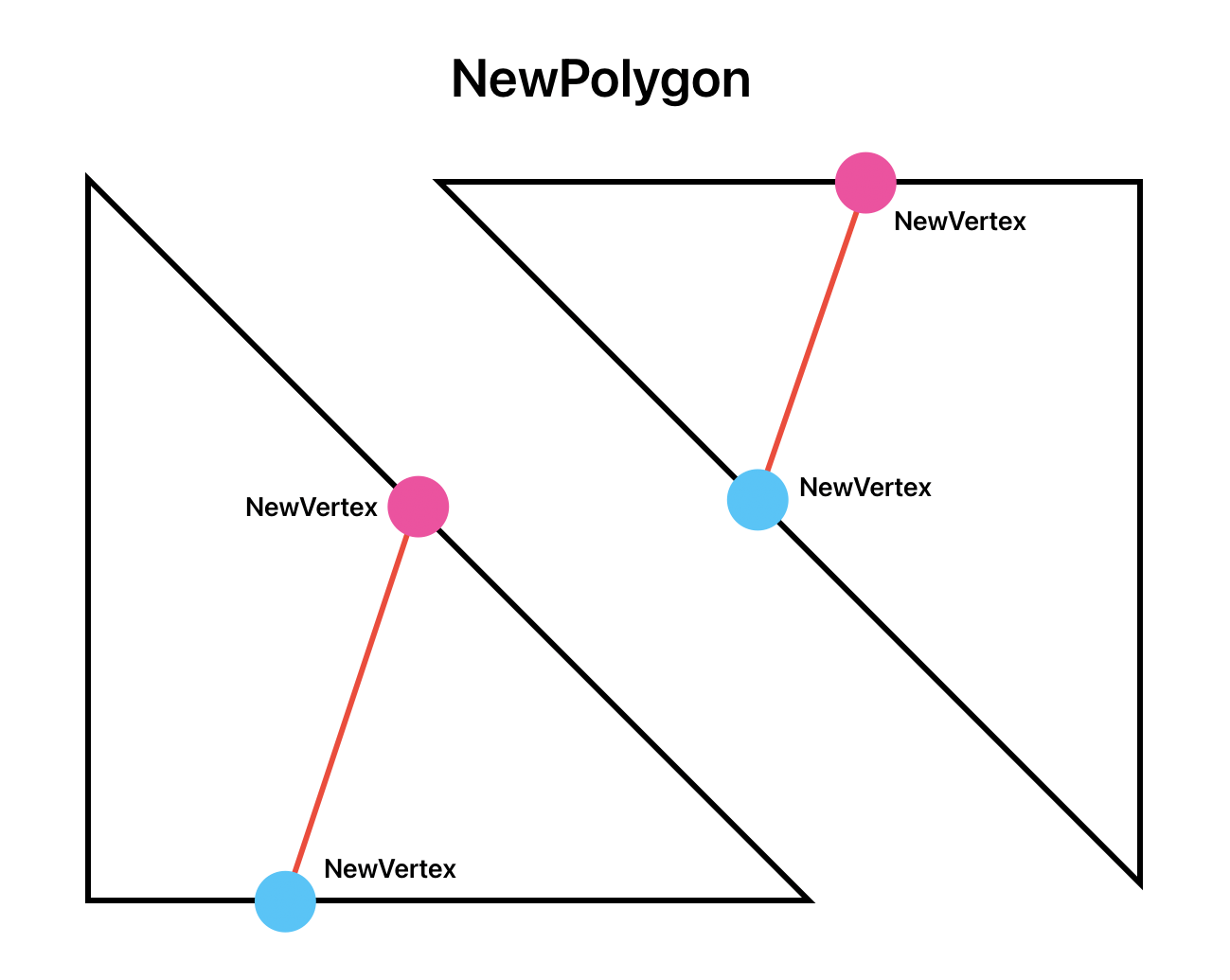
このクラスでは、マージ可能性のある要素 LinkedPolygon をリストで管理し、要素がリストに追加される毎に、現在管理しているすべての要素とのマージ判定を行います。マージのできるものはマージし、新しい 1 つの要素に改めて扱います。マージ判定は 図4 のうち、NewVertex が一致するかどうかで行います。このクラスへの追加操作の時間計算量は O(n) です。マージが発生する場合 O(n + m): (m は LinkedPolygon の数) です。

LinkedPolygon

このクラスは連結したポリゴンの塊です。内部的にはポリゴンを双方向リストで管理しています。このクラスへの追加操作の時間計算量は O(1) です。
また、「お前の持っているポリゴンの塊で新しいポリゴンを作れ！」と指示されたときに、頂点の増加を防ぎつつ、unity.Mesh による頂点の管理方法と同様の形式のポリゴンを生成します。そして、副産物として切断平面上の頂点群を CutSurfacePolygonBuffer へ追加します。

図4: NewPolygon クラス

CutSurfacePolygonBuffer

このクラスでは、切断平面上の図形を図形グループごとにまとめます。(対応付けのつもりで Polygon という名前をとっています。) このクラスへは、LinkedPolygon.MakePolygon() を通して頂点の追加が行われます。このクラスの内部で、LinkedVertexList によって頂点の管理をしています。
また、「お前の持っている切断平面上の図形の情報で新しいポリゴンを作れ！」と指示されときに、軸単調な図形へ分割するための対角線の生成呼び出しや、MonotoneGeometryPathList の生成をします。
このクラスで行われる切断平面上図形の処理遷移イメージは 図5 のようになります。

図5: cut surface 図形の状態遷移

LinkedVertexList

このクラスでは、マージ可能性のある要素 LinkedVertex をリストで管理し、要素がリストに追加される毎に、現在管理しているすべての要素とのマージ判定を行います。マージのできるものはマージし、新しい 1 つの要素に改めて扱います。このクラスへの追加操作の時間計算量は O(n) です。マージが発生する場合 O(n + m): (m は LinkedPolygon の数) です。ただし、LinkedPolygon.MakePolygon() による追加において、例外を除いてマージ処理は発生しません。

LinkedVertex

このクラスは連結した頂点の塊です。内部的にはポリゴンを双方向リストで管理しています。このクラスへの追加操作の時間計算量は O(1) です。

DiagonalEdgeGenerator

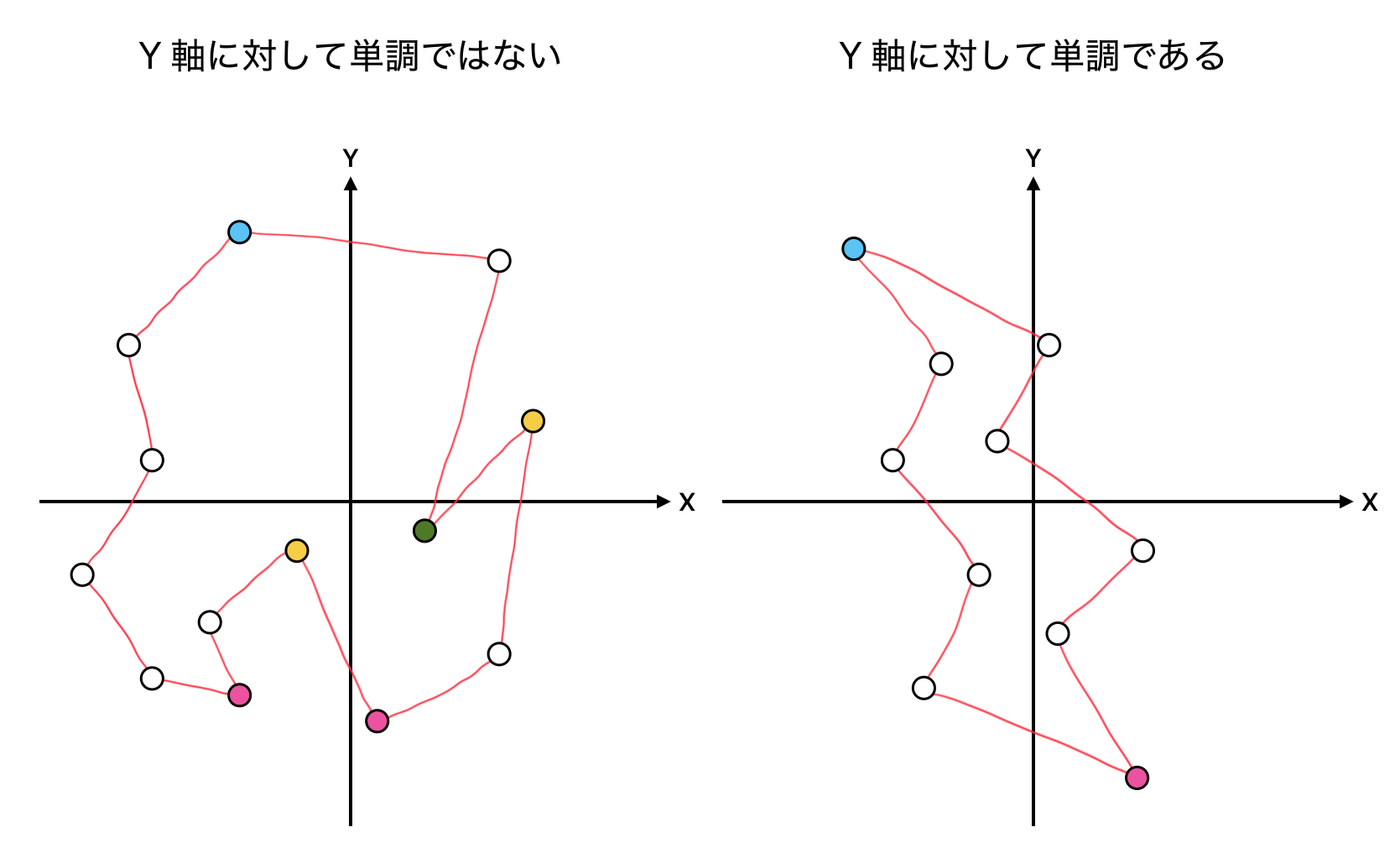
このクラスでは、切断平面上にできた図形を、軸単調な多角形に分割する対角線を生成します。ここでいう軸単調とは以下のような状態をいいます (図6)。

1. 切断平面に xy の直交座標系を導入する。
2. x または y のどちらかに着目して、図形の最大地点 (MAX) と最小地点 (min) をマークする。
3. このとき、MAX から min までを両側の境界で指でなぞったときに、着目した軸に対して単調減少 (常に減少) する。

この機能を実現するためには、対角線をグラフ探索をして生成するわけですが、図形の探索手法については　Plane Sweep Algorithm [5] を参考にしました。ただしこの手法では走査線と走査対象辺が水平の場合に処理に躓きます。また、走査対象の辺だけでなく、生成された対角線も走査線と水平の場合にはもっと致命的な問題が発生します。そこで、このクラスでは走査順の適切な順位付けと、水平な対角線の問題に対応できるようにしています。具体的な実装についてはスクリプトやコメントを直接見ていただいた方がわかると思います。
この走査の時間計算量はだいたい O(nlogn)です。

図6: Y 軸に対して...

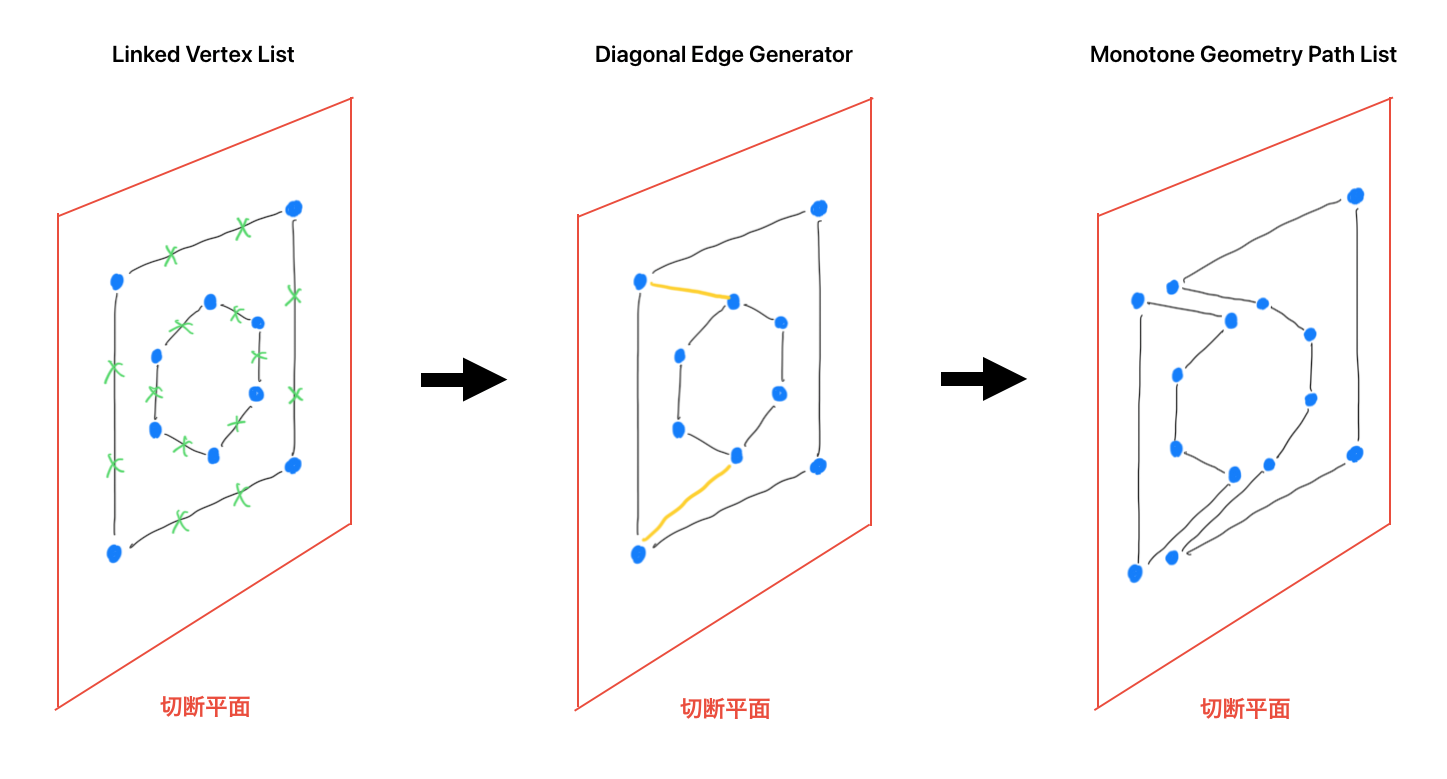
MonotoneGeometryPathList

このクラスでは、生成された対角線と元の図形の連結辺をもとに、軸単調な図形の連結辺リストを生成します。元の図形の連結辺たちは有向辺なので、新しく対角線を追加すると、その順序性が失われます。そこで、連結辺の再構築のための対角線の挿入では、双方向の辺を挿入することで順序性を保っています。(図7)
このクラスによる軸単調な図形の走査では、時間計算量が O(n^2) かかるので、改善点です。

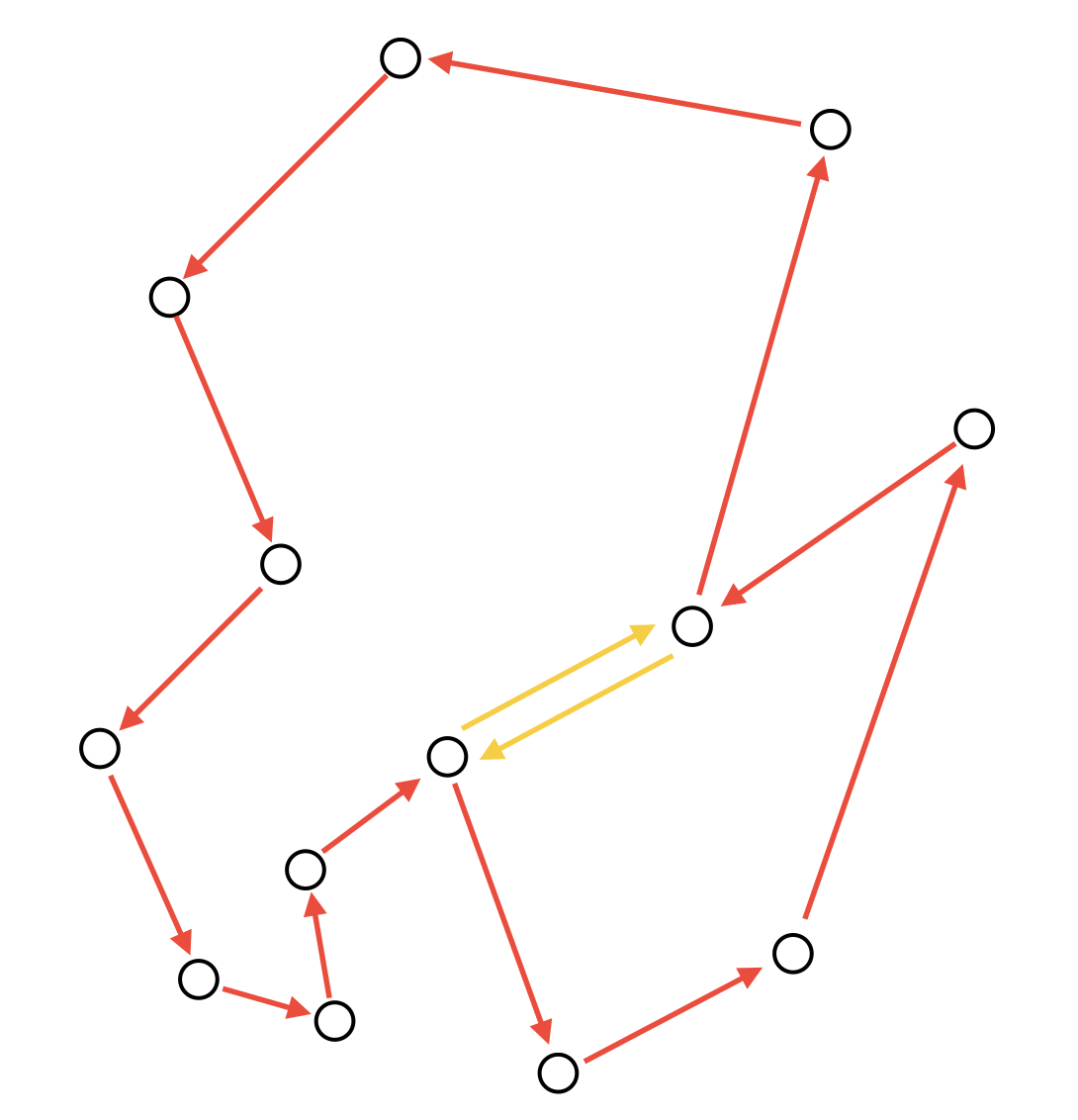
図7: 対角線の挿入

MonotoneGeometryPath

このクラスは、対角線によって軸単調に分割された図形ひとつの連結辺を持っています。(閉じたパスをただひとつ持っている。)
また、「お前の持っている切断平面上の図形の情報で新しいポリゴンを作れ！」と指示されときに、Two Ears Theorem によって三角形分割を行い、ポリゴンを生成します。
この操作の時間計算量はだいたい O(nlogn) です。

参考文献

[1] [Unity] メッシュカット (Mesh Cut) の高速化・高性能化をがんばる
[2] [Unity] Mesh Cut のサンプルを読む (メッシュの切断)
[3] assyの穴あき非凸多角形の三角形分割
[4] hugoscurti/mesh-cutter: Simple mesh cutting algorithm that ...
[5] de Berg, M., Cheong, O., van Kreveld, M., & Overmars, M. (2022). Computational geometry: Algorithms and applications (3rd ed., Japanese translation by T. Asano). Kindai Kagaku Sha. / ドバーグ, M., チョン, O., ファンクリベルド, M., & オーバマーズ, M.（著）, 浅野哲夫（訳）. (2022). コンピュータ・ジオメトリ ― 計算幾何学：アルゴリズムと応用（第3版）. 近代科学社.

リポジトリへのリンク