\newcommand{\OneTwo}[2]{\left(\begin{array}{cc} #1 & #2 \end{array} \right)}
\newcommand{\TwoOne}[2]{\left(\begin{array}{c} #1 \\ #2 \end{array} \right)}
\newcommand{\TwoTwo}[4]{\left(\begin{array}{cc} #1 & #2 \\ #3 & #4 \end{array} \right)}
\newcommand{\ThreeOne}[3]{\left(\begin{array}{c} #1 \\ #2 \\ #3 \end{array} \right)}
\newcommand{\OneFour}[4]{\left(\begin{array}{cccc} #1 & #2 & #3 & #4 \end{array} \right)}
\newcommand{\FourOne}[4]{\left(\begin{array}{c} #1 \\ #2 \\ #3 \\ #4 \end{array} \right)}
\newcommand{\Bra}[1]{\mathinner{\left\langle{#1}\right|}}
\newcommand{\Ket}[1]{\left|{#1}\right\rangle}
\newcommand{\KetBra}[2]{\Ket{#1}\!\Bra{#2}}
\newcommand{\matI}[0]{\TwoTwo{1}{0}{0}{1}}
\newcommand{\matX}[0]{\TwoTwo{0}{1}{1}{0}}
\newcommand{\matY}[0]{\TwoTwo{0}{-i}{i}{0}}
\newcommand{\matZ}[0]{\TwoTwo{1}{0}{0}{-1}}
こんにちは、@snuffkinです。
Webで量子コンピュータを紹介する文章を見ると、かなり確率で最適化問題に応用する話が挙げられています。しかし、この記事のテーマはその話とは違います。
量子コンピュータには古典コンピュータによる最適化が必要、という話です。
前提知識
密度行列やブロッホ球の扱いに慣れていないと読むのがツライかもしれません。少し説明しておきます。
定義(密度行列)
行列$\rho$が次の3つの条件をすべて満たすとき、密度行列という。
- $\rho$はエルミート行列。$\rho^\dagger = \rho$
- $\rho$のトレースは1。$\mathrm{Tr}[\rho]=1$
- $\rho$は半正定値。$\rho \geq 0$
通常は半正定値の定義にエルミート行列であることも含みますが、ここでは分けて書いています。
上記の定義に少し捕捉します。
エルミート行列の性質より、$\rho$の固有値は実数になります。
加えて、トレースが1なので、すべての固有値の和が1になります。
さらに、半正定値なので、どの固有値も0以上になります。
量子コンピュータで量子ビットの状態を表す方法はいくつかあり、よく見かけるのは状態ベクトルだと思います。ブラケット記法で、$\Ket{\psi} = \frac{1}{\sqrt{2}}(\Ket{0} + \Ket{1})$のように表すやつですね。
状態ベクトル$\Ket{\psi}$に対応する密度行列は$\KetBra{\psi}{\psi}$になります。
たとえば、$\Ket{\psi} = \Ket{0} = \TwoOne{1}{0}$のときに$\KetBra{\psi}{\psi}$を計算すると、
\begin{align}
\KetBra{\psi}{\psi} &= \TwoOne{1}{0}\TwoOne{1}{0}^\dagger \\
&= \TwoOne{1}{0}\OneTwo{1}{0} \\
&= \TwoTwo{1}{0}{0}{0} \\
\end{align}
となります。
念のため、密度行列の定義を満たしていることをチェックしておきましょう。
エルミート行列であること
$\TwoTwo{1}{0}{0}{0}^\dagger = \TwoTwo{1}{0}{0}{0}$
→OK
トレースが1であること
$\mathrm{Tr}\left[\TwoTwo{1}{0}{0}{0}\right] = 1 + 0 = 1$
→OK
半正定値であること
$\TwoTwo{1}{0}{0}{0}$は対角行列なので、対角成分が固有値になります。固有値は$1$と$0$なので、どの固有値も0以上です。
→OK
これで、確かに密度行列になっていることを確かめられました。
1量子ビットの場合、状態ベクトルは$2^n$次元ベクトルになりますが、密度行列は$2^n\times 2^n$次行列になります。
「ベクトルから行列になって、計算しづらいじゃないか」と思う方もいらっしゃると思いますが、密度行列の形で扱った方がよいこともいろいろあります。
良い性質1. 1量子ビットの密度行列はパウリ行列(と単位行列)の実数係数の線形結合で書ける
パウリ行列には、$X,Y,Z$の3種類があり、単位行列とパウリ行列は次のようなものです。
$$I=\matI, X=\matX, Y=\matY, Z=\matZ$$
たとえば、$\Ket{0}\Bra{0} = \TwoTwo{1}{0}{0}{0}$は次のように書けます。
\begin{align}
\TwoTwo{1}{0}{0}{0} &= \color{red}{\frac{1}{2}}\cdot\matI + \color{red}{0}\cdot\matX + \color{red}{0}\cdot\matY + \color{red}{\frac{1}{2}}\cdot\matZ \\
&= \color{red}{\frac{1}{2}}\cdot I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{\frac{1}{2}}\cdot Z \\
\end{align}
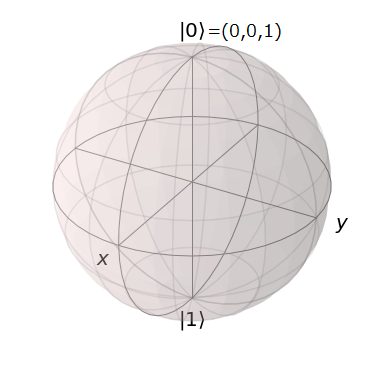
良い性質2. 線形結合の係数の2倍がブロッホ球の座標に対応する
密度行列が$\rho=\frac{1}{2}(I+xX+yY+zZ)$と書ける場合、ブロッホ球での座標は$(x,y,z)$になります。
たとえば、$\KetBra{0}{0} = \TwoTwo{1}{0}{0}{0}$は次のように書けます。
$$\KetBra{0}{0} = \TwoTwo{1}{0}{0}{0} = \frac{1}{2}(I + \color{red}{0}\cdot X + \color{red}{0}\cdot Y + \color{red}{1}\cdot Z) $$
そのため、$\Ket{0}$のブロッホ球での座標は$(0,0,1)$になります。
これらを踏まえて、本題に入りましょう。
その量子コンピュータは意図したとおりに動作していますか?
初期状態$\Ket{0}$を準備します。
量子コンピュータが意図したとおりに動いていれば、測定(細かく言うと$Z$測定)したときに高確率で$0$が返ってきます。もちろん、実機を使った場合は誤りがつきものなので、数%くらいは$1$が返ってくるかもしれません。
でも、10%とか20%とか1が返ってきたらどうでしょうか?
この場合は、量子コンピュータが意図したとおりに動作していない可能性があります。
クラウドから普通に量子コンピュータを使うとき、さすがにこういうことは起きないでしょう。
しかし、次のようなケースでは意図したとおりに動作しているか確認したくなります。
- 量子コンピュータのデバイスを開発したときに、動作確認する
- クラウド公開されている量子コンピュータを、OpenPulseを使って低レイヤで操作する
- 量子コンピュータとクマムシがエンタングルしてるか確認したい
- など...
こういうとき、どう間違ったのか把握するために、量子状態のパラメータがどうなっているか知りたくなります。そこで使われるのが量子状態トモグラフィという技術です。
量子状態トモグラフィって何ですか?
「量子状態」はここまでに何度も登場したので、大丈夫ですね。ベクトルの形式より密度行列の方が情報が多く、良い性質もあるので、密度行列のパラメータを知りたいです。
では、「トモグラフィ」とは何でしょうか。
Wikipediaには「物理探査、医療診断等で用いられる逆解析技術の一つ。日本語訳は、断層映像法または断層影像法である。」と書いてあります。何やら数式がたくさん並んでいますね。
一般的にも言葉が知られているトモグラフィだと、CTスキャンがあります。病院とかにあるやつで、多くの方向から人体をX線撮影することで、内部の立体的な情報を構成し、がん細胞の位置を特定する等に使われます。
ちなみに、CTスキャンは"Computed Tomography Scan"の略です。
トモグラフィを標語的に言うと、複数の方向から対象を測定し、測定結果から対象の状態を計算する手法という感じでしょうか。
これを踏まえて量子状態トモグラフィを標語的に言うと、測定結果から量子状態を計算(推定)する技術です。
カッコ書きで「推定」と書いたのは理由があります。量子力学では測定結果は確率的にしか分からないので、確率が高い量子状態を推定する手法だからです(完全に正確な量子状態は、普通は分かりません)。
素朴な量子状態トモグラフィ
量子状態が$\rho = \KetBra{0}{0} = \TwoTwo{1}{0}{0}{0}$であることを知らない前提で、密度行列のパラメータを推定するにはどうすれば良いでしょうか。
「前提」の節で紹介した密度行列の良い性質の2番目が使えます。
密度行列が$\rho = \frac{1}{2}(I+xX+yY+zZ)$と書けた場合、ブロッホ球での座標は$(x,y,z)$になりました。何度も量子状態を作り、$X$軸・$Y$軸・$Z$軸に沿って測定し、それぞれの期待値を求めれば$(x,y,z)$を推定できます。
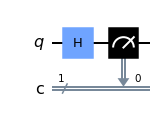
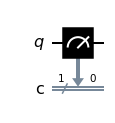
これらは$X$測定・$Y$測定・$Z$測定というもので、Qiskitの場合は量子回路の最後で次のような操作を行って測定できます。
$Y$測定($S^\dagger$ゲートと$H$ゲートをかけてから測定)
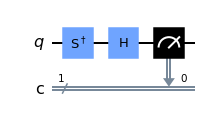
Qiskitには直接$X$測定や$Y$測定を行う命令がないため、ゲート操作で回転させてから測定する必要があります。
$0$を測定した回数をショット数で割れば、$0$を測定した確率が分かります。確率は0から1の値で、期待値は-1から1の値なので、「2 × 確率 - 1」を計算すれば確率を期待値に変換できます。
期待値(=ブロッホ球の$(x,y,z)$座標)が分かれば、密度行列$\rho$のパラメータが分かります。
これをQiskitでプログラミングすると次のようになります。
import numpy as np
from qiskit import QuantumCircuit, Aer, execute
# |0>を測定した回数を返す関数
def calc_count(circuit, backend = Aer.get_backend('qasm_simulator'), shots = 1000):
job = execute(circuit, backend, shots=shots)
return job.result().get_counts(circuit)["0"]
# 測定回数とショット数から、ブロッホ球の座標を求める関数
def count_to_coordinate(count, shots = 1000):
return 2 * (count / shots) - 1
# 推定する量子状態を準備
circuit = QuantumCircuit(1, 1)
# X測定
circuit_x = circuit.copy()
circuit_x.h(0)
circuit_x.measure(0, 0)
counts_x = calc_count(circuit_x)
coord_x = count_to_coordinate(counts_x)
print(f"count of x={counts_x}, coordinate of x={coord_x}")
# Y測定
circuit_y = circuit.copy()
circuit_y.sdg(0)
circuit_y.h(0)
circuit_y.measure(0, 0)
counts_y = calc_count(circuit_y)
coord_y = count_to_coordinate(counts_y)
print(f"count of y={counts_y}, coordinate of y={coord_y}")
# Z測定
circuit_z = circuit.copy()
circuit_z.measure(0, 0)
counts_z = calc_count(circuit_z)
coord_z = count_to_coordinate(counts_z)
print(f"count of z={counts_z}, coordinate of z={coord_z}")
I = np.array([[1, 0], [0, 1]])
X = np.array([[0, 1], [1, 0]])
Y = np.array([[0, -1j], [1j, 0]])
Z = np.array([[1, 0], [0, -1]])
rho = 1/2 * (I + coord_x * X + coord_y * Y + coord_z * Z)
print(f"density matrix=\n{rho}")
このプログラムを実行すると次のようになりました。
count of x=518, coordinate of x=0.03600000000000003
count of y=480, coordinate of y=-0.040000000000000036
count of z=1000, coordinate of z=1.0
density matrix=
[[1. +0.j 0.018+0.02j]
[0.018-0.02j 0. +0.j ]]
ここでは、シミュレータを使って各測定を1000ショットずつ実行しました。測定結果は確率的に得られるため、実行するたびにパラメータの値は多少変動します。
重要なのは出力の最後にある「density matrix=」の所です。これによると、密度行列は
$$\rho = \TwoTwo{1}{0.018+0.02i}{0.018-0.02i}{0}$$
と推定できました。
素朴に量子状態トモグラフィを行うと、このように推定できました。
この結果、おかしいぞ。。。
念のため、$\rho$が密度行列になっているか確認してみましょう。
エルミート行列であること
$\TwoTwo{1}{0.018+0.02i}{0.018-0.02i}{0}^\dagger = \TwoTwo{1}{0.018+0.02i}{0.018-0.02i}{0}$
→OK
トレースが1であること
$\mathrm{Tr}\left[\TwoTwo{1}{0.018+0.02i}{0.018-0.02i}{0}\right] = 1 + 0 = 1$
→OK
半正定値であること
手計算は面倒ですね。numpyに固有値を求める関数があるので、それを使いましょう。
次のプログラムを実行すれば、固有値が分かります。
eigvals, eigvecs = np.linalg.eigh(rho)
print(eigvals)
実行すると次の結果になりました。
[-0.000723 1.000723]
固有値の和は1になっていますが、-0.000723という負の固有値が出てきましたね。
これでは、密度行列の定義を満たしませんね。
ブロッホ球の中心からの距離$\sqrt{x^2 + y^2 + z^2}$も求めてみましょう。密度行列の定義を満たしていれば、ブロッホ球の表面か内側に位置するはずなので、この距離は1以下になります。
distance = np.sqrt(coord_x ** 2 + coord_y ** 2 + coord_z ** 2)
print(distance)
実行すると次の結果になりました。
1.0014469531632717
1を越えました。。。
ということは、この密度行列(?)はプロッホ球の外側に位置しています。物理的(量子力学的)にあり得ない密度行列(?)になってしまいました。
やはり、この結果、おかしいぞ。。。
測定結果が確率的に得られるため、こういうことが起きてしまいます。純粋状態は物理的に許される状態とあり得ない状態の境界線上にあるため、こういう結果になりやすいです。
そのため、物理的に許される密度行列を計算するには、制約(密度行列の定義)を満たした上で推定する必要があります。
古典コンピュータによる最適化
そこで登場するのが、制約付き最適化です。(ようやく本題です)
制約付き最適化は、制約を満たしたものの中で最適なものを求める手法です。
$\rho_{\text{est}}$を推定(最適化)の結果とし、$\rho_{\text{empi}}$を素朴な量子状態トモグラフィで求めた密度行列とします。("est"はestimate、"empi"はempirical distributionを意図しています)
たとえば、最小二乗法を使って物理的に許される密度行列を求めるには、次の最適化を行います。(通常は半正定値の定義にエルミート行列であることも含みますが、ここでは分けて書いています)
\begin{array}{cc}
\text{minimize} & ||\rho_{\text{est}} - \rho_{\text{empi}}||_{2} \\
\text{subject to} & \rho_{\text{est}}^\dagger = \rho_{\text{est}}, \\
& \mathrm{Tr}[\rho_{\text{est}}]=1, \\
& \rho_{\text{est}} \geq 0. \\
\end{array}
この式は、密度行列の定義を満たすもので、$\rho_{\text{empi}}$に一番近いものを求めることを意味しています。
たとえばQiskitには量子状態トモグラフィを行うライブラリがあり、
- CVXPYを利用した凸最適化(密度行列全体は凸集合になります)
- SciPyを利用した最小二乗法
から最適化手法を選択できます。
このように、最適化を行うことで物理的に許される密度行列を推定することができます。
また、量子状態トモグラフィ以外にも、推定対象を量子ゲートからなる量子プロセスにした量子プロセストモグラフィや、推定対象をPOVMにしたPOVMトモグラフィ等、様々な種類があります。これらをまとめて量子トモグラフィといいます。
というわけで、この話をまとめると、
- 量子コンピュータで作った量子状態を確認するには量子状態トモグラフィが必要で、
- 物理的に許される量子状態を推定するには古典コンピュータによる最適化が必要
となります。
量子コンピュータには古典コンピュータによる最適化が必要、という量子状態トモグラフィの紹介でした。
参考文献
いずれも日本語で読める量子トモグラフィの入門資料で、オススメです。
- 「大規模量子計算機の実用化における統計的問題」(杉山太香典)
https://repository.kulib.kyoto-u.ac.jp/dspace/handle/2433/231709 - Qiskitチュートリアル「量子トモグラフィー」
https://qiskit.org/documentation/locale/ja_JP/tutorials/noise/8_tomography.html