こんにちは.U-TOKYO AP Advent Calendar 2018 10日目の担当のsnowhorkです.
この記事は,確率的勾配降下法の理論入門の定理証明編です.
証明する定理
パラメーター$w$におけるデータ$(x_i, y_i)$に関する損失関数を$l_i(w)$とします.
損失関数のデータの分布に関する期待値$L(w)=\mathbb{E}_{x_i, y_i}(l_i(w))$を汎化誤差といいます.
$l_i(w)$が$a-$平滑な凸関数で,非負な損失関数である時,
\mathbb{E}[L(\overline{w})]\leq \frac{1}{1-\eta a}(L(w^*) + \frac{{w^*}^2}{2\eta T}) \tag{1}
が成り立ちます.
この定理はSGDによって得られるパラメーター$\overline{w}$による汎化誤差と,最も良いパラメーターを用いた汎化誤差とのずれについての評価です.$\frac{1}{1-\eta a}$倍のずれで$O(1/T)$で収束していくということがわかります.
本項ではこれを証明したいと思います.
準備
あらためて凸関数や平滑関数の定義を紹介して,性質を紹介したいと思います.
凸関数
凸関数とは,グラフ上の2点で線分を引くと,それより下にグラフがくるような関数です.
凸関数の例
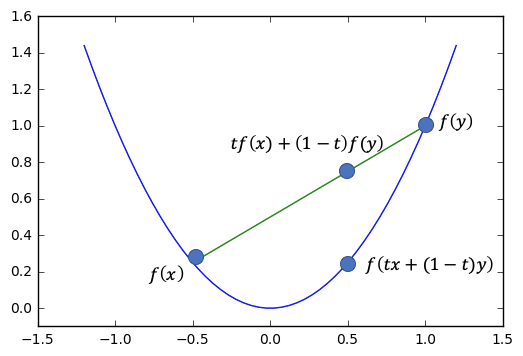
上の例では,グラフ上の2点で緑の線分を引くと,青のグラフが必ず下にきます.
凸関数の定義
関数fが凸関数であるとは,
f上の2点(x,f(x)), (y, f(y))と,\\
それらの間の点(tx + (1-t)y), f(tx + (1-t)y)) について,\\
f(tx + (1-t)y) \leq tf(x) + (1-t)f(y) が成立することです.
凸関数の性質1
$f$が微分可能な凸関数の時,その勾配$f'(w)$について,全ての$w^*$について,
f(w) - f(w^*) \leq f'(w)(w-w^*) \tag{2}
が成り立ちます.
凸関数の場合,勾配は単調増加するので,
\frac{f(w) - f(w^*)}{w-w^*} \leq f'(w) \ \ \ (w^* < w のとき)
が成り立ちます.$(w^* > w)$の場合も同様です.
凸関数の性質2
損失関数$l_i$が凸関数の時,$w_i$ と$\overline{w} = \frac{\sum_{i=1}^T w_i}{T}$について,
L(\overline{w}) \leq \frac{1}{T}\sum_i{L(w_i)} \tag{3}
が成り立ちます.
(証明)
$l_i$が凸関数なので,
l_i(\overline{w}) \leq \frac{1}{T}\sum_i{l_i(w_i)}
が成り立ちます.両辺を$x_i,y_i$について期待値を取れば,目的の式が得られます.(証明終)
この式を見れば,SGDにおいて各$w_i$を用いるよりは平均した$\overline{w}$を用いる方が期待値の意味で良いということがわかります.
平滑関数
今回考えている二乗損失の関数は平滑性があり,良い性質が成り立ちます.
平滑関数の定義
微分可能な関数f(w)がa-平滑関数であるとは, \\
|f'(w) - f'(u)|\leq a|w-u| \ が成立することです.
平滑関数の性質
微分可能な関数f(w)がa-平滑関数であるとき,
f(v)\leq f(w) + (v-w)f'(w) + \frac{a}{2} (v-w)^2
が成り立ちます.
(証明)
平滑関数の性質を用いるために,$f'(w+t(v-w))-f'(w)$を評価します.ただし,$t\in[0,1]$です.
f'(w+t(v-w))-f'(w) \leq |f'(w+t(v-w))-f'(w)| \\
\leq a|w+t(v-w))-w| = at|v-w|
1行目から2行目において,平滑関数の性質を用いました.
両辺を$t$について[0,1]で積分します.
\int_{[0,1]}(f'(w+t(v-w))-f'(w))dt \leq \int_{[0,1]} at|v-w|dt
まず右辺は,
\int_{[0,1]}at|v-w| dt = \frac{a}{2}|v-w|
となります.次に左辺は,
\int_{[0,1]}(f'(w+t(v-w))-f'(w)) dt = \frac{f(v) - f(w)}{v-w}-f'(w)
これらを代入すると,
\frac{f(v) - f(w)}{v-w}-f'(w) \leq \frac{a}{2}|v-w|
$v>w$の時と,$v<w$の場合で場合分けが必要ですが,移項をすると目的の式が得られます.(証明終)
非負平滑関数の性質
$f$が非負であるとします.上の式で$v = w - \frac{1}{a}f'(w)$ ととることで,
f(v)\leq f(w) + (- \frac{1}{a}f'(w))f'(w) + \frac{a}{2} (- \frac{1}{a}f'(w))^2 \\
= f(w) - \frac{1}{2a} (f'(w))^2 \\
(f'(w))^2 \leq 2a(f(w) - f(v)) \leq 2af(w) \tag{4}
が成り立ちます.最後の不等式で$f$が非負であることを使いました.
SGD
SGDのアルゴリズムを再掲します.
- $\eta$ を設定
- $w_1=0$ で初期化
- ステップ$i=1,2,\dots,T$で以下を繰り返す
- $(x_i, y_i)$ をサンプル
- $w_{i+1} = w_i - \eta l_i'{(w_i)}$ で更新
- $\overline{w} = \frac{\sum_i w_i}{T}$ を出力
SGDの性質
(SGDに限らず),次のようにパラメーターを更新するとします.
w_1=0, w_{i+1} = w_{i} - \eta v_{i}
このとき,全ての$w^*$について,
\sum_{i=1}^T (w_i-w^*)i_t \leq \frac{|w^*|^2}{2\eta} + \frac\eta 2 \sum_{i=1}^T |v_i|^2
が成り立ちます.特に,SGDの場合は,$v_i = l'(w_i)$なので,
\sum_{i=1}^T (w_i-w^*)l'(w_i) \leq \frac{|w^*|^2}{2\eta} + \frac\eta 2 \sum_{i=1}^T |l'(w_i)|^2 \tag{5}
が成り立ちます.
(証明)
今のステップと前のステップとの二乗差$(w_{i+1}-w^*)^2-(w_i-w^*)^2$を比較するところが証明のポイントです.
更新式$w_{i+1} = w_i - \eta v_{i}$を使うことができます.
(w_{i+1}-w^*)^2-(w_i-w^*)^2 = (w_i - \eta v_{i}-w^*)^2-(w_i-w^*)^2 \\
= -2\eta v_{i}(w_i-w^*) + (\eta v_{i})^2
両辺について$i$に関して和を取ります.
(w_{T+1}-w^*)^2-(w_1-w^*)^2 = -2\eta \sum_{i=1}^T v_{i}(w_i-w^*) + \sum_{i=1}^T (\eta v_{i})^2
移項して評価すると,
2\eta \sum_{i=1}^T v_{i}(w_i-w^*) \leq -(w_{T+1}-w^*)^2+(w_1-w^*)^2 + \sum_{i=1}^T (\eta v_{i})^2 \\
\leq (w_1-w^*)^2 + \sum_{i=1}^T (\eta v_{i})^2 \\
\leq (w^*)^2 + \sum_{i=1}^T (\eta v_{i})^2
最後に$w_1=0$を代入しました.両辺を$2\eta$で割ると,目的の式が得られます.(証明終)
定理の証明
ここまででてきた凸関数の性質,平滑関数の性質,SGDの性質を全て組み合わせていくと目的の式(1)を証明することができます.
((1)の証明)
まずはSGDの性質$(5)$を用います.
\sum_{i=1}^T (w_i-w^*)l'(w_i) \leq \frac{|w^*|^2}{2\eta} + \frac\eta 2 \sum_{i=1}^T |l'(w_i)|^2 \tag{5}
左辺の$(w_i-w^*)l'(w_i)$に注目して,凸関数の性質$(2)$を適用します.
\sum_{i=1}^T (l_i(w_i)-l_i(w^*)) \leq \frac{|w^*|^2}{2\eta} + \frac\eta 2 \sum_{i=1}^T |l'(w_i)|^2
右辺の$|l'(w_i)|^2$に注目して,非負平滑関数の性質$(4)$を適用します.
\sum_{i=1}^T (l_i(w_i)-l_i(w^*)) \leq \frac{|w^*|^2}{2\eta} + \frac\eta 2 \sum_{i=1}^T (2a)l(w_i) \\
= \frac{|w^*|^2}{2\eta} + \eta a \sum_{i=1}^T l(w_i)
移項して整理します.
(1-\eta a)\sum_{i=1}^T l_i(w_i) \leq
\sum_{i=1}^T l_i(w^*) + \frac{|w^*|^2}{2\eta}
両辺を$T$で割ります.
(1-\eta a)\frac{\sum_{i=1}^T l_i(w_i)}{T} \leq
\frac{\sum_{i=1}^T l_i(w^*)}{ T } + \frac{|w^*|^2}{2\eta T}
両辺の期待値を取ります.$\sum_{i=1}^T l_i(w^*)=TL(w^*)$となります.
(1-\eta a)\frac{\sum_{i=1}^T L(w_i)}{T} \leq
\frac{TL(w^*)}{ T } + \frac{|w^*|^2}{2\eta T} = L(w^*) + \frac{|w^*|^2}{2\eta T}
最後に,凸関数の性質$(3) L(\overline{w}) \leq \frac{1}{T}\sum_i{L(w_i)}$を左辺に適用します.
(1-\eta a)L(\overline{w}) \leq L(w^*) + \frac{|w^*|^2}{2\eta T}
両辺を$1- \eta a$でわると,目的の式が得られます.お疲れ様でした! ![]()
![]()
まとめ
確率的勾配法は深い理論があり,その有効性が今でも研究されています.(最も簡単な例でも結構大変ですね...)
今回は簡単のためパラメーター$w$は1次元としましたが,多次元のパラメーターの場合でも全く同様に成立します.
最後に参考文献を挙げておきます.
鈴木大慈 『確率的最適化』
和書ですが,やや一般的・形式的な書き方がされているため,初学者には難しいかもしれません.
S. Shalev-Shwartz, S. Ben-David 『Understanding Machine Learning: From Theory to Algorithms』
洋書ですが,内容自体は初学者にもわかりやすいです.
U-TOKYO AP Advent Calendar 2018 はまだまだ続きます!
