確率的勾配降下法の理論入門（実験編）

機械学習のパラメーター学習，特にニューラルネットワークの学習をするときには，確率的勾配降下法（SGD)の理解は欠かせません．アルゴリズム自体の解説は日本語でも多くありますし，多くの深層学習フレームワークではSGDを簡単に実装できます．

この記事ではSGDの理論について焦点を当てます．SGDの理論では，どれくらいのスピードで最適解に近づいていくかを数式で解析していきます．この記事ではSGDの理論的側面の基礎について解説して，プログラミングによる実験で，その理論の当てはまりを確認していこうと思います．

今回考える問題

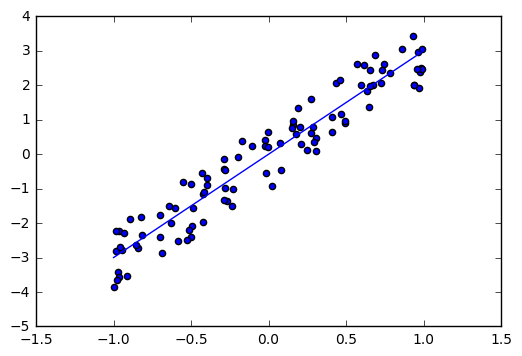
1変数の線形回帰を考えます．真の直線は$y=3x$ですが，そこにノイズがいくらか乗って，サンプルされる状況を考えます．
サンプルから，真の傾き3を推定する問題を考えていきます．

import numpy as np
from scipy.stats import truncnorm
import matplotlib.pyplot as plt

true_w = 3.0
beta = 1.0
sigma = 1.0

def sample():    
    x = np.random.uniform(-beta,beta)
    e = np.random.normal(0.0, sigma)
 
    y = true_w*x+e
    return x,y

samples = [sample() for _ in range(100)]
plt.scatter([sample[0] for sample in samples], [sample[1] for sample in samples])
plt.plot(np.linspace(-1,1), [x*true_w for x in np.linspace(-1,1)])
plt.show()

形式的に書くと，以下のような設定を考え，$w^* = 3$を推定します．

x \sim U[-1, 1], \\
\epsilon \sim N(0, 1),  \\
y = w^*x+\epsilon, w^* = 3 \\

損失関数

$w^* =3$　は未知であり，$w$をできるだけ$w^*$に近づけていくことを考えます．
線形回帰では二乗誤差を損失関数とします．$i$回目のサンプルを$(x_i, y_i)$として，その損失関数は，

l_i(w) = \frac 1 2 (wx_i - y_i)^2

と書くことができます．

SGDを用いるにはその勾配が必要になります．微分することで勾配は，

l_i^´(w) = (wx_i - y_i)x_i

で表されます．

def loss(w, x, y):
    return (w*x-y)**2

def w_grad(w, x, y):
    return 2*(w*x - y)*x

確率的勾配降下法(SGD)

SGDのアルゴリズムは以下のようになります．

• $\eta$ を設定
• $w_1=0$ で初期化
• ステップ$i=1,2,\dots,T$で以下を繰り返す
  • $(x_i, y_i)$ をサンプル
  • $w_{i+1} = w_i - \eta l_i'{(w_i)}$ で更新
• $\overline{w} = \frac{\sum_i w_i}{T}$ を出力

接戦の方向にパラメーターを変更していくのは，いわゆる普通の勾配法（最急降下法）と同じなのですが，$(x_i, y_i)$が確率的にサンプリングされるところが普通の勾配法とは異なる点です．

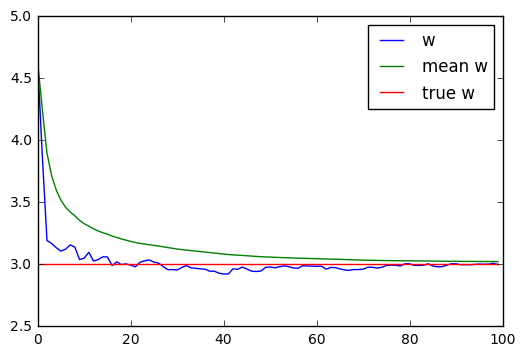
$(x_i, y_i)$はノイズを含むので各$w_i$は振動するのですが，その平均をとることで滑らかにしています．

以下の図は実験の一例です．青の線が各$w_i$で，緑の線がそのステップでの平均になります．平均が滑らかに真の値に収束していくことがわかります．

SGDの理論

SGDの理論を学ぶためには，凸関数の性質の理解が欠かせません．
まずは凸関数の性質について簡単に紹介したいと思います．

凸関数

凸関数とは，グラフ上の２点で線分を引くと，それより下にグラフがくるような関数です．
凸関数の例

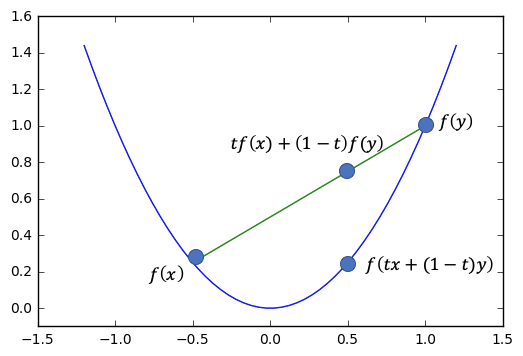
上の例では，グラフ上の２点で緑の線分を引くと，青のグラフが必ず下にきます．

形式的に書くと，次のようになります

関数fが凸関数であるとは，

f上の２点(x,f(x)),　(y, f(y))と，\\
それらの間の点(tx + (1-t)y), f(tx + (1-t)y)) について，\\
f(tx + (1-t)y) \leq tf(x) + (1-t)f(y) が成立することです．

今回の問題で考えているような，二乗損失も二次関数の形であり，凸関数であるといえます．

平滑関数

今回考えている二乗損失は，凸関数であるだけでなく，微分可能であり平滑という特徴も持っています．

微分可能な関数f(w)がa-平滑関数であるとは， 　\\
|f'(w) - f'(u)|\leq a|w-u| \ が成立することです．

例えば，$f(w)=\frac{1}{2}w^2$ は1-平滑関数です．なぜなら，

|f'(w) - f'(u)| = |w - u|

が成立するからです．

今回の損失関数$l_i(w) = \frac 1 2 (wx_i - y_i)^2$は，$l_i^´(w) = (wx_i - y_i)x_i$であるので，

|l_i^´(w)-l_i^´(u)| = |(wx_i - y_i)x_i - (ux_i - y_i)x_i| \\
= |wx_i^2 -y_ix_i - ux_i^2 + y_ix_i| \\
= |wx_i^2 - ux_i^2| \\
= |x_i^2||w-u| \\
\leq |w-u|

が成り立ちます．$x_i$は$[-1,1]$の範囲にしか値を取らないことを使いました．よって，　$l_i$は1-平滑関数です．

SGDの誤差に関する定理

損失関数の期待値を$L$とします．

L(w)= \mathbb{E}_{x_i, y_i}l_i(w) = \mathbb{E}_{x_i, y_i}\frac{1}{2}(x_iw-y_i)^2 \\
= \mathbb{E}_{x_i, \epsilon}\frac{1}{2}(x_iw-(x_iw^*+\epsilon))^2 \\
= \mathbb{E}_{x_i, \epsilon}\frac{1}{2}(x_i(w-w^*)+\epsilon))^2 \\
= \mathbb{E}_{x_i, \epsilon}\frac{1}{2}(x_i^2(w-w^*)^2+ x_i(w-w^*)\epsilon + \epsilon^2))

この$L$は汎化誤差とよばれます．真のパラメーター $w^*$ における汎化誤差 とSGDで得られるパラメーター$\overline{w}$における汎化誤差を比較します．

今回の設定では，

x \sim U[-1, 1], 
\epsilon \sim N(0, 1),  

であるので，

\mathbb{E}(x_i)=0, \mathbb{E}(\epsilon)=0　\\
\mathbb{E}(x_i^2)=\mathbb{E}(x_i)^2 + \mathbb{V}(x_i) = \frac{1}{3} \\
\mathbb{E}(\epsilon^2)=\mathbb{E}(\epsilon)^2 + \mathbb{V}(\epsilon)=1

が成立します．なお，$x \sim U[a, b]$の分散は$\frac{(b-a)^2}{12}$です．これらを$L(w)$の式に代入すると，

L(w)= \frac{1}{2}(\frac{1}{3}(w-w^*)^2+1)

が得られます．

この汎化誤差に関して，$l_i$が$a-$平滑な凸関数で非負な損失関数であるとき，

\mathbb{E}[L(\overline{w})]\leq \frac{1}{1-\eta a}(L(w^*) + \frac{{w^*}^2}{2\eta T})

が成立します．
証明は理論編に続きます．

定理の実証

まずは，SGDを実装してしまいます．

np.random.seed(77)

times = 100

loss_list = [[] for _ in range(times)]

eta = 0.25

for time in range(times):
    w = np.random.uniform(-1,1)
    w = 0
    w_list = []
    T = 50

    for t in range(1, T+1):
        x, y = sample()
        dw = w_grad(w, x, y)
        w = w - eta*dw
        w_list.append(w)

    for t in range(1, T+1):
        w = np.mean(w_list[:t])
        
        loss = 0.5*(((w-true_w)**2)*((beta*2)**2/12)+sigma)
        loss_list[time].append(loss)

$\mathbb{E}[L(\overline{w})]$は100回行なった平均で計算します．$\frac{1}{1-\eta a}(L(w^*) + \frac{{w^*}^2}{2\eta T})$は正確に計算します．

t_start = 5

Trange = range(t_start, T+1)

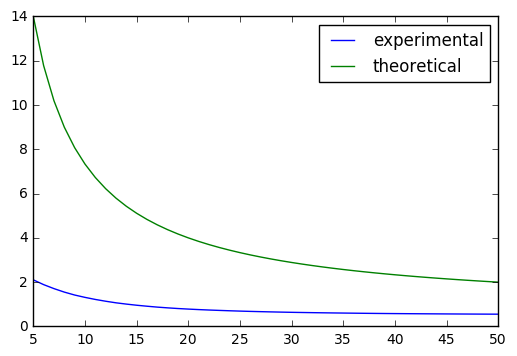
plt.plot(Trange, np.mean(loss_list, axis=0)[t_start-1:], label="experimental")
plt.plot(Trange, [(1.0/(1.0-eta*beta))*(0.5*sigma + (true_w**2)/(2*eta*t)) for t in Trange] , label="theoretically")

plt.legend()
plt.show()

実験結果をプロットしたものを下の図に示します．

緑の線が，定理における左辺で，青の線が定理における右辺になっています．確かに（左辺）$\leq$（右辺）が成立していることがわかります．（今回の実験は簡単な問題なので理論の上界よりも早く収束しているように見えます）

明日は上の定理を解説したいと思います！

追記：
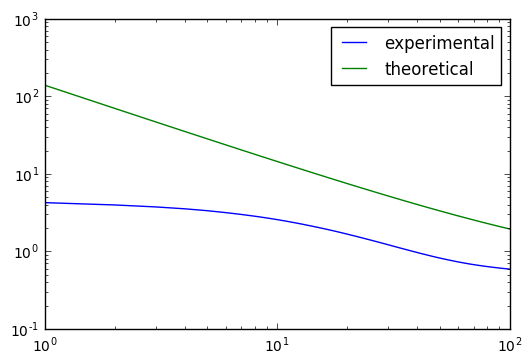
上のグラフに対して，両対数グラフをとったものを示します．

Tが大きい範囲では理論の場合と実験の場合で同じ傾きをしていることがわかります．
故に定数倍を除いてオーダーとしては等しいようにもみえます．