【機械学習入門】多項式フィッティング問題へのアプローチ（１）～最尤法～

#0. はじめに
昨今の機械学習ブームにあやかり、遅ばせながら統計学の勉強を始めました。
インプットばかりではどうしても理解が進まないので、備忘録もかねて、学習したことをまとめていこうと思います。

まずは、基本的な回帰(Regression)の問題である、多項式フィッティング問題を題材に、機械学習を学ぶ上で必要な確率モデル的な考え方の基礎について、複数回に分けて、解説していこうと思います。

筆者自身も理解が不十分な点もあるので、記載内容に誤りが含まれている可能性もございます。
**”コイツ意味不明なこと言ってるぞwww”**という箇所がありましたら、ご指摘頂けますと非常に助かります。
質問等も大歓迎ですので、何かありましたらコメント欄までお願いします。

#前提知識
１）大学の基本レベルの微分積分と線形代数の知識
２）基本的な確率の知識

#本記事の目標

１）多項式フィッティング問題とは何かを理解すること
２）最尤法とは何かを理解すること
３）最尤法と最小二乗法による解法の関係について理解すること

#1. 多項式フィッティング問題とは
多項式フィティング問題では、観測されたデータの背後に存在する関係式を、多項式(Polynomial)で推定することを考えます。

h(x;\boldsymbol{w})=w_{0}+w_{1}x+w_{2}x^{2}+\dotsb+w_{\mathrm{M}}x^{\mathrm{M}}=\sum_{j=0}^{\mathrm{M}}w_{j}x^{j}\\w_{j} \in \mathcal{R}\ \ (\ j=0,1,2,\cdots,\mathrm{M}\ )

$\mathrm{\small{M}}$ は多項式の次数(Degree)であり、次数が高くなるほど、より複雑なモデルを表現することが出来ます。
例えば、信号成分 $\ f(x)=\sin (2\pi x) $ からサンプリングしたデータ点に対し、多項式フィティングを行うと次のような結果になります。

　　　　　　　　　　　　　　　　　**図１: 多項式フィッティングの結果** 　　引用：Christoper M. Bishop (2006) *Pattern Recognition and Machine Learning* : Springer

上図において、青丸は観測データ、緑線は信号成分、赤線はフィッティング曲線を表しています。
$\mathrm{\small{M=0,1}}$ の場合は、モデルが単純過ぎるため、正弦波の曲線構造を捉えることが出来ていません。¹
一方で、 $\mathrm{\small{M=9}}$ の場合は、モデルが複雑過ぎるため、観測ノイズに過剰に反応してしまっています。²
$\mathrm{\small{M=3}}$ の場合は、フィッティングがうまくいっていると言えそうです。

この例からも分かる通り、多項式フィッティングを行う際には、次数 $\mathrm{\small{M}}$ の値を適切に選択する必要があります。
しかし、観測データを生成している分布が事前に分かっているケースは少ないので（むしろ、事前に分からないからこそ、フィッティングにより近似的に真の分布を求めようとしている）、次数の選択に関してはトライアンドエラーで適切な値を見つけることが必要になります。

次数の選択まで含めてモデル化する手法として、目的関数(Objective function)³に正則化項(Regularization term)⁴を追加する方法などが知られていますが、詳しくは別の記事にまとめようと思います。

以降は、既に適切な次数 $\mathrm{\small{M}}$ の選択が行われているという前提で議論を進めることにします。

#2. 問題の定式化
観測データが次の正弦波から生成されるとします。

\ f(x)=\sin (2\pi x) \quad  (0 \leqq x \leqq 1)

この時、正弦波に正規分布 $\mathcal{N}(0,\sigma^{\scriptsize{2}})$⁵ に従うサンプリングノイズ $\epsilon$ が乗った関数

\ g(x)=\sin (2\pi x)+\epsilon=\ f(x)+\epsilon \quad  (0 \leqq x \leqq 1)

を多項式で近似し、区間 $[0,1]$ 内で等間隔にサンプルされた $\mathrm{\small{N}}$ 個の観測データ $ \mathcal{D} = \{(x_n,g(x_n)) \}_{n=1\sim\ \mathrm{N}}$ を用いて信号成分 $\ f(x)$ を近似することを考えます。
$\mathrm{\small{M}}$ 次多項式による近似曲線は

h(x;\boldsymbol{w})=\displaystyle \sum_{j=0}^{\mathrm{M}}w_{{j}}x^{{j}}\\
\boldsymbol{w}=( w_0, w_1, w_2,\ldots, w_\mathrm{M} )^{\mathrm{T}} \in \mathcal{R^{\mathrm{M+1}}}\ 

と書けるので、観測データ $\mathcal{D}$ を用いて係数ベクトル $\boldsymbol{w}$ を決定することが、今回の目標となります。

#3. 解法アプローチ
フィッティング曲線を求めるための具体的な手法を紹介します。

アプローチとしては、直感的に分かりやすい最小二乗法(Least square method)⁶による解法と確率モデルを用いた最尤法(Maximum likelihood method)による解法の2パターンが広く知られています。

いずれの手法も同一の目的関数の最小化問題に帰着するため、結果として得られる近似曲線は同じになります。
しかし、前者の手法は往々にしてデータの誤差の構造に盲目的になりがちであり、実践的な手法とは言えません。

そこで今回は、確率モデルとして誤差の構造を数学的に議論することができる最尤法を紹介します。

###3-1. 最尤法とは
最尤法(Maximum likelihood method)は、尤度(Likelihood)と呼ばれる統計量の最大化により、母集団を表現するモデルに付随するパラメタを、観測データから点推定する手法です。

尤度は、想定したモデルの下で、観測データが生成される同時確率(Joint probability)のことであり、確率密度関数(Probability density function)⁷に付随するパラメタの関数として定義される統計量です。

即ち、最尤法は解釈するなれば、母集団に対してあるモデルを想定した時に、手元にある観測データが尤もらしいデータであると言えるような（実際に観測されたデータが発生する確率が、想定したモデルから生成され得る全ての他のデータの各発生確率よりも高いと言えるような）パラメタを選択する手法と理解できます。

それでは、最尤法を定式化してみましょう。

$( X_1, X_2, X_3,\ldots, X_\mathrm{n})$ を独立同分布(Independent and identically distributed)⁸に従う確率変数の組とし、その観測値が　$( x_1, x_2, x_3,\ldots, x_\mathrm{n})$ で与えられているとします。
更に、確率変数の結合確率密度関数(Joint probability density function)の関数形を $\ {f}$ として、付随するパラメタを $\theta$ とすれば、最尤法の定式化は以下の様になります。

\theta_{ML} =\mathrm{argmax}_{\theta} \ {f(x_1,x_2,\ldots,x_\mathrm{n};\theta)}=
\mathrm{argmax}_{\theta} \ \displaystyle \prod_{ i = 1 }^n f(x_i;\theta)

$\theta_{ML}$ はパラメタ $\theta$ の最尤推定値(Maximum likelihood estimate)と呼ばれます。
上式の３項目は、確率変数が独立同分布であるという仮定から従う式変形に過ぎないことに注意してください。
結合確率密度関数のパラメタに関する最大化こそが最尤法の本質です。

一般に、尤度の最大化を考える際には、尤度を対数変換し、対数尤度(Log likelihood)の最大化として問題を定式化する場合が多いです。
実際、対数は単調増加関数なので、尤度の最大化を対数尤度の最大化に置き換えることに問題はありません。

\theta_{ML} =
\mathrm{argmax}_{\theta} \ \log(\displaystyle \prod_{ i = 1 }^n \ f(x_i;\theta)) =
\mathrm{argmax}_{\theta} \ \displaystyle \sum_{ i = 1 }^n \ \log(\ f(x_i;\theta))

対数尤度を導入したことにより、確率密度関数の積を和に書き直すことが出来ました。

対数尤度を最大化するパラメタを求めるための手続きとしては、

１）対数尤度をパラメタに関して偏微分し、偏微分係数の値が０になるパラメタを代数的に求める。
２）対数尤度をパラメタに関して偏微分し、偏微分係数の値が０になるパラメタをNewton-Raphson法などのアルゴリズムを用いて数値計算的に求める。

などが考えられます。

###3-2. 最尤法による多項式フィティング問題の解法
それでは、最尤法による多項式フィッティング問題の解法を解説して行きます。

問題設定をおさらいしておくと、今回の観測データ $ \mathcal{D} = \{(x_n,g(x_n)) \}_{n=1\sim\ \mathrm{N}}$ は、正弦波に正規分布 $\mathcal{N}(0,\sigma^{\scriptsize{2}})$ に従うサンプリングノイズ $\epsilon$ が乗った確率変数として得られたものでした。

\ g(x)=\sin (2\pi x)+\epsilon=\ f(x)+\epsilon \quad  (0 \leqq x \leqq 1)

さて、最尤法の枠組で考えるためには、確率変数の結合確率密度関数が必要になりますが、まずは各観測データ点の確率密度関数について考えてみましょう。

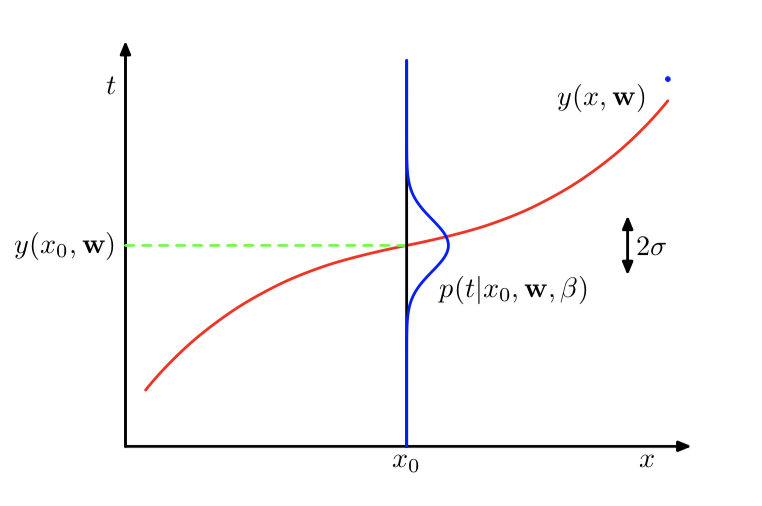**図２：確率変数としての観測データ点の生成過程** 引用：Christoper M. Bishop (2006) *Pattern Recognition and Machine Learning* : Springer

$n$ 番目のデータ点は、平均が $n$ 番目のサンプリング点における信号成分 $ \ f(x_n)$ 、分散がサンプリングノイズの分散 $\sigma^{\scriptsize{2}}$ の正規分布 $\mathcal{N}(\ f(x_n),\sigma^{\scriptsize{2}})$ に従って生成されます。
今回は信号成分 $ \ f(x)$ を $\mathrm{\small{M}}$ 次多項式 $ \ h(x;\boldsymbol{w})$ で近似することを考えているので、$\mathcal{N}(\ h(x_n;\boldsymbol{w}),\sigma^{\scriptsize{2}})$ と置き換えて、これを $n$ 番目のデータ点の（近似）確率密度関数と考えます。

ここで、各データ点は独立同分布であることに注意すれば、結合確率密度関数は各店の確率密度関数の積で書けるので、尤度 $L$ は以下のように書けます。

L=\displaystyle \prod_{ n = 1 }^{\mathrm{N}}   \mathcal{N}(\ g(x_n);h(x_n;\boldsymbol{w}),\sigma^{\scriptsize{2}}))

対数を取れば、対数尤度 $l$ は、

l=\displaystyle \sum_{ n = 1 }^{\mathrm{N}}  \log (\mathcal{N}(\ g(x_n);h(x_n;\boldsymbol{w}),\sigma^{\scriptsize{2}}))

となります。

ここで、平均 $\mu$、分散 $\sigma^2$ の正規分布の確率密度関数は

\mathcal{N}(x ;\mu,\sigma^{\scriptsize{2}})=\frac{1}{\sqrt{2\pi}\sigma}\exp\left (-\frac{(x-\mu)^2}{2\sigma^2}\right )

なので、対数尤度を陽に書くと

l=\displaystyle \sum_{ n = 1 }^{\mathrm{N}}  \log \left (\left (\frac{1}{2\pi\sigma^2}\right )^{\frac{\mathrm{N}}{2}}\exp\left (-\frac{(g(x_n)-h(x_n;\boldsymbol{w}))^2}{2\sigma^2}\right )\right )=\frac{\mathrm{N}}{2}\log\left (\frac{1}{2\pi}\right )-\mathrm{N}\log \sigma -\displaystyle \sum_{ n = 1 }^{\mathrm{N}}  \frac{(g(x_n)-h(x_n;\boldsymbol{w}))^2}{2\sigma^2}

が得られます。

さて、対数尤度を具体的に書き下すことが出来たので、あとは各パラメタの関数だと思って、対数尤度を最大化するようなパラメタを、それぞれ求めれば良いことになります。

特に、パラメタ $ \boldsymbol{w}$ に関する最大化は、第３項の最小化と同値なので、

\boldsymbol{w}_{ML}=\mathrm{argmin}_{\ \boldsymbol{w}}\displaystyle \sum_{ n = 1 }^{\mathrm{N}}  \left (g(x_n)-h(x_n;\boldsymbol{w})\right )^2

となり、最小二乗法と同様に、二乗和誤差(Mean squared error)の最小化問題に帰着出来ることが分かります。

$\sigma$ に関する最大化は、偏微分の値を０とすれば、

\sigma_{ML}=\sqrt{\frac{2}{\mathrm{N}}\displaystyle \sum_{ n = 1 }^{\mathrm{N}}  \left (g(x_n)-h(x_n;\boldsymbol{w})\right )^2} \simeq \frac{1}{\mathrm{N}}\displaystyle \sum_{ n = 1 }^{\mathrm{N}}  \left (g(x_n)-h(x_n;\boldsymbol{w})\right )^2

となり、更に平方根を展開すると、仮定したサンプリングノイズの値が二乗和誤差で近似できることが分かります。

###3-3. 最小二乗法との関係
最尤法による解法が最小二乗法による解法と同一の目的関数の最小化問題に帰着できることを見ました。
これは、いずれの手法を用いたとしても、得られる近似曲線は同じであることを意味します。
では、各手法にはどのような相違点があるのでしょうか。

1つ目は、最尤法は観測データを確率変数と見なす確率モデルによる解法であるのに対し、最小二乗法は観測データを確定した値と見なす決定論モデルによる解法であるという点です。

実際、最尤法では、観測データを確率変数とみなし、観測データが得られるための尤もらしい値として、多項式の係数ベクトルを求めました。
一方、最小二乗法では、観測データは単なる数値であり、観測データと近似曲線の誤差が最小になるような値として、多項式の係数ベクトルを求めました。

このように、両者の間には観測データに対する思想の違いがあると言えます。

また、注意すべき点は、最小二乗法による解法は、最尤法と同様の以下の２つの事項を暗に仮定することです。

１）サンプリングノイズが平均０の正規分布に従うこと
２）各観測データが独立同分布に従うこと

つまり、**”両解法の目的関数が一致する”という事実は、”上記の仮定の下で最小二乗法を行うことの正当性は、確率モデルの観点からも支持できる”**と解釈することが可能です。

2つ目は、最尤法ではサンプリングノイズに関する知見を得ることが出来るのに対して、最小二乗法ではノイズに関する知見が得られないという点です。

最尤推定量として、ノイズの大きさを定量化できることは、最尤法を用いる大きなメリットと言えます。

4. まとめ

１）多項式フィッティング問題とは、観測データの背後に潜む関係性を、多項式により近似する問題である。
２）多項式フィッティング問題に対するアプローチとしては、最尤法と最小二乗法が知られている。
３）最小二乗法では、観測データを単なる数値と見なし、近似曲線との誤差が最小になるような値としてパラメタを決定する。
４）最尤法では、観測データを確率変数と見なし、手元のデータが生成される同時確率を最大するような値としてパラメタを決定する。
５）最尤法と最小二乗法のいずれの手法を用いても、最終的に二乗和誤差の最小化問題に帰着するため、得られる近似曲線は同一となるが、観測データのサンプリングノイズを定量化できる点で、最尤法の方が実用上優れた手法である。

5. 参考文献

[1] Christoper M. Bishop (2006) Pattern Recognition and Machine Learning
[2] 平井有三：はじめてのパターン認識
[3] http://palloc.hateblo.jp/entry/2016/01/17/231245
[4] http://enakai00.hatenablog.com/entry/2015/04/05/220817
[5] https://www.hellocybernetics.tech/entry/2016/04/24/055832
[6] https://www.hellocybernetics.tech/entry/2018/03/06/154317
[7] https://www.hellocybernetics.tech/entry/2018/03/06/051345

1. この状態を未学習(Underfitting)と呼ぶ。 ↩

2. この状態を過学習(Overfitting)と呼ぶ。 ↩

3. 最適化問題において、最大（最小）化を考える関数のことを指す。機械学習の問題は、ある制約条件下における目的関数の最適化問題に帰着することが出来る。 ↩

4. モデルが必要以上に複雑化することを防ぐために、目的関数に追加する項のことを指す。機械学習においては、L1正則化やL2正則化が広く用いられており、目的に応じて使い分けられる。 ↩

5. 平均値近傍にランダムノイズを伴い生成される確率変数の分布を表した連続型の確率分布である。ガウス分布とも呼ばれる。母数パラメタとして平均と分散を持ち、確率密度関数は左右対称の形状になる。指数型分布族(Exponential family)に属しており、密度関数が解析的に優れた性質を持つので、自然科学の実験における測定ノイズが従う分布として幅広く用いられている。 ↩

6. 観測データ点と近似曲線間の残差平方和を最小化するパラメタベクトル $\boldsymbol{w}$ を推定値として採用する手法である。 ↩

7. 連続型確率変数の実現値の相対度数を表す関数である。確率変数がある範囲の値をとる確率は、その範囲に渡り確率密度関数を積分すれことにより計算することができる。 ↩

8. 各確率変数が他の確率変数と同じ確率分布を持ち、かつ互いに独立していることを意味する。英語表記の頭文字を取り"i.i.d"と略記される場合も多い。 ↩