#はじめに
こんにちは。CDSLの@7vvXiです。
研究の一環としてBLEを使った屋内測位をしてみたので、そのメモになります。
筆者は全てESP-WROOM-32(ESP32)という機器を使ってやっています。
簡単なテストと実装方法について紹介したいと思います!
#BLE(Bluetooth Low Energy)とは
IT用語辞典より以下のような説明があります。
近距離無線通信技術Bluetoothの拡張仕様の一つで、極低電力で通信が可能なもの。
2010年7月に発表されたBluetooth 4.0規格の一部として策定された。
つまり、通常のBluetoothより消費電力を抑えた技術ということになります。
このBLEの電波の信号強度を使うことで、距離を推定し測位できるということです。
wifiよりも電波強度は弱くなるのでその点だけ注意です。
#三点測位とは
位置を測位する技術はフィンガープリント、AoA/AoD、カメラによる距離推定、機械学習...といった方法がありますが、その中の1つに三点測位があります。
まず、送信機を3つ受信機を1つ用意します(これは逆でも可能です)。
電波が球状に広がる性質を利用して2つの考え方ができます。
- 平面と仮定した「3つの円の交点」
- 立体と仮定した「3つの球の交線から交点座標を求める」
平面として考えた方が楽ですが、今回は後者の3次元的に考えてみます。
#座標の求め方
前提として、送信機の座標は全てわかっているものとして計算します。
また、受信機はスマホといった人が持っていることを想定して、
今回はz座標がわかっているとします。
この状態で受信機のx,y座標を求めていきます。
まず、各受信機を中心とする球の交線を考えていきます。
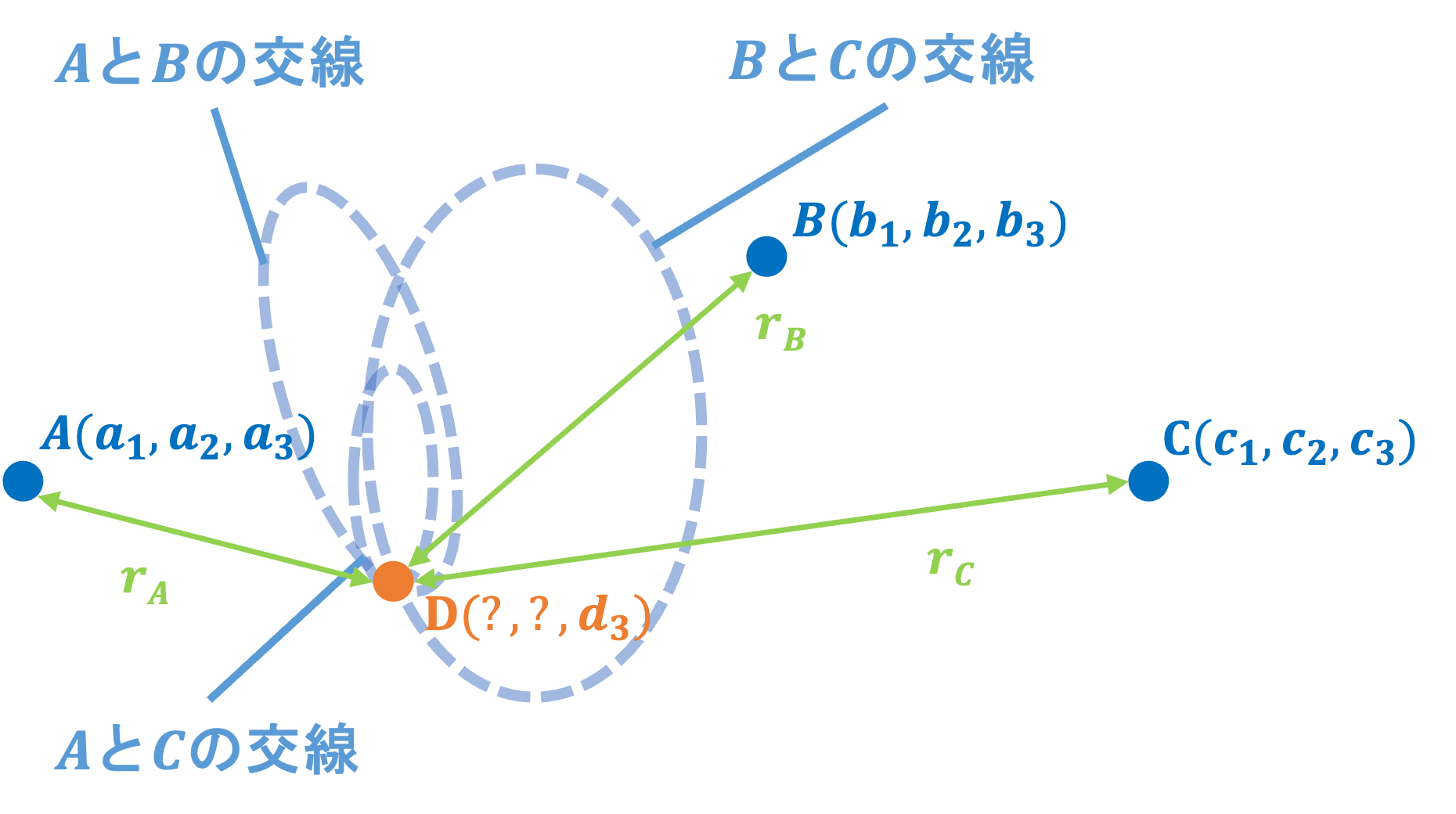
3つの送信機をそれぞれ$A, B, C$、受信機を$D$とすると、以下のような図として表せます。
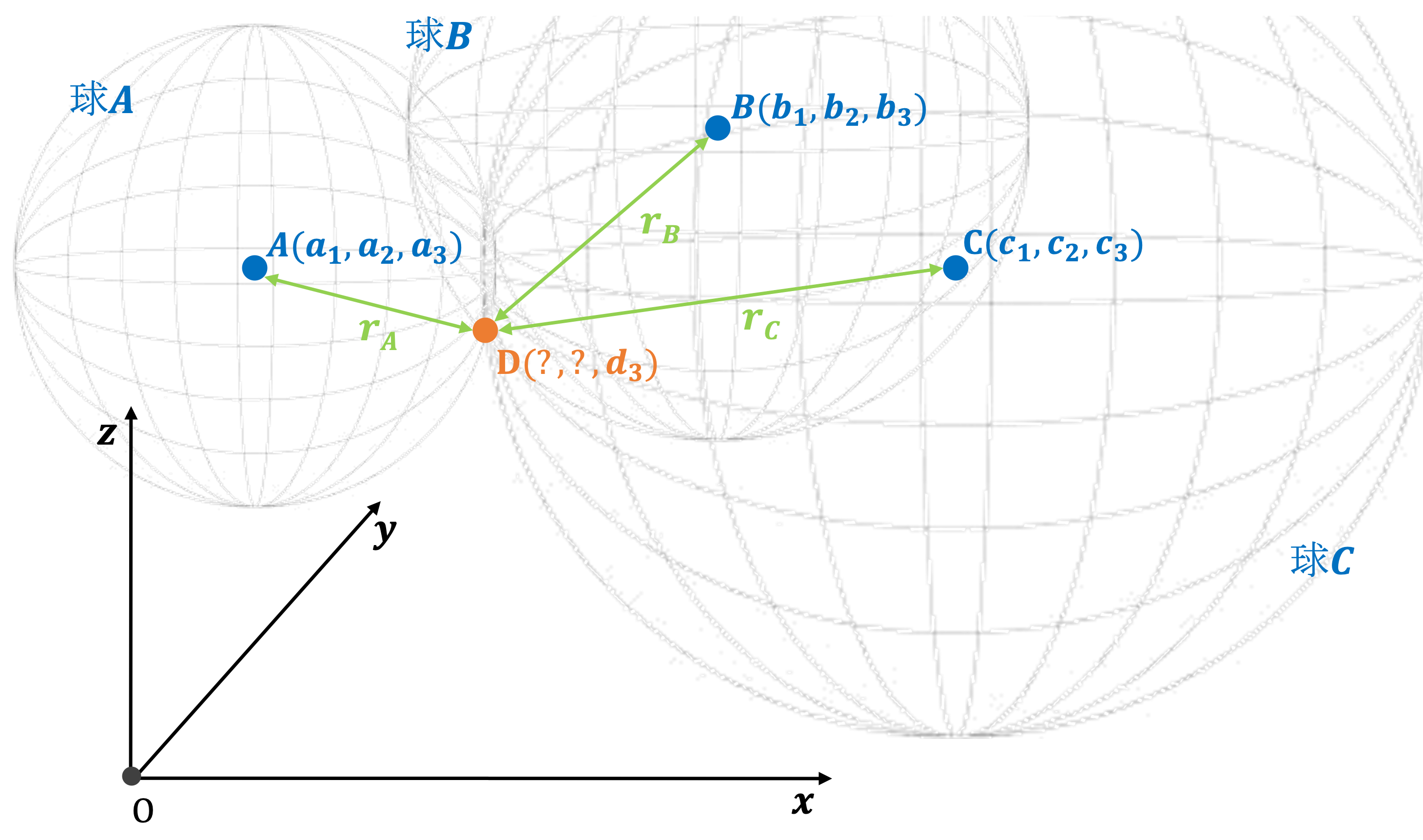
なお、各送信機の信号強度から距離に変換した値を$r_A, r_B, r_C$としています。
信号強度から距離に変換する方法はいくつか存在しますが、ここでは@shu223さんの記事を参考にしています。
受信機の位置が各送信機間のちょうど真ん中にいることはほとんどありえないため、球$A, B, C$の接触面は「交点」ではなく、「交線」になります。
数学的に整理すると、以下の式が成立することになります。
- $r_A + r_B > AB$
- $r_B + r_C > BC$
- $r_A + r_C > AC$
このように考えれば、3つの円の交点を求めるのと変わりません。
$A, B, C$を中心とする球面の方程式から2つ式を作ります。
- $(x-a_1)^2 + (y-a_2)^2 + (z-a_3)^2 = r_A^2$
- $(x-b_1)^2 + (y-b_2)^2 + (z-b_3)^2 = r_B^2$
- $(x-c_1)^2 + (y-c_2)^2 + (z-c_3)^2 = r_C^2$
つまり、2つの球面の交線(円)がのっている平面の方程式を求めています。
連立方程式として解くため、$A$と$B$・$B$と$C$・$A$と$C$どの組み合わせでもOKです。
例えば、$A, B$の組み合わせを整理すると以下のような式に表せます。
- $(2a_1-2b_1)x + (2a_2-2b_2)y + (2a_3-2b_3)z$
$= r_B^2 - r_A^2 + (a_1^2 + a_2^2 + a_3^2) - (b_1^2 + b_2^2 + b_3^2)$
ユーザが手に持っていると仮定して$z$の値を代入すると、2次方程式となります。
あとは、連立方程式を解くことで解が求まります。
#動作の検証
実際に動作するかをテストしてみました!
micropythonを用いたソースコード例を示しながら説明します。
まず、簡易的なテストのため、$z$座標は同一としています。
$A = (0, 0, 1), B = (0, 1, 1), C = (1, 1, 1), D = (?, ?, 1)$ とします。
$A, B, C$の座標から$D$の$x$座標と$y$座標を求めます。
なお、$r_A = r_B = r_C = \sqrt[2]{0.61}$です。
import math
#各座標の入力
A = (0, 0, 1)
B = (0, 1, 1)
C = (1, 1, 1)
R = (math.sqrt(0.61), math.sqrt(0.41), math.sqrt(0.41))
z = 1.0
#分解
a1, a2, a3 = A
b1, b2, b3 = B
c1, c2, c3 = C
ra, rb, rc = R
ちなみに正解は$D = (0.5, 0.6, 1)$です!
それでは、実際の計算部分について説明します。
まず、2つの球面の交線(円)が乗った平面の方程式を計算します。
#AとBから式を作る ー ①
def calc_AB():
ABx = 2 * a1 - 2 * b1
ABy = 2 * a2 - 2 * b2
ABr = (rb ** 2 - ra ** 2) + (a1 ** 2 + a2 ** 2 + a3 ** 2) - (b1 ** 2 + b2 ** 2 + b3 ** 2) - ((2 * a3 - 2 * b3) * z)
return ABx, ABy, ABr
#AとCから式を作る ー ②
def calc_AC():
ACx = 2 * a1 - 2 * c1
ACy = 2 * a2 - 2 * c2
ACr = (rc ** 2 - ra ** 2) + (a1 ** 2 + a2 ** 2 + a3 ** 2) - (c1 ** 2 + c2 ** 2 + c3 ** 2) - ((2 * a3 - 2 * c3) * z)
return ACx, ACy, ACr
#BとCから式を作る ー ③
def calc_BC():
BCx = 2 * b1 - 2 * c1
BCy = 2 * b2 - 2 * c2
BCr = (rc ** 2 - rb ** 2) + (b1 ** 2 + b2 ** 2 + b3 ** 2) - (c1 ** 2 + c2 ** 2 + c3 ** 2) - ((2 * b3 - 2 * c3) * z)
return BCx, BCy, BCr
$x, y$の係数と右辺の定数部分をそれぞれ変数に格納しています。
そして、$x, y$を求めてみます!
#① - ② (yを削除)
ABx *= ACy
ABr *= ACy
ACx *= ABy
ACr *= ABy
#xを求める
x = ABx - ACx
r = ABr - ACr
x = r / x
#yを求める
ABx, ABy, ABr = calc_AB()
ABx *= x
ABr -= ABx
y = ABr / ABy
print(x, y) #0.5000000000000001 0.6
出力結果は0.5000000000000001 0.6となりました。
ほとんど誤差なく計算できていますね!
#終わりに
今回は3次元での三点測位方法について紹介しました。
3次元で計算を行うことで、2次元よりも精度が期待できます!
しかし、電波が球状に広がるのはあくまで理論値です。
2.4GHz帯の電波はWifiや他の電波から干渉を受けやすく、誤差が出やすいです。
いかにして信号強度から距離に変換するかが鍵となっていると思います。
何かアドバイスや疑問点がありましたら、コメントお願いいたします!