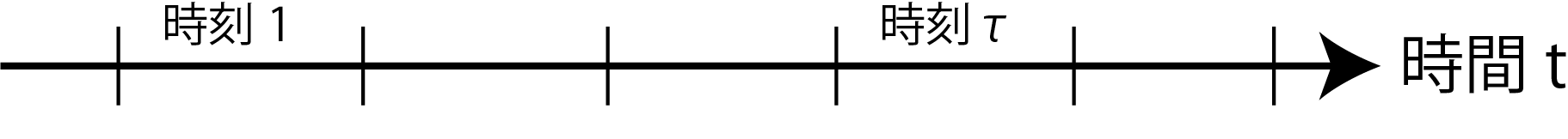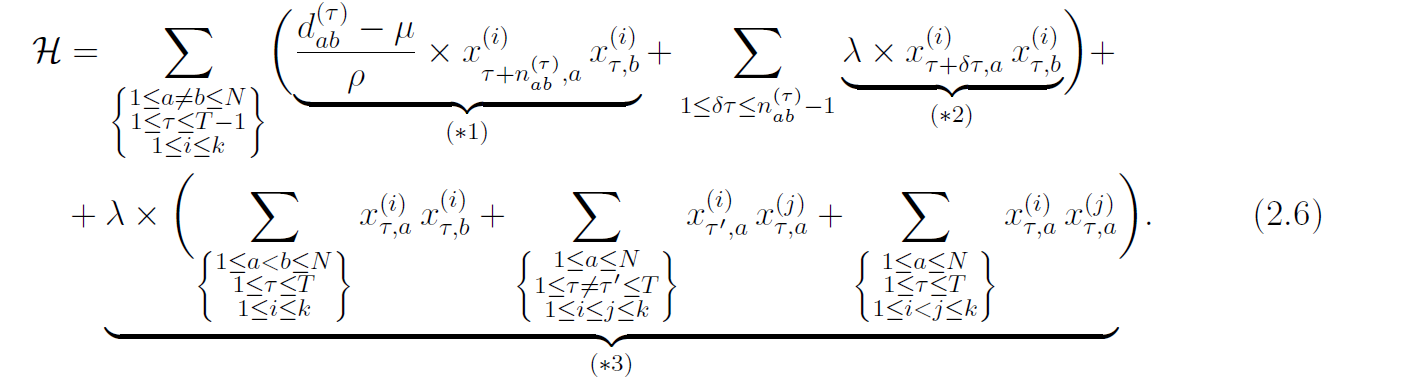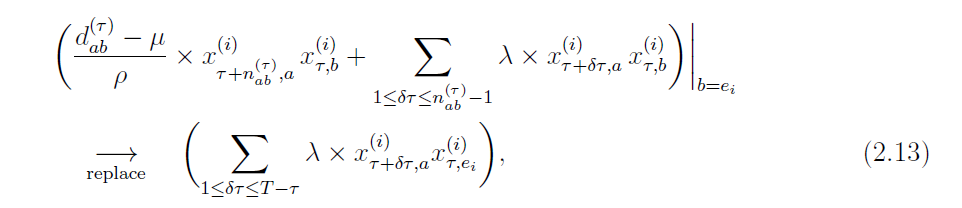Jij, QunaSysでインターンを行っているヒデトです。
デンソーの論文"Quantum Annealing of Vehicle Routing Problem with Time, State and Capacity"を読んだので、まとめます。
読んだ論文
[1] Quantum Annealing of Vehicle Routing Problem with Time, State and Cappacity
https://arxiv.org/abs/1903.06322
概要
この論文では、巡回セールスマン問題(TSP)の一般化した問題である、配送計画問題(VRP)をQUBOの形式に定式化しています。
どのように定式化を行っているかというと、VRPを実務で使えるよう、様々な制約や条件を組み込めるようしています。
今回の提案されて定式化で扱えるようになるものは
・配送におけるスケジュール(時間)
・様々な容量(トラックの荷物の容量など)
・配送先での作業時間(荷物を降ろしたりする時間)
などなど様々な状況を式で再現できるようになります。
VRPについては1回Qiitaにまとめたのでそっちを参照してください。
容量制約有りの配送計画問題(CVRP)を量子アニーリングで解く
巡回セールスマン問題の確認
VRPの特殊ケースにあたるTSPを従来の定式化を踏まえて確認します。
まず巡回セールスマン問題とは、複数の都市と都市間を移動するときのコストが与えられた際に
「全ての都市を回るpathの中で、最もコストの低いpathはどれか」
を探す問題です。
定式化にあたり以下の0-1変数を使います。
$x_{ia}$ : 都市$a$を$i$番目に訪問するとき$1$, そうでないとき0
また、都市$a$と都市$b$の移動の際のコストを$d_{ab}$とかけば目的関数にあたるハミルトニアン$H_{cost}$は以下のようになります。
H_{cost} = \sum_{i,a,b} d_{ab} x_{i,a} x_{i+1, b}
次に制約条件を考えます。
今回の制約は以下の2つが必要になります。
-
同時に2つの都市は訪問できない
$$
\sum_{a} x_{i,a} = 1 \ \ \ \ \ \forall i
$$ -
全ての都市はちょうど1回限り訪問する
$$
\sum_{i} x_{i,a} = 1 \ \ \ \ \ \forall a
$$
上記の制約を破った際にコストが上昇するように二乗の形に変形し、制約条件に対応するハミルトニアン$H_{st}$を次のようにします。
$$
H_{st} = \sum_{i}(\sum_{a} x_{i,a} - 1)^2 + \sum_{a} (\sum_{i} x_{i,a} - 1)^2
$$
以上よりTSPのハミルトニアンは以下のようにすれば良さそうです。
$$
H = H_{cost} + H_{st} = A * \sum_{i,a,b} d_{ab} x_{i,a} x_{i+1, b} + B * { \sum_{i}(\sum_{a} x_{i,a} - 1)^2 + \sum_{a} (\sum_{i} x_{i,a} - 1)^2 }
$$
この定式化をVRPに拡張しただけでは、扱える情報は都市を訪れる"順番"だけであり、時間は疎かトラックの容量なども扱えなさそうです。
時間を考慮したVRP
では、時間を考慮したVRPの定式化を行います。
時間は通常連続的な変数ですが、今回はQUBOとして定式化したいので時間を分割して時刻として考えます。
時間$t_{\tau}$から時間$t_{\tau +1}$を時刻$\tau$とします。すなわち、
$$
\tau \mapsto [t_{\tau}, t_{\tau + 1} ) \ \ \ \ \ (1 \leq \tau \leq T -1 ), \ \ \ \ \ \ \ t_{\tau + 1} - t_{\tau} \equiv \Delta t.
$$
以上時刻の概念を踏まえて、今回用いる変数が以下です。
$x_{\tau , a} ^{(i)}$ : トラック$i$が都市$a$を時刻$\tau$に訪問するとき1、そうでないとき0であるバイナリ変数.
そして今回は、都市$b$から都市$a$へ移動する際の所要時間とコストが与えられるものとします。
所要時間に関しては、時刻に関するように変形します。すなわち所要時間は、時刻何個分かで表します。
$$
n_{ab}^{(\tau)} = \lceil \frac{時刻\tau において、都市aからbへ移動する際の所要時間}{\Delta t}\rceil
$$
($\lceil \rceil$は天井関数。e.g. $\lceil 2.7 \rceil = 3$)
また移動の際にかかるコストは以下のようにします。
$d_{ab}^{(\tau )} $ : 時刻$\tau$において、都市bからaへ移動する際にかかるコスト(所与).
トラックの総数を$i$、都市の総数を$N$、考えたい時間枠を$[t_1 , t_T]$とします。そうすると、目的関数と制約式を含めた問題ハミルトニアンは以下のようになります。
(* 1) : 目的関数. 全ての経路におけるコストの総和. 係数が$(d_{ab}^{(\tau)} - \mu) / \rho$になっているのは後述.
(* 2) : 時刻の概念を導入したことにより出てきた制約式. 都市$b$ → $a$ へ $n_{ab}^{(\tau)}$より少ない時刻で到着することを禁止する項. そのため$n_{ab}^{(\tau)}$より小さい$\delta \tau$について、$x_{\tau + \delta \tau , a}^{(i)} x_{\tau , b}^{(i)}$の総和をとっている.
(* 3) : VRP(or TSP)に存在する典型的な制約式.
第一項 : 同じトラックが、同じ時刻に異なる都市を訪問することを禁止する項.
第二項 : 全ての都市を複数回訪れることを禁止する項.
第三項 : 異なるトラックが、同じ時刻に同じ都市を訪問することを禁止する項.
実際にはこれに加えて、「巡回セールスマン問題の確認」のところの制約等を入れたほうが良さそうです。
目的関数、制約条件の係数について
ハミルトニアンにおけるパラメータ$$(\rho , \mu , \lambda )$$をどのようにするかを説明します。
まず答えから言うと、パラメータは基本的に以下のように設定します。
$$
\mu = d_{max} , \ \ \ \ \rho = \frac{d_{max} - d_{min}}{\lambda}
$$
$\mu = d_{max}$と目的関数の係数が$(d_{ab}^{(\tau)} - \mu)/ \rho$になっているからわかる通り、目的関数の係数が全て負の値を取るようにシフトします。
ではその説明です。
今回の問題ハミルトニアンを単純化すると以下のようにかくことができます。
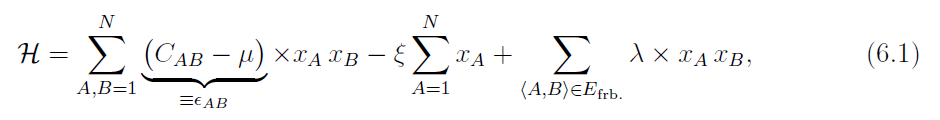
第一項が目的関数にあたり、$C_{AB} > 0$です。そして第三項が制約式にあたり、$E_{frb}$は制約式を満たさない解の集合です。第二項は一次の項です。
従来のパラメータの選び方としては、TSPでは $\xi = \lambda$, VRPでは $\xi \geq \frac{3}{2} \lambda$ とし、$\mu = 0$としています。つまり、負の方向へのシフトは行っていません。
ここで$\xi = 0 , \lambda > 0$であったときを考えてみます。このときの基底状態は$x_{A} = 0 (for \forall A)$となります。
つまり、$\xi-$項は基底状態のqubitを$0 → 1$へと変化させる項だと考えることができるわけです。
このような$\xi-$項の効果は、$\xi$の項を使わなくても作ることができます。
それはすなわち、$\mu$ を使って目的関数の項を全て負の方向にシフトすることで達成されます。
そうすることによって、$\xi-$項を無くしたり、他のことのために使ったりすることができます。
そのためまずは、$\mu$を$\epsilon_{AB}$が全て負の値になるように設定します
$$
\epsilon_{AB} = C_{AB} - \mu < 0,\ \ \ \ \ for \ \ \ \forall (A,B)
$$
次に$\lambda$についてです。$\lambda$は次のように設定します。
$$
\epsilon_{AB} + \lambda > 0 , \ \ \ \ \ for \ \ \ \forall (A,B)
$$
こうすることによって、$H = 0$を実行可能解かどうかのベースラインとして引くことができます。
以上より$\epsilon$の範囲は以下をパラメータの基本値として設定します。
$$
-\lambda = \epsilon_{min} \leq \epsilon_{AB} \leq \epsilon_{max} = 0
$$
これを$(\rho , \mu , \lambda )$の関係式にすると
$$
\mu = d_{max} , \ \ \ \ \rho = \frac{d_{max} - d_{min}}{\lambda}
$$
となります。
その他の条件「始点と終点が決まっている」
今回モデル化した式で、その他の条件を埋め込むときのことを考えます。
実務を考えたときに、存在しうる条件は以下があると思います。
(i) : それぞれのトラックの出発地点が決まっている.
(ii) : それぞれのトラックの終着地点が決まっている.
(i) : 出発地点について
トラック$i$の出発地点が$s_{i}$のときは、最初の時刻$\tau = 1$における地点を指定してあげればよいのです。記述にはデルタ関数を使っています。
$$
x_{1, a}^{(i)} = \delta_{a, s_{i}}
$$
(ii) : 終着地点について
出発地点とは違い、終着地点はどの時刻に到着するか基本的にわからないためもう少し工夫が必要です。
まずは、トラック$i$の終着地点$e_{i}$の1つ前に訪問する場所$a$に着目します。
サービス終了時刻$T$以内では$e_{i}$に行けないような、前の地点$a$と時刻$\tau$の組み合わせを消します。
すなわち
$$
x_{\tau , a}^{(i)} = 0 \ \ \ \ for \ \ \ \ \ \tau + n_{e_{i} , a}^{(\tau)} >T
$$
これに加えて、$e_{i}$に着いた後に他にどこかの都市に行くことを禁止しなくてはいけません。
以上を踏まえると、(2.6)式一項二項の$b = e_{i}$に関する式は次のように書き換えることができます。
$e_{i}$の次にはどこにも行けないので、$x_{\tau + n_{ae_{i}}, a}^{(i)} = 0$です。よって、第一項は消すことができます。
複数の容量を加えたVRP
トラックに積む荷物の重さや、大きさなど様々な容量に関する状態を記述したいときのことについて考えます。
ちなみに今回みたいに、時間を区切って時刻として考えれば"時間"も一種の容量だと考えることもできます。
ですので、容量制約に関しての定式化は時刻の場面と似ています。
使う変数は、これまでの変数に$M$個の容量を表す添字を挿入します。
$$
x_{\tau , a | c_1 ,c_2 , \ldots , c_M}^{(i)}
$$
容量の下限と上限は以下のようにします。
$$
q_m \leq c_m \leq Q_m \ \ \ (q_m , Q_m \in Z, 1 \leq m \leq M).
$$
また簡単のため、$c = (c_1 , c_2 , \ldots , c_M)$とかきます。
$$
x_{\tau , a | c}^{(i)} : トラックi のM個の容量の状況がc のときかつ、時刻\tau に都市a を訪問するとき1、そうでないとき0
$$
都市間の移動で$m$番目の容量の変化を$B_{ab | m}^{(\tau)}$とします。
$$
B_{ab | m}^{(\tau)} = 時刻\tau において都市aからbへ移動する際のc_mの変化
$$
同様に$B_{ab}^{(\tau)} \equiv (B_{ab|1}^{(\tau)} , B_{ab | 2}^{(\tau)}, \ldots , B_{ab | M}^{(\tau)})$とかきます。
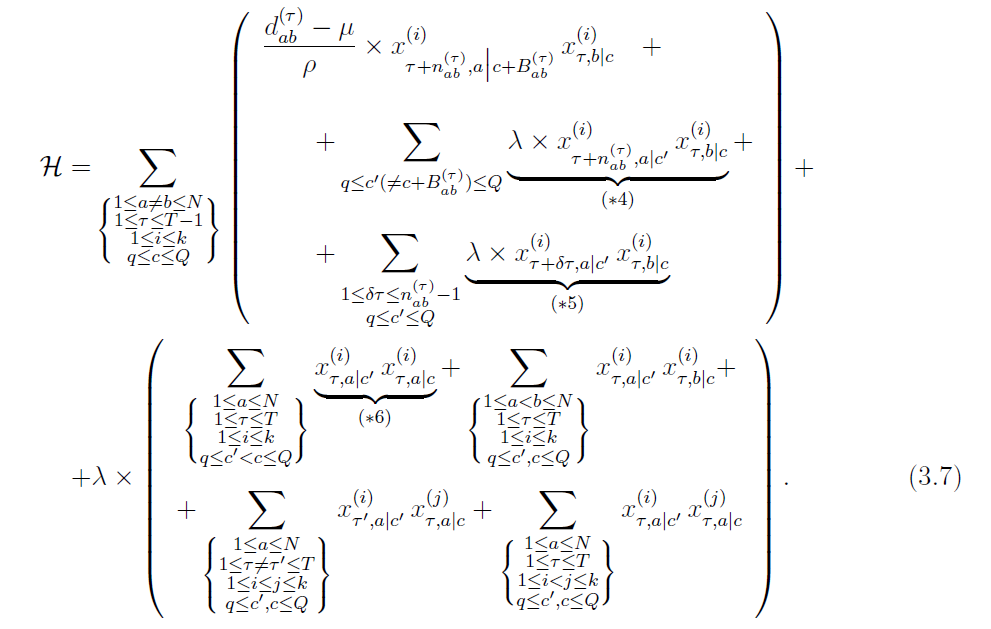
これらを用いれば複数の容量を用いたVRPは以下のようにかくことができます。
(* 4) : 適正でない容量の変化を禁止する項.
(* 5) : どんな容量の変化においても、都市$b$ → $a$ へ $n_{ab}^{(\tau)}$より短い時間で到着することを禁止する項.
(* 6) : $i , \tau , a$が同じとき、複数の$c$に1の割当を禁止する項.
その他の項は、式(2.6)での制約と同じです。
訪問先での作業時間を考慮したVRP
訪問した場所で、荷物を降ろしたり積んだりする作業時間は無視できないほど存在します。
これらの作業時間を組み込んだVRPの定式化について説明します。
ここでは今まで使っていた変数$x$を、到着と出発に分離します。すなわち以下のような変数を使用します。
$$
\hat{x}_{\tau, a}^{(i)} : トラックiが, 時刻\tau に都市a に到着したとき1、そうでないとき0
$$
$$
x_{\tau , a}^{(i)} : トラックiが, 時刻\tau に都市a を出発するとき1,そうでないとき0
$$
このように変数を設定すると、都市間の移動時間と、ある都市での作業時間を分けて考えることができます。
(1)都市間の移動:$ x \rightarrow \hat{x}$
(2)都市での作業:$ \hat{x} \rightarrow x$
これに加えて都市$a$での作業時間$n_{a}^{(\tau)}$を導入しましょう。
$$
n_a^{(\tau)} = \lceil \frac{時刻\tau における都市aでの作業時間}{\Delta t} \rceil \geq 1
$$
これらを使えば、式(2.6)に作業時間を加えたハミルトニアンは次のようにかくことができます。
最初の( ) が (1)移動 に関する目的関数及び制約です。
新たに加わった制約として、$ x \rightarrow x$(移動→移動)を禁止する項が三項目に導入されています。
2つめの( ) が (2)作業 に関する目的関数及び制約です。
同様に、$\hat{x} \rightarrow \hat{x}$(作業→作業)を禁止する項が三項目に導入されています。
3つめの( ) はこれまで同様の制約(複数回訪問してはいけないなど)を今回の変数で記述したものです。
その他の条件
今回行ったモデル化で、扱うことの出来る他の条件を説明します。
論文では定式化は行っていませんが、過去のVRPに関する論文を読んだりしたりすれば定式化できると思います。
-
配送の優先サービス
顧客の中には、優先的にサービスを受けられる権利を購入している人々がいることが考えられる。
こういった場合には、それらの顧客のコストを他より小さくすることで同様のモデル化できる。 -
時間枠制約
宅配には、通常配送時間を指定するサービスが存在する。
このような制約は、配達できない時刻にその顧客を訪問するようなqubitを0とすることで達成できる。(i.e. $x_{\tau , a, | c}^{(i)} = 0 $ ) -
車種指定制約
荷物の大きさなど、サービスを提供する車種を指定する状況が発生しうる。
このような場合も2と同様に、qubitを0とすることによって、達成できる。 -
容量制約
複数の容量制約を加えたVRPを用いて、不可能なqubitを消すことで達成できる。 -
配達員の休憩時間
作業時間を加えたVRPを用いて、休憩時間をすることができる。
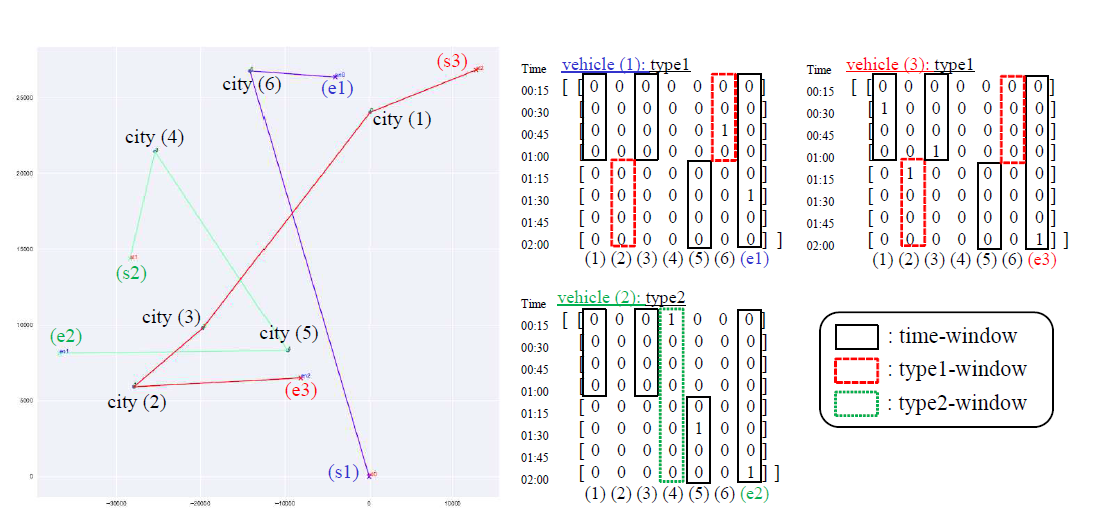
実験
実際にD-Wave 2000Qを使って数値実験をしたようです。
顧客数6, トラック数3, 時間枠2時間, 時間の分割を15分ごと で数値実験を行っています。
その結果が以下の図です。
10,000回計算を行って、最適解が求まっているようです。定式化の有効性がわかります。
ただ問題サイズが非常に小さいので、この結果が良いのか悪いのかはわかりません。
10,00回の計算の中で、80%が実行可能解だったそうです。
考察
今回の定式化は、
「様々な連続的な変数をいくつかに区切って、0-1変数$x_{ab}$の添字に挿入している」
ということができます。
そのため、理論的には実社会に存在する条件をモデル化することに成功しています。
しかしその一方で、添字に様々な連続変数を挿入しているため用いるqubit数が膨大な数になってしまっています。
なので現段階のD-waveで実装しようと思ったら、都市数は非常に限られた10以下程度になると思います。
この論文を読んでひとつ思ったのが、
QUBOの定式化は、通常の定式化を行う際のテクニックなどの多くが使われているという所です。
例えば、今回の作業時間を考慮した際の定式化などは、僕もどこかのVRPの論文で同じようなことをしているのを見たことがあります。
ですので、通常の最適化の論文を読むのは非常に重要だとわかります。