QunaSysでインターンを行っているヒデトです。
今日はまたまたVolkswagenが発表したQAOA(Quantum Approximate Optimization Algorithm)とQA(Quantum Annealing, 量子アニーリング),SA(Simulated Annealing シミュレーティッドアニーリング, 焼きなまし法)を比較した論文を読んだのでそれをまとめたいと思います。
よろしければQAOAについては以下の記事をご覧になってください。
https://qiita.com/snhrhdt/items/ae55a94b25c06142528a
*前回のQAOAの記事と使っている記号が異なっていたり、最大化が最小化になっていたりしますが、それは今回読んだ論文に合わせています。
読んだ論文
[1] Comparison of QAOA with Quantum and Simulated Annealing
https://arxiv.org/abs/1901.01903
Volkswagenグループの人たちがまとめた論文になります。Volkswagenは量子コンピュータにとても力を入れているんですね。
余談ですが、僕が今までまとめた論文は3/4がVolkswagenグループのものですね。
[2] Seeking Quantum Speedup Through Spin Glasses: The Good, the Bad, and the Ugly
https://arxiv.org/abs/1505.01545
こちらの論文は読んではいないのですが、今回の記事で引用させていただいているので挙げておきます。
概要
現在量子情報技術を利用したアルゴリズムの中に、QAOAやQA(量子アニーリング)が存在します。
また一方で古典的なアルゴリズムには、熱的な振動を模したSA(焼きなまし法)というアルゴリズムも存在します。
これらのアルゴリズムの"違い"をこの論文では考えています。
この論文では
まず、QAOAが1回の反復で必ず解ける問題(問題のハミルトニアンかつQAOAのパラメーターの条件)を考えます。
そのような問題の集合を考えると、その集合の中にQAやSAが扱いづらい問題の集合が含まれていることを確認します。
要するにQAOAでは解けるが、QAやSAでは解ける確率が低い問題の存在を確認することによって比較を行います。
QAOAの概略
QAOAはゲート式の量子コンピュータ上で動作する、組み合わせ最適化に対するアルゴリズムです。
現在の、ビット数も少なく誤り訂正もままならない量子コンピュータ(Noisy Intermediate-Scale Quantum:NISQデバイス) に対する有望なアルゴリズムだと期待されています。
QAOAでは、基底状態を求めたいハミルトニアン$H_P$とは別に、自明な基底状態を持つハミルトニアン$H_X = \sum \sigma^{(i)}_X$を用います。
$H_X$の基底状態である、計算基底の全ての重ね合わせ$|+ \rangle $に、$\exp(-i \beta _ {p} {H} _X ) \exp(-i \gamma _{p} {H} _P ) $を繰り返し$p$回作用させます。
作用させた状態を
$$
|\Phi(\gamma , \beta) \rangle = \exp(-i \beta _ {p} H _ {X}) \exp(-i \gamma _ {p} H _P) ...\exp(-i \beta _1 H _{X}) \exp(-i \gamma _{1} H _P)|+ \rangle
$$
とします。
この時の状態で$H_P$を測定した時の期待値が最小になるようにパラメータ$\gamma , \beta$の値をグリッドサーチなどによって探索します。
$ p → \infty$とすることはQAA(量子断熱計算)で時間変化を無限小にすることに対応しており、基底状態を得ることができます。
今回はこの反復回数$p$を1回にして考えます。
決定的QAOA
今回は1回の反復($p=1$)での決定的QAOA(必ず最適解を出力してくれるQAOA)の条件を考えます。
求める問題ハミルトニアンを$H_P=diag(E_1 , E_2 , \ldots ,E_{2^N}$)とし、$H_P$の求めたい基底状態を$|t \rangle$としましょう。
この時に必ず最適解を出力されるということは、$|t \rangle $を得られる確率が1だということです。
すなわち、
$$
\big| \langle t \ | \ \gamma, \beta \rangle \big| ^2 \ = \ 1 .
$$
では、この式を展開して$\gamma , \beta , H_P$にどのような条件があるのか確かめます。
その前に、式展開中で使う文字を先に説明しておきます。
$|l \rangle $ : $|+\rangle$を展開した$l$番目の状態。すなわち、$|l \rangle = |0...0 \rangle 〜 \ |1...1\rangle$。
$\Delta_t(l)$ : $|t \rangle $と$|l \rangle $のハミング距離(ハミング距離とは、2つのビット列において異なるビットの個数)。
$E_l$ : $|l\rangle$の$H_P$に関する固有エネルギー。すなわち、$H_P |l\rangle = E_l |l \rangle$ 。
$$
\langle \ t \ | \ \gamma , \beta \rangle = \langle \ t \ | \ e^{-i \beta H_X} \ e^{-i \gamma H_P} \ | + \rangle \
$$
まずこの式に、$|+ \rangle = \frac{1}{\sqrt{2^N}} \sum^{2^N} _l |l \rangle$を代入し、$H_P |l \rangle = E _l |l \rangle$を使うと下記のようになります。
$$
= \frac{1}{\sqrt{2^N}} \sum^{2^N} _{l} e^{-i \gamma E _l} \langle t | e^{-i \beta H _X} |l \rangle
$$
そして$e^{-i \beta H_X}$を展開します。
$$
= \frac{1}{\sqrt{2^N}} \sum^{2^N}_{l} e^{-i \gamma E_l} \langle t | \ \prod^N _{j=1} \{ \cos(\beta) - i \sin(\beta) \sigma^{(j)} _X \} \ |l \rangle
$$
さらに$\sigma^{(j)}_X$は$j$番目のqubitを反転させる演算子であるので、以下が成り立ちます。
$$
\text{$\langle t | \sigma^{(j)}_X |l \rangle \ =$}
\begin{cases}
\text{1 $\ $( $j$番目のスピン方向のみが異なるとき)} \
\text{0 $\ $(その他)}
\end{cases}
$$
$e^{-i\beta H_X}$の中身をさらに展開してみます。
$$
\prod^N _{i=1} \{ \cos(\beta) - i \sin(\beta) \sigma^{(i)} _X \} = (\cos(\beta))^N + (\cos(\beta))^{N-1} ( -i\sin(\beta) ) \sum^N _{i=1} \sigma^{(i)} _X + \dots + (-i \sin(\beta) )^N \prod^N _{i=1} \sigma^{(i)} _X
$$
上記右辺の第一項は$\sigma_X$がかかってないので$|t \rangle $と全く同じ状態に作用するとき、すなわち$\Delta _t (l) =0$となる$| l \rangle $に関してのみ$\langle t | (\cos(\beta) )^N |l \rangle = 1$となります。第二項は$\Delta _t(l) =1$となる$|l \rangle$に作用するときに1となります。以下同様です。
$\Delta _t(l) = n$となる状態の個数は${}_N C_n$個存在することを踏まえて、$l$に関する総和で表せば
$$
\langle \ t \ | \ \gamma , \beta \rangle = \langle \ t \ | \ e^{-i \beta H_X} \ e^{-i \gamma H_P} \ | + \rangle \
$$
$$
= \frac{1}{\sqrt{2^N}} \sum^{2^N}_{l=1} \exp \bigl(-i(\gamma E _l + \frac{\pi}{2} \Delta _ t(l)) \bigr) \cos (\beta)^{N-\Delta _t (l)} \sin (\beta)^{\Delta _t (l)} \ \ \ \ \dots (1)式
$$
となります( $-i = e^{-i \frac{\pi}{2}}$ としてまとめています)。
① $\beta$に関する条件
(1)式の$\sum$を全て展開すると$2^N$個の複素数の和になります。$\sum$を展開した各項の絶対値の最大は$\frac{1}{\sqrt{2^N}}$であり、これは$\beta = \pi /4 $のときに達成されます。
よって、(1)が1になるときの$\beta$の条件は$\beta = \pi /4$となります。
② $\gamma$と$H_P(各 E_l)$に関する条件
$\gamma , E_l$がexpの肩にかかっていることからわかるように、expの波の位相がずれていてはそれぞれが打ち消し合ってしまいます。
つまり①の$\beta$に関する条件だけでは(1)式の総和が1未満になってしまいます。
ですのでexpの位相が全て揃っている条件が必要です。それは以下の$\gamma$と$H_P$に関する以下の条件が成り立つことです。
$$
(\gamma E_l + \frac{\pi}{2} \Delta_t(l) ) \mod 2\pi = c \ \ \ \forall l = \{1,2,...2^{N} \} \dots (2)式
$$
以上の①と②が決定的QAOAに対する条件になります。
「全ての位相が揃う」ということからわかると思いますが、このような問題のクラスはとても狭い範囲のものです。
対応するスピングラス系
p=1の決定的QAOAの問題の中で、QAとSAが扱いづらい問題を見つけます。
その為に、ここでは上記の条件をスピングラス系に対応させます。
注意して欲しいのが、上での条件とこれから作るハミルトニアンは同値ではないということです。
スピングラスのハミルトニアンの中で、上記の条件を満たすものを作ります。
スピングラス系は次のようなハミルトニアンを持っています。
$$
H= \sum_{i_1}^N h_{i_1} \sigma_z^{(i_1)} + \sum_{i_1 , i_2}^N J_{i_1,i_2} \sigma_z^{(i_1)} \sigma_z^{(i_2)} + \sum_{i_1 , i_2 , i_3}^N J_{i_1,i_2,i_3} \sigma_z^{(i_1)} \sigma_z^{(i_2)} \sigma_z^{(i_3)} + ....
$$
$\sigma_z^{i}$はそれぞれのスピンの方向に対応しており、$h_{i}$は縦磁場であり、$J$はそれぞれ相互作用を表しています。
スピングラス系のハミルトニアンを変形する為に、以下の関係式を使います。ここで$t_i$は、$|t \rangle $の$i$番目のqubitです。
$$
\sum^N _{i} t _i \sigma^{(i)} _z = N - 2 \tilde{\Delta} _t
$$
$\tilde{\Delta} _t$はハミング距離演算子であり、固有値がハミング距離で固有状態がそれぞれの計算基底になります(すなわち、$\tilde{\Delta} _t |l \rangle = \Delta _t(l) |l \rangle$ )。
この式はスピン系の総磁荷で考えるとわかりやすいです。例えば$|t \rangle $が全て上向きのスピンだったとき、右辺の値は1つのスピンが異なるごとに総磁荷が2下がります。
このとき同様に左辺も、+1だった項が1つ減り、-1の項が1つ増えるので2下がります。
論文では上記の式をそのまま使っているのですが、このままだと$|t \rangle $と全てのスピン方向が異なる時が基底状態となってしまうので、(-1)倍した方が良さそうです。
以上の関係式を用いてスピングラスハミルトニアンの中で以下のようなものを構成します。ここで、$H_{2\pi}$は全ての固有値が$2\pi$の倍数である任意のスピングラスハミルトニアンで、エネルギーを定数倍することで容易に作ることができます。
$$
H _{SG} = \frac{\pi}{4} \sum^N _i (- t _i) \sigma^{(i)} _z + H _{2\pi} \dots (3)式
$$
このときスピングラスハミルトニアンを上記のように構成すると、確かに(2)式の位相が揃う条件を満たすことを確認します。
$\gamma = -1$とし、$|l \rangle$に対する$H_{2\pi}$の固有値を$2 \pi c'(l)$ ($c'(l)$は整数)とすれば、
$$
(2)式 = -i\bigl( \frac{\pi}{4} (N - 2\Delta_t(l) ) - 2 \pi c'(l) + \frac{\pi}{2} \Delta _t(l) \bigr)
$$
$$
= -i\bigr( \frac{\pi}{4} N - 2 \pi c'(l) \bigl)
$$
となり、確かに(1)式$\langle \ t \ | \ \gamma , \beta \rangle = 1$となることがわかります。
QAとSAについて
上記で議論した$p=1$の決定的QAOAが解ける問題クラスのうち、QAとSAが解きにくいような問題を探します。
その為に、まずはQAとSAの性質について考えてみましょう。
QAはD-WAVEのあの量子アニーリングのことで、SAは古典コンピュータでよく使われるアルゴリズムです。
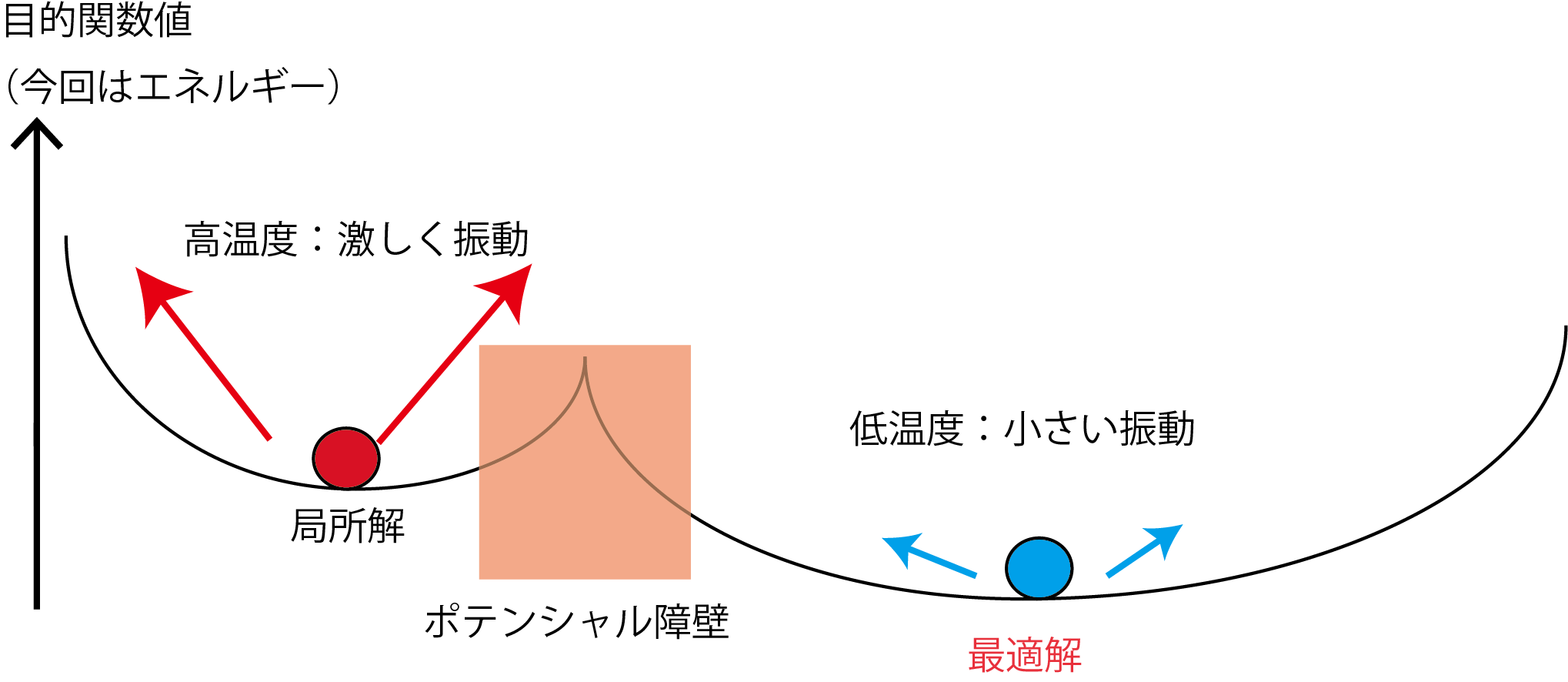
SA(Simulated Annealing)
SAは、熱的な振動を模したアルゴリズムになります。
通常のアルゴリズムというのは、常に目的関数値が下がる方向に探索を続けます。常に坂道を降るような感覚です。
しかしこれでは、局所解に陥ってしまいます。
そこでSAではアルゴリズム内に温度に対応するパラメーターを用意し、
温度が高い時には高い確率で、目的関数値が減少する方向とは逆の方向に向かいます。
温度が高い時には、原子が激しく振動しているイメージです。
探索を続けるうちに、温度のパラメータを徐々に下げ、温度が0となれば探索終了です。
このアルゴリズムが苦手とする問題は、ポテンシャル障壁が高い場合です。
すなわち、ポテンシャル障壁が高いと目的関数値が増加する方向に進んでも進んでもそのポテンシャル障壁を超えられないということです。
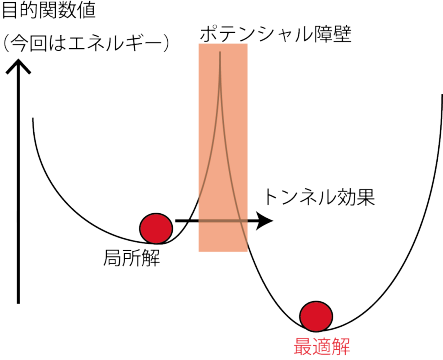
QA(Quantum Annealing)
QAはSAに加えて、トンネル効果が現れると言われています。
最適解が高いポテンシャル障壁で遮られている場合でも、ポテンシャル障壁を超えるのではなく、トンネル効果で通り抜けることによって、最適解にたどり着こうとします。
QAが苦手な問題はというと、ポテンシャル障壁が厚い場合です。
トンネル効果が現れる確率は、ポテンシャル障壁の壁に対して指数的に減少します。
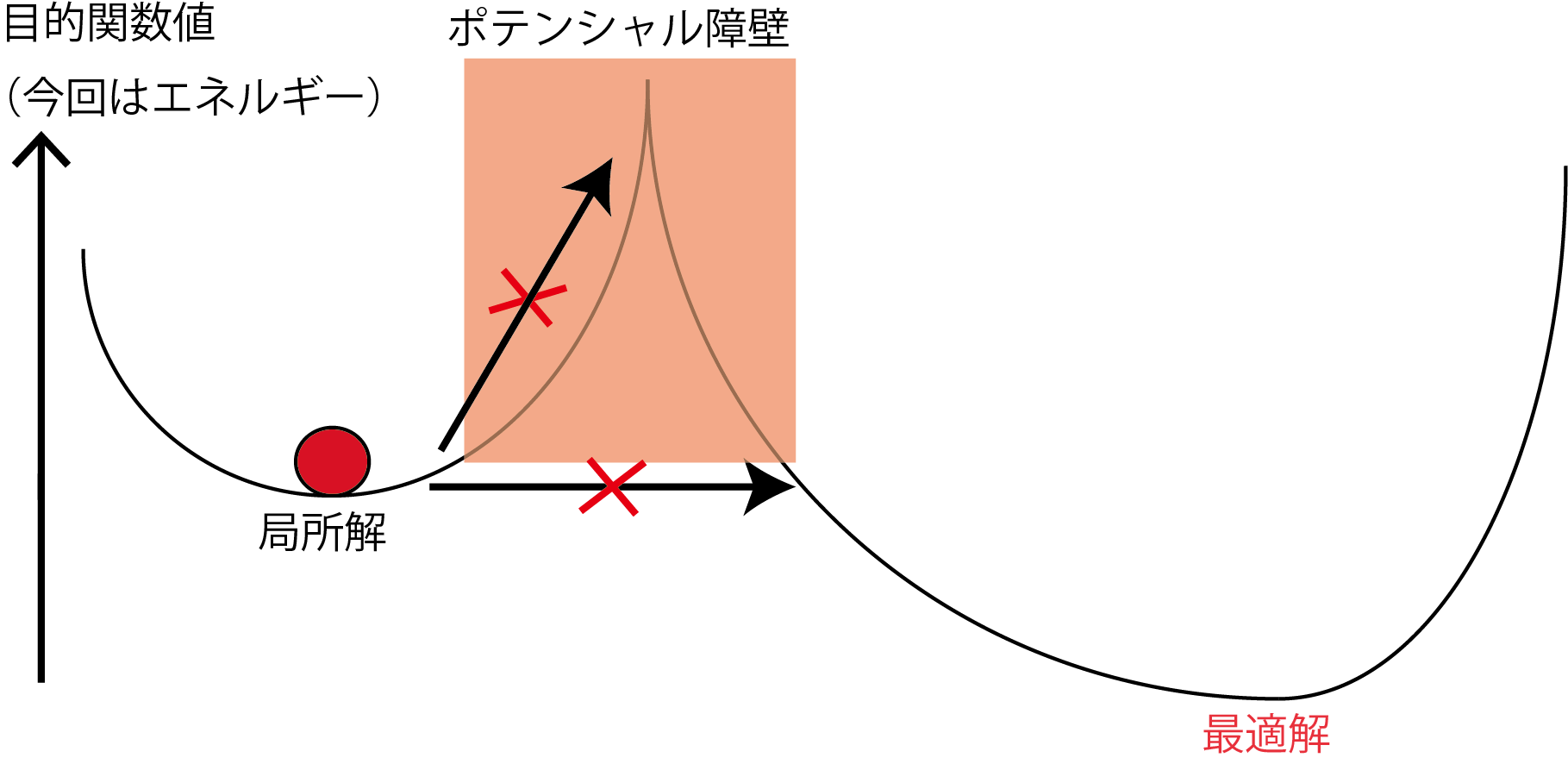
QAとSAが扱いづらい問題
以上を踏まえるとQAとSAは、局所解と最適解が厚くて高い壁で区切られているような問題では最適解を出力してくれる確率が著しく低くなりそうです。
決定的QAOAの条件を満たす中で、上記の条件を満たしてくれるようなハミルトニアンを作ります。
その為に、先ほどの式(3)の$H_{2\pi}$の部分が以下のような形になっているハミルトニアンを考えます。
$$
H_{2\pi} = 2\pi \tilde{\Delta}^2_t (\tilde{\Delta}_t - (N/2))^{2} + H _{2\pi}'
$$
$H_{2\pi}'$は全ての固有値が$2\pi$の倍数である、その他の任意のスピングラスハミルトニアンです。
係数に$2\pi$が付いているので、位相が全て揃うという条件は満たしています。
こうすることによって、$H_{2\pi}$はハミング距離$\Delta_t$が$ 0, N/2$であるような$|l \rangle$で最小値を取ります。
また、N個のqubitからN/2個のqubitを選ぶ組合せは${}_N C _{N/2}$個あるので、このような最小値をとる状態は沢山あることがわかります。
以上のことをグラフに図示すると以下のようになります。
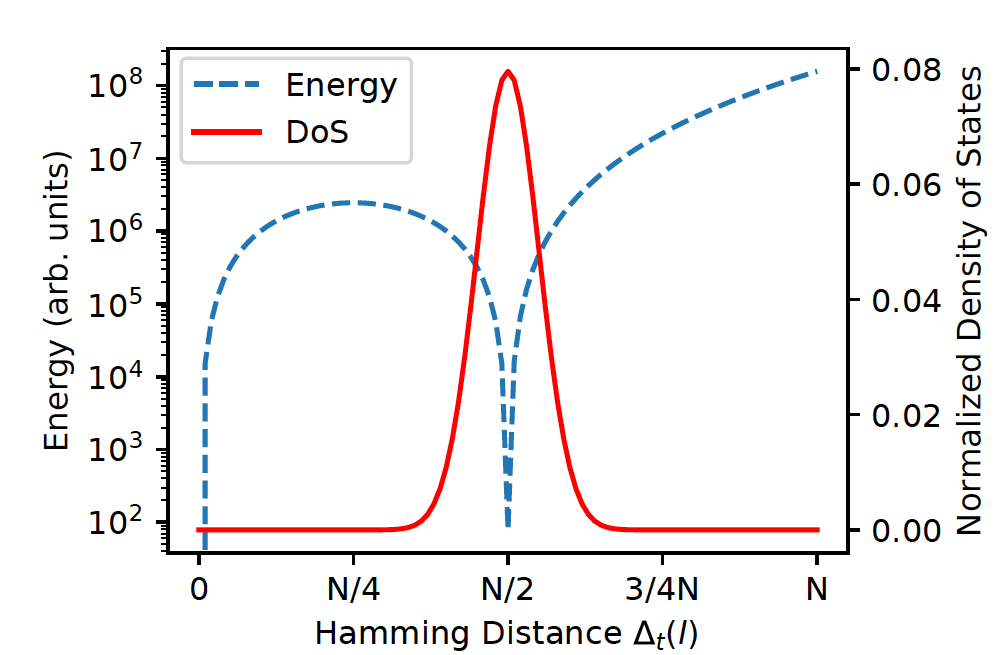
([1]より)
横軸に求めたい基底状態からのハミング距離、左縦軸が標準化した時の(3)式$H _{SG}$のエネルギー値、右縦軸が標準化した状態密度です。
また青の点線がエネルギーの分布で、赤線が状態密度になります。
図より、ハミング距離が0のところがエネルギー値が低い(最適解)一方で、N/2の箇所が次に小さく(局所解)なっており、そこに状態が多く重複しています。さらに、0とN/2の間は高く厚いポテンシャル障壁で遮られています。
よって、このハミルトニアンはQAでもSAでも解きにくいと考えられます。
(論文では、ハミルトニアンの固有状態の類似度の分布を用いた、より定量的な解析が行われています。)
考察
QAOAはQAA(量子断熱計算)をトロッター展開しただけのものですが、本質的にQAとSAとは異なるということがわかったと思います。
これはQAがゲート方式よりも劣っているということでは決してなく、アルゴリズムの本質にある物理的な性質が異なっているということです。
実務で使うSAを見ると、こういった場合でも局所解に陥ることのないように初期点を複数取るといった工夫などが行われています。
なので「扱いづらい」という風に記載しました。
また、決定的QAOAという考え方は面白かったです。
現在の$p=1$では、全ての波の位相が揃うというとても強い状況でのみ成り立ちます。
これを$p=2,3...$と増やしていけば問題のクラスは広がることになると思いますが、$p$をどれだけ増やせばどれくらい問題のクラスが広がるかということが定量的にわかると、応用の面でとても役に立ちますね。
ただ計算するのが大変だから、量子コンピュータにやらせる訳なので、$p=2$ですら計算するのもとても大変そうです。
これからQAOAの繰り返し回数pや、パラメータ$\gamma , \beta$などの特性がわかってくれば実用に向けて大きく前進しそうです。
トンネル効果など、ポテンシャルの厚みの基準がハミング距離で良いのかが気になりました。