【AtCoder】ABC102 D問題の解説【しゃくとり法】 #C++

AtCoder D問題で珍しく600点の問題が出たので解説してみました。
問題はこちら
→ https://beta.atcoder.jp/contests/abc102/tasks/arc100_b
解説をチラ見しましたがパフォーマンスはまだまだ改善できると思います。
アドバイス等あればコメントいただけると幸いです。

問題文

すぬけ君は、長さ N の整数列Aを持っています。
すぬけ君は A を3箇所で切って、4つの（空でない）連続する部分列 B, C, D, E に分解します。切る位置は自由に選ぶことができます。

ここで、整数列 B, C, D, E について、その要素の総和をそれぞれP, Q, R, Sとおきます。すぬけ君は、P, Q, R, S の最大値と最小値の差の絶対値が小さいほど嬉しいです。P, Q, R, S の最大値と最小値の差の絶対値としてあり得る最も小さい値を求めてください。

制約

$4 \leq N \leq 2 ×10^5$
$1 \leq A_i \leq 10^9$
入力はすべて整数である。

入力

入力は以下の標準入力から与えられる。

出力

$P, Q, R, S$ の最大値と最小値の差の絶対値としてあり得る最も小さい値を出力せよ。

方針

中央の仕切りを固定し、左右のそれぞれの数列について最適な仕切りを入れることを考えます。

はじめに、用語が多くなるためいくつか変数を定義しておきます(ここで定義した変数は後述するコード内でそのまま使われています。)

中央の仕切りの位置を mid_ix とし、mid_ix によって分断された左側の数列と右側の数列をそれぞれ L, R とします。
さらに、そのときの L と R の仕切りの位置を left_ix[mid_ix], right_ix[mid_ix]とします。

mid_ix $\in$ [1, N-3]
left_ix, right_ix $\in R^{N-1} $
left_ix[i], right_ix[i] $\in$ [0, mid_ix)

L, R について隣接する数列の和がなるべく近くなるように仕切りを入れましょう。しかし、$N$ の範囲が大きいため全探索では時間内に終わりません。

そこで、累積和を計算しておくことで $O(1)$ で特定の範囲の数列の和を計算することが出来ます。また、単調増加となるのでしゃくとり法を用いることが出来ます。

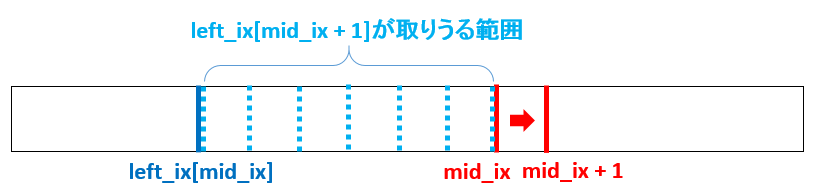
left_ix[mid_ix + 1]を求める際にleft_ix[mid_ix]から探索を始めればよいことから、しゃくとり法の問題に帰着できることが分かります。(同様のことをRに対しても行います。詳しくはコードを参照ください。)

しゃくとり法の詳しい解説はこちらの記事が分かりやすいです。
→ https://qiita.com/drken/items/ecd1a472d3a0e7db8dce

解説

Step0. 入力操作および変数の定義

主な変数は上記のとおりです。


#include<iostream>
#include<vector>
#include<algorithm>
#include<numeric>
#include<math.h>

#define REPS(i, a, b) for (int i = (a); i < (b); i++)
#define REP(i, n) for (int i = 0; i < (n); i++)

using namespace std;
using ll = long long;
const int mod = 1e9 + 7;

int N; // 要素数
cin >> N;

vector<ll> A(N); // 数列
vector<ll> sum_l2r(N), sum_r2l(N); // 累積和

// L,Rにおける仕切りの位置
vector<int> left_ix(N - 1), right_ix(N - 1);

Step1. 累積和の計算

累積和は左側から順に足したもの(sum_l2r)と、右側から順に足したもの(sum_r2l)の2種類計算しています。
これは、right_ixをleft_ixと同様に計算する際に必要になるためです。


sum_l2r[0] = 0, sum_r2l[0] = 0;
REP(i, N) {
    cin >> A[i];
    if (i > 0) {
        sum_l2r[i] += (sum_l2r[i - 1] + A[i]);
    }
    else sum_l2r[0] = A[0];
}
REP(i, N) {
    if (i > 0) {
        sum_r2l[i] += (sum_r2l[i - 1] + A[N - 1 - i]);
    }
    else sum_r2l[0] = A[N - 1];
}

Step2. L, Rにおける仕切りの位置の決定

中央の仕切りの位置を固定し、そのときのL, Rにおける最適な仕切りの位置を探索します。

このとき、仕切りの位置をずらしていくと最適な仕切りの位置までは隣接する数列の和の差 diff が小さくなることに注意します。
つまり、diff が大きくなるということは最適な仕切りの位置を通り過ぎているということなので、breakしてループを抜ける必要があります(これをやらないと計算量が最悪$O(N^2)$となり、TLEになります。)


// 真ん中の仕切りの位置をずらしたときの左右の仕切りの最適な位置を求める
// mid:[1]から[N-3]まで
REPS(mid_ix, 1, N - 2) 
{
    if (mid_ix > 1) {
        // 数列Lについて
        left_ix[mid_ix] = left_ix[mid_ix - 1]; // 引継ぎ

        ll left_diff = abs(sum_l2r[mid_ix] - 2 * sum_l2r[left_ix[mid_ix - 1]]); // 2つの数列の和の差を計算
        REPS(ix, left_ix[mid_ix - 1] + 1, mid_ix) {
            if (left_diff > abs(sum_l2r[mid_ix] - 2*sum_l2r[ix])) {
                left_ix[mid_ix] = ix;
                left_diff = abs(sum_l2r[mid_ix] - 2 * sum_l2r[ix]);
            }
            else break; // これがないとTLE!!
        }

        // 数列Rについて
        right_ix[mid_ix] = right_ix[mid_ix - 1]; // 引継ぎ

        ll right_diff = abs(sum_r2l[mid_ix] - 2 * sum_r2l[right_ix[mid_ix - 1]]); // 2つの数列の和の差を計算
        REPS(ix, right_ix[mid_ix - 1] + 1, mid_ix) {
            if (right_diff > abs(sum_r2l[mid_ix] - 2 * sum_r2l[ix])) {
                right_ix[mid_ix] = ix;
                right_diff = abs(sum_r2l[mid_ix] - 2 * sum_r2l[ix]);
            }
            else break; // これがないとTLE!!
        }

    }
    else {
        // mid_ix = 1のときは強制的に決まる
        left_ix[1] = 0;
        right_ix[1] = 0;
    }
}

Step3. 中央の仕切りの位置の決定

Step2で中央の仕切りの位置を全探索し、すべてのleft_ix, right_ixが求まりました。
あとは愚直に 4つの数列和の最大値と最小値を求め、それらの差が最も小さくなる値を探せばOKです。

left_ixとright_ixは順序が逆になっているので気を付けてください。
(left_ix[i]はright_ix[N - 2 - i]に対応しています。)


ll ans = mod;
REPS(mid_ix, 1, N - 2)
{
    ll left_min = min(sum_l2r[mid_ix] - sum_l2r[left_ix[mid_ix]], sum_l2r[left_ix[mid_ix]]);
    ll left_max = max(sum_l2r[mid_ix] - sum_l2r[left_ix[mid_ix]], sum_l2r[left_ix[mid_ix]]);

    ll right_min = min(sum_r2l[N - 2 - mid_ix] - sum_r2l[right_ix[N - 2 - mid_ix]], sum_r2l[right_ix[N - 2 - mid_ix]]);
    ll right_max = max(sum_r2l[N - 2 - mid_ix] - sum_r2l[right_ix[N - 2 - mid_ix]], sum_r2l[right_ix[N - 2 - mid_ix]]);

    ans = min(max(left_max, right_max) - min(left_min, right_min), ans);
}
cout << ans << endl;