DeepLearningを確率的に扱えるモジュール、Edwardライブラリについてお話をしたいと思います。
ここで、学習するのはネットワークの重みではなく、重みを生成する分布のパラメータです。分布が正規分布であれば、平均と分散を求めることになります。
何が嬉しいのか?
推論時は各分布から重みを1つサンプリングして推論するので、1つの入力に対して出力は一意に定まりません。1つの入力に対して複数の重みのサンプリングを行い、得た出力から平均と分散を求めることができます。
\mu = \frac{1}{N}\Sigma_i^NP(y_i|x_i, w_i) \\
\sigma^2 = \frac{1}{N}\Sigma_i^N(x_i - \mu)^2
分散がわかるということは推論に対する信頼度を測ることができるというわけです。特に回帰問題とかは出力が確率値ではないことがほとんどなので、分散もわかると何かと便利な気がします。
また、サンプリング数が多ければ多いほど右辺は左辺の式により近づきます。
P(y|x, w) ≃ \frac{1}{N}\Sigma_i^NP(y_i|x_i, w_i)
というわけでネットワークの重みの分布を学習するEdwardライブラリのサンプルコードをベースにして、回帰問題を解いてみたいと思います。
Edwardを手に入れる
ライブラリはgithubにあがっており、サンプルコードもたくさんあるため、とりあえず手を動かしてみる上での敷居はかなり低いです。
tensorflowを内部で用いていますので、インストールの際にはtensorflowも必要になります。
今回はexamples/bayesian_nn.pyをベースにコードをリライトしていきます。
サンプルコードをリライトする
まずは学習するためのコードです。CPUだけの環境でも実時間で学習が終わります。3分くらいだったと思います。
from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
import edward as ed
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from edward.models import Normal
def build_toy_dataset(N=100, noise_std=0.05):
D = 1
X = np.linspace(-np.pi, np.pi, num=N)
y = np.cos(X) + np.random.normal(0, noise_std, size=N)
X = X / np.pi
X = X.reshape((N, D))
return X, y
def neural_network(X, W_0, W_1, W_2, b_0, b_1, b_2):
h = tf.tanh(tf.matmul(X, W_0) + b_0)
h = tf.tanh(tf.matmul(h, W_1) + b_1)
h = tf.matmul(h, W_2) + b_2
return tf.reshape(h, [-1])
ed.set_seed(42)
N = 40 # number of data points
D = 1 # number of features
X_train, y_train = build_toy_dataset(N)
# ネットワークのパラメータの分布
with tf.name_scope("model"):
W_0 = Normal(loc=tf.zeros([D, 10]), scale=tf.ones([D, 10]), name="W_0")
W_1 = Normal(loc=tf.zeros([10, 10]), scale=tf.ones([10, 10]), name="W_1")
W_2 = Normal(loc=tf.zeros([10, 1]), scale=tf.ones([10, 1]), name="W_2")
b_0 = Normal(loc=tf.zeros(10), scale=tf.ones(10), name="b_0")
b_1 = Normal(loc=tf.zeros(10), scale=tf.ones(10), name="b_1")
b_2 = Normal(loc=tf.zeros(1), scale=tf.ones(1), name="b_2")
X = tf.placeholder(tf.float32, [N, D], name="X")
y = Normal(loc=neural_network(X, W_0, W_1, W_2, b_0, b_1, b_2), scale=0.1 * tf.ones(N), name="y")
# 重み変数の定義
# qW_0やqb_0が実際に最適化されるので、こいつらからサンプリングすれば良い
with tf.name_scope("posterior"):
with tf.name_scope("qW_0"):
qW_0 = Normal(loc=tf.Variable(tf.random_normal([D, 10]), name="loc"),
scale=tf.nn.softplus(
tf.Variable(tf.random_normal([D, 10]), name="scale")))
with tf.name_scope("qW_1"):
qW_1 = Normal(loc=tf.Variable(tf.random_normal([10, 10]), name="loc"),
scale=tf.nn.softplus(
tf.Variable(tf.random_normal([10, 10]), name="scale")))
with tf.name_scope("qW_2"):
qW_2 = Normal(loc=tf.Variable(tf.random_normal([10, 1]), name="loc"),
scale=tf.nn.softplus(
tf.Variable(tf.random_normal([10, 1]), name="scale")))
with tf.name_scope("qb_0"):
qb_0 = Normal(loc=tf.Variable(tf.random_normal([10]), name="loc"),
scale=tf.nn.softplus(
tf.Variable(tf.random_normal([10]), name="scale")))
with tf.name_scope("qb_1"):
qb_1 = Normal(loc=tf.Variable(tf.random_normal([10]), name="loc"),
scale=tf.nn.softplus(
tf.Variable(tf.random_normal([10]), name="scale")))
with tf.name_scope("qb_2"):
qb_2 = Normal(loc=tf.Variable(tf.random_normal([1]), name="loc"),
scale=tf.nn.softplus(
tf.Variable(tf.random_normal([1]), name="scale")))
inference = ed.KLqp({W_0: qW_0, b_0: qb_0,
W_1: qW_1, b_1: qb_1,
W_2: qW_2, b_2: qb_2}, data={X: X_train, y: y_train})
inference.run(logdir='log', n_iter=10000)
# モデル保存
sess = ed.get_session()
saver = tf.train.Saver()
saver.save(sess, "test_saver")
学習が終わって、モデルが無事保存されたことを確認したら、次に推論をさせます。推論のコードは学習のコードと似ている部分があるので、その差分だけを示します。
"""
bayseian_nn_train.pyのモデル保存を行う部分のコードをコメントアウトした後に、以下のコードを貼り付ける。
"""
# モデル読み込み
sess = ed.get_session()
saver = tf.train.Saver()
saver.restore(sess, "test_saver")
# Build samples from inferred posterior.
n_samples = 50
inputs = np.linspace(-1, 1, num=200, dtype=np.float32).reshape((200, 1))
preds = tf.stack([neural_network(inputs, qW_0.sample(), qW_1.sample(), qW_2.sample(),
qb_0.sample(), qb_1.sample(), qb_2.sample())
for _ in range(n_samples)])
all_outputs = preds.eval()
for n in range(n_samples):
outputs = all_outputs[n, :]
plt.plot(inputs, outputs, color='blue')
plt.plot(X_train.ravel(), y_train.ravel(), color='red')
plt.show()
結果をプロットする
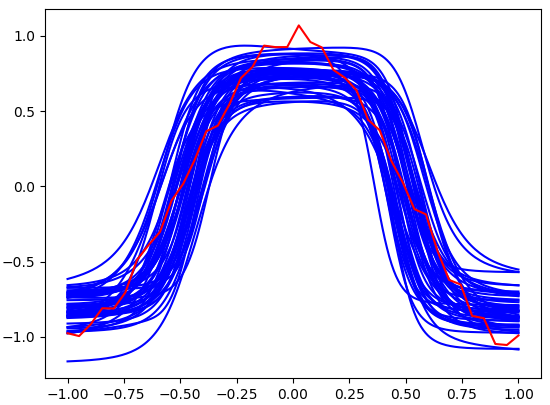
学習された分布から重みをそれぞれ50個ずつサンプリングし、描画したものがこちらになります。赤い線が教師信号の関数で、50本ある青い線が推論結果です。ある程度フィティングできていることがわかります。
理論的なお話
$x$から$y$を推定したい(画像$x$から文字$y$を推定したい的な感じ)と考えたときに、パラメータ$w$を用いて数式を定義します、あとは大量の学習データ($x$と$y$とのペア)から$w$の取りうる範囲を分布として求めることです。
数学的には以下の確率分布を求めたいという話になります。
P(W|X, Y)
$X$, $Y$, $W$は$x$, $y$, $W$の集合です。
でも、これをダイレクトに求めるのはすごく難しいというかできないので、近似計算を行います。具体的に何をするのかというと、パラメータ$\theta$を用いて$Q_{\theta}(W)$を定義し、この関数を$P(W|X, Y)$に近づけることを目指します。
この"$Q_{\theta}(W)$を定義"というのが、bayseian_nn_train.pyのwith tf.name_scope("posterior"):と書かれている部分の実装に対応します。つまり今回の場合、パラメータ$\theta$は正規分布の平均や分散に対応すると考えることができます。
損失関数はKL特徴量です。単純な話が、2つの分布の距離のようなもの(厳密には距離ではない)が測れます。厳密には距離ではないのですが、2つの分布が似ていれば値は小さく、分布が似ていなければ値は大きくなるので、このKL特徴量を最適化し、その結果得られた$\theta$を使えば、推論ができるというわけです。
inference = ed.KLqp({W_0: qW_0, b_0: qb_0,
W_1: qW_1, b_1: qb_1,
W_2: qW_2, b_2: qb_2}, data={X: X_train, y: y_train})
上の式を数式で書き表すと以下になります。
KL(Q_{\theta}(W) | P(W|X, Y))
上式は式展開により、以下の式で書き表すことができます。
KL(Q_{\theta}(W) | P(W|X, Y)) \\
= \int{Q_{\theta}(W)log(\frac{Q_{\theta}(W)}{P(W|X, Y)})}dw \\
= logP(Y|X) - \int{Q_{\theta}(W)logP(Y|X, W)dw} + KL(Q_{\theta}(W)|P(W))
3つの項が出てきましたね。左から順に見ていきたいと思います。
まず第1項$logP(Y|X)$には重み$W$がないので、最適化する上でここは定数項です。なので、消去してもかまいません。
次に第2項$-\int{Q_{\theta}(W)logP(Y|X, W)dw}$を見ていきます。ここが一番やっかいですが、一番重要な部分です。仮に$Q_{\theta}(W)$がかなり正しく真の分布の形状を表せているとします。このとき、$Q_{\theta}(W)$からいくつか$W$をサンプリングし、$P(Y|X, W)$を計算したらどうなるでしょうか。$X$と$Y$はデータセットなので、かなり高い確率値を得るはずです。すなわち、ある$W$に対して$Q_{\theta}(W)$->大、$P(Y|X, W)$->大となります。なので、分布が近いほど値が大きくなるのですが、最後に-1をかけることにより、最小化を目指すことで最適化されるようになります。
$Q_{\theta}(W)$がでたらめな分布であれば、ある$W$に対して$Q_{\theta}(W)$か大きいのに$P(Y|X, W)$が小さいため、第2項全体としては値が大きくなります。
最後に第3項$KL(Q_{\theta}(W)|P(W))$についてです。これは正規化項のはたらきをします。要は事前分布からあまり遠ざかるなよ? と言っているわけです。
順伝搬時の工夫
ネットワークの順伝搬時に、いくつかのパラメータ(正規分布の場合は平均と分散)を用いて、サンプリングをする箇所があるわけですが、サンプリングをすると微分ができなくなるという問題があります。真値との誤差による信号をサンプリングした箇所より前に伝搬させることができないわけです。
今回の場合ですと、重みは分布からサンプリングしているので、重みの更新が逆誤差伝搬法ではできませんし、
y = Normal(loc=neural_network(X, W_0, W_1, W_2, b_0, b_1, b_2), scale=0.1 * tf.ones(N), name="y")
とyを推論する際の正規分布の平均はネットワークの出力の値を用いて、そこからyをサンプリングするわけですから、この式よりも前には誤差が伝搬しません。
ですが、これに対する対処法はすでに考案されており、VAEなどでも取り入れられております。
正規分布を例に説明してみます。正規分布の平均$\mu$および分散$\sigma^2$からサンプリングすると学習ができなくなるので、0~1までの値をランダムに取る$\epsilon$を用いて、$\mu+\epsilon\sigma$を計算し、これを次の層への入力として渡します。サンプリングの前後では微分不可能だったのが、この対処法により微分可能になるので、誤差がちゃんと伝搬するというわけです。
ちなみに、出力層においてscale=0.1 * tf.ones(N)なので、分散(標準偏差)は固定になっているのですが、ここもDeep Learningで推定させることも可能です。ただ、現在のネットワークに、さらに分散(標準偏差)を推定させる部分を付け足す必要があるので計算量は増えます。
さいごに
冒頭の推論の信頼度を測る、という意味では分散(標準偏差)を固定にしてはダメでしたね。ちゃんと分散も推定させる必要がありました。