はじめに
力の作用線・作用点再考
前章「投球の力学の基礎(2) -ボールに作用する力と力の作用線:剛体の回転の力学-」で,ボールに作用するトルクは,力の作用線・作用点で記述される力のモーメントと,ねじりモーメントに分解できることを示した.
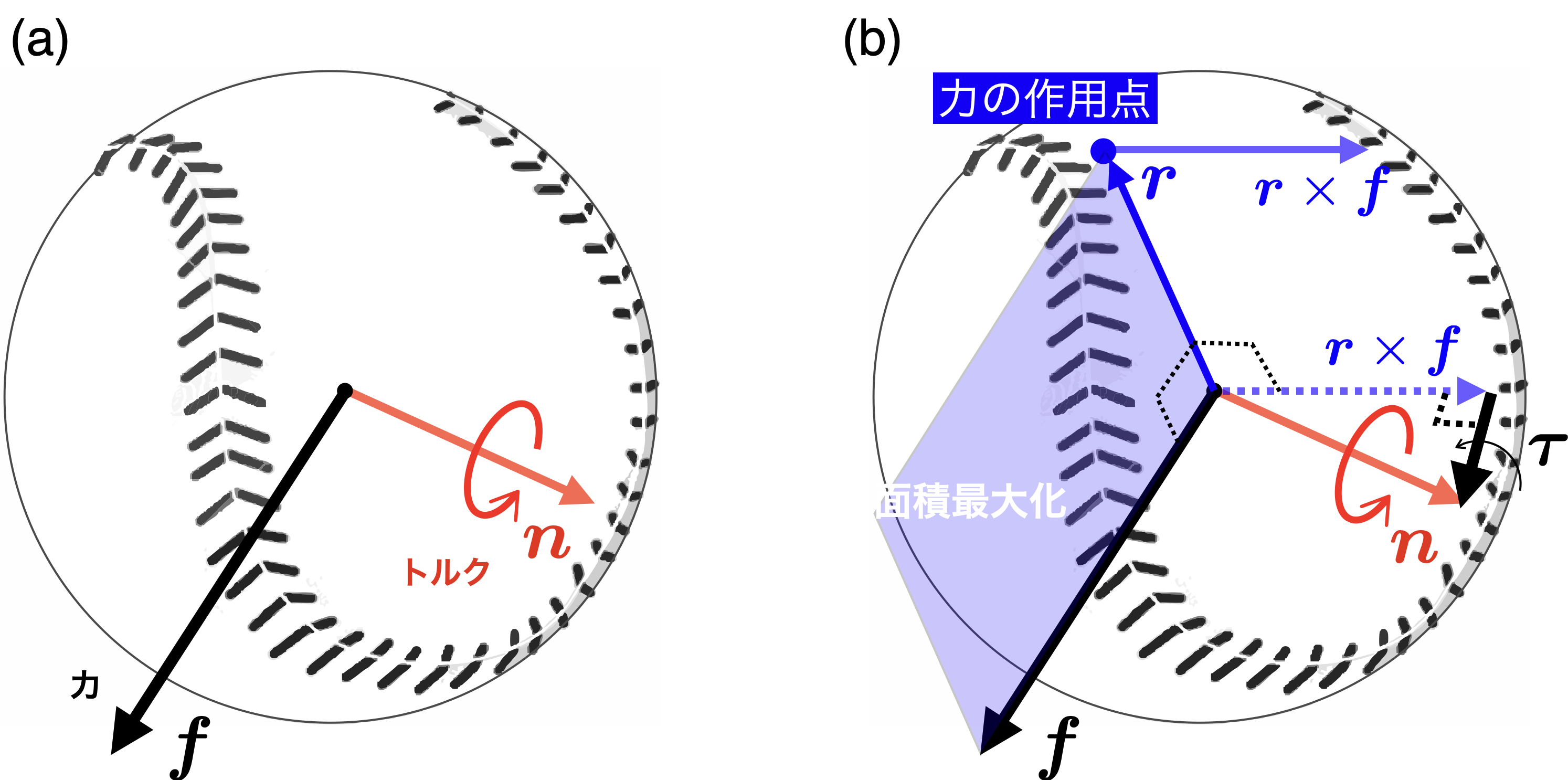
図1:(a)ボールに作用する力fとトルクn.(b)力のモーメント
そこでで述べなかったが,力の作用線・作用点のもう一つの本来の意味は,図1(a)のボールに作用する総和のトルク$n$を,「できるだけ一つの(ボールに作用する)力のモーメントで記述する」際の,力が作用する位置ベクトルを意味する.
ボールには力ベクトル$\boldsymbol{f}$とトルクベクトル$\boldsymbol{n}$が作用する.しかし,この時点で力$\boldsymbol{f}$がどこに作用しているかは不明である.図1(a)のように,とりあえずボールの中心に力$\boldsymbol{f}$とトルク$\boldsymbol{n}$が作用するしか表現しようがない.しかし,力がどこに作用しているかがわかれば,ボールの回転の操り制御の戦略が見えてくる.
そこでここでは,剛体の運動学における瞬間回転軸(instantaneous screw axis)とのアナロジーで力の作用点の意味を考える.
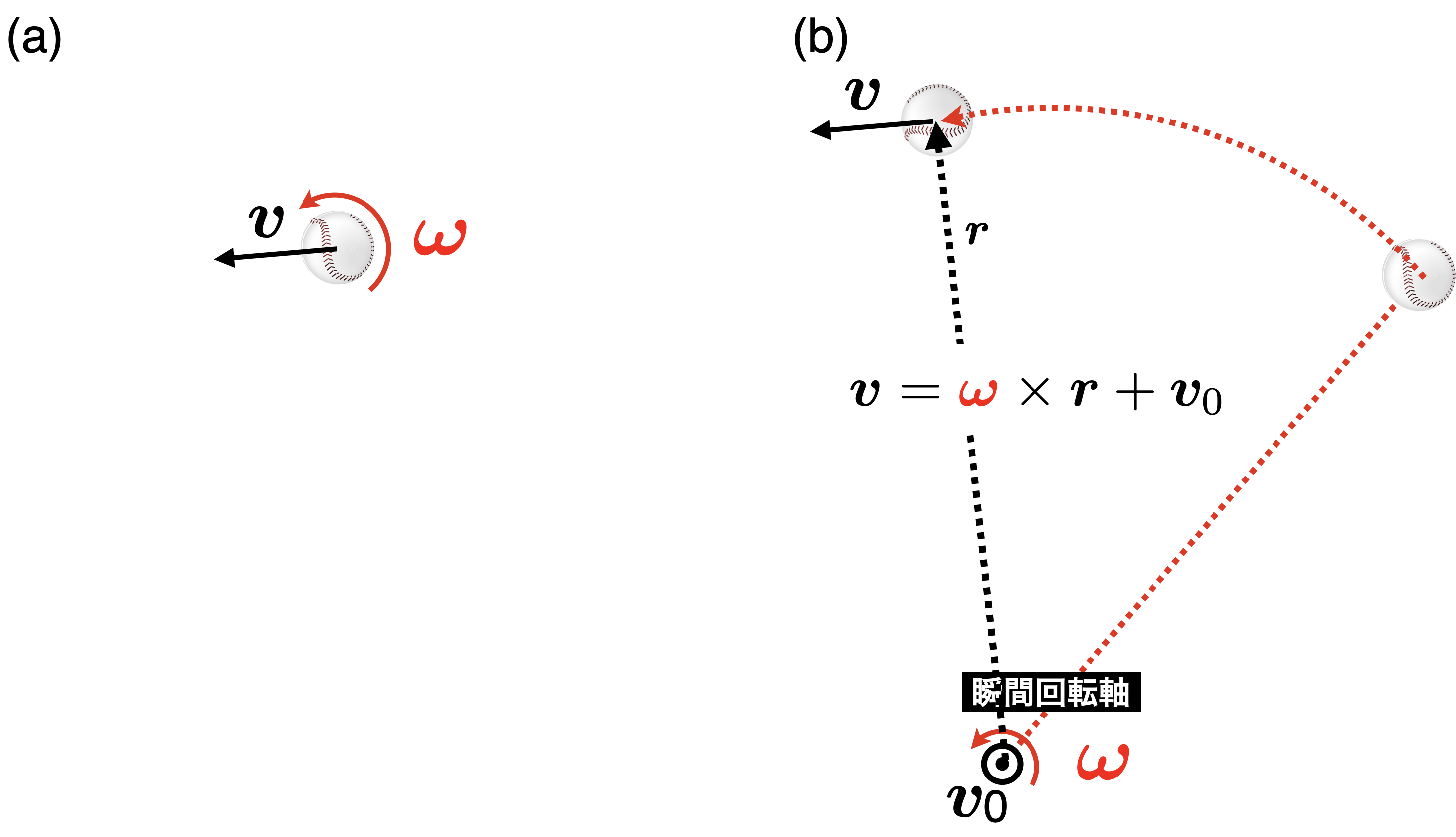
図2:瞬間回転軸
剛体の瞬間回転軸とは,通常ボール(剛体)の運動を速度$v$と角速度$\omega$のペアで記述するのだが(図1(a)),図1(b)のように,剛体の運動を(できるだけ)ひとつの回転運動だけで記述する際の,回転軸を意味する.これは点ではないことに注意されたい.瞬間回転軸の詳細は過去のnote記事(多関節運動の代表値 多体系における瞬間回転軸の意味)や剛体運動の代表値 剛体の瞬間回転軸などを参照していただきたい.
運動学の瞬間回転軸と同様に,力学バージョンとして,「剛体に作用するトルクを一つの力のモーメント」で記述することを考える(図1(b)).
ここで,力ベクトル$\boldsymbol{f}$が作用する位置ベクトルを$r$とすると,力のモーメントは
$$
\boldsymbol{r} \times \boldsymbol{f}
$$
と書け,できるだけこの一つのモーメントで$\boldsymbol{n}$記述したいので,$\boldsymbol{r} \times \boldsymbol{f}$を最大化することを考えると,力が作用する位置が$\boldsymbol{r}$となる.どのようにして計算するかはnote記事「剛体の力学の代表値 力の作用線」などを参照していただきたい.
このとき,たとえ示指だけでボールを押していても,力は面接触しているので,無数の力が指とボール間に作用していると考えるのが良い.力がどこに作用しているかを一つの力で記述したのが,力の作用点である.
ただし,COPとは異なる.ここは注意をされたい.COPを計算すると(曲面を持つ球体では,そもそも計算が困難)も力の作用点と似たような位置を示すことになるだろうが,COPは圧力(ボールの表面の法線方向の力)の代表値(重心)である.作用する力の面の向きの取り方が異なることは,前章で示した.力の作用点は,ボールに作用する力ベクトルに対して垂直な方向を集めた重心であるが,COPはボール表面の面に対しての重心であり,COPは一つのモーメントでできるだけトルク$n$表そうとしているわけではないので,同じように力のモーメントを計算しても,それは最大になるわけではない.
このように力の作用点は,ボールの力学を3次元空間で可視化するツールとなる.ただし,都合よく,ひとつの$\boldsymbol{r}\times \boldsymbol{f}$だけでトルク$\boldsymbol{n}$を記述できず,力ベクトル$\boldsymbol{f}$と同じ方向を向くねじりモーメント$\tau$も作用するので,
$$
\boldsymbol{n} = \boldsymbol{r} \times \boldsymbol{f} + \boldsymbol{\tau}
$$
となる.これで力がどこに作用するかがわかれば,ボールにどのような回転を与えるかがわかりやすくなる.
なお,イメージできると思うが,ストレートの投球のように示指や中指で与えるねじりモーメントは小さい.しかし,ねじりモーメント$\tau$は握り方によっては大きくなり,複数の指でピンチング(把持)で操作する変化球では大きくなる傾向にある.離れた位置の指をもちいればねじりモーメントは簡単に与えられる.
もう一度考えてみてほしい,ボールに作用する力やトルクのグラフを眺めてみても,ボールにどのような力学が作用しているかを理解するのは困難である.ボールの中心に力ベクトルやトルクベクトルの2つを描くことはできても,そのメカニズムを2つのベクトルを描いても理解するには厳しい.そこで,力の作用線や作用点を考えることに意味がある.
なお,力の作用線とは,力ベクトルがボールのどこに作用しているかを示すわけだが,たとえ複数の指でボールを押しても,示すことができる.変化球のように,離れた複数の指でボールを操作する場合,力の作用点は恐らくどこかの指の近くに力が作用している.たとえ離れていた複数の指で押していても,重要な情報を与えてくれる.
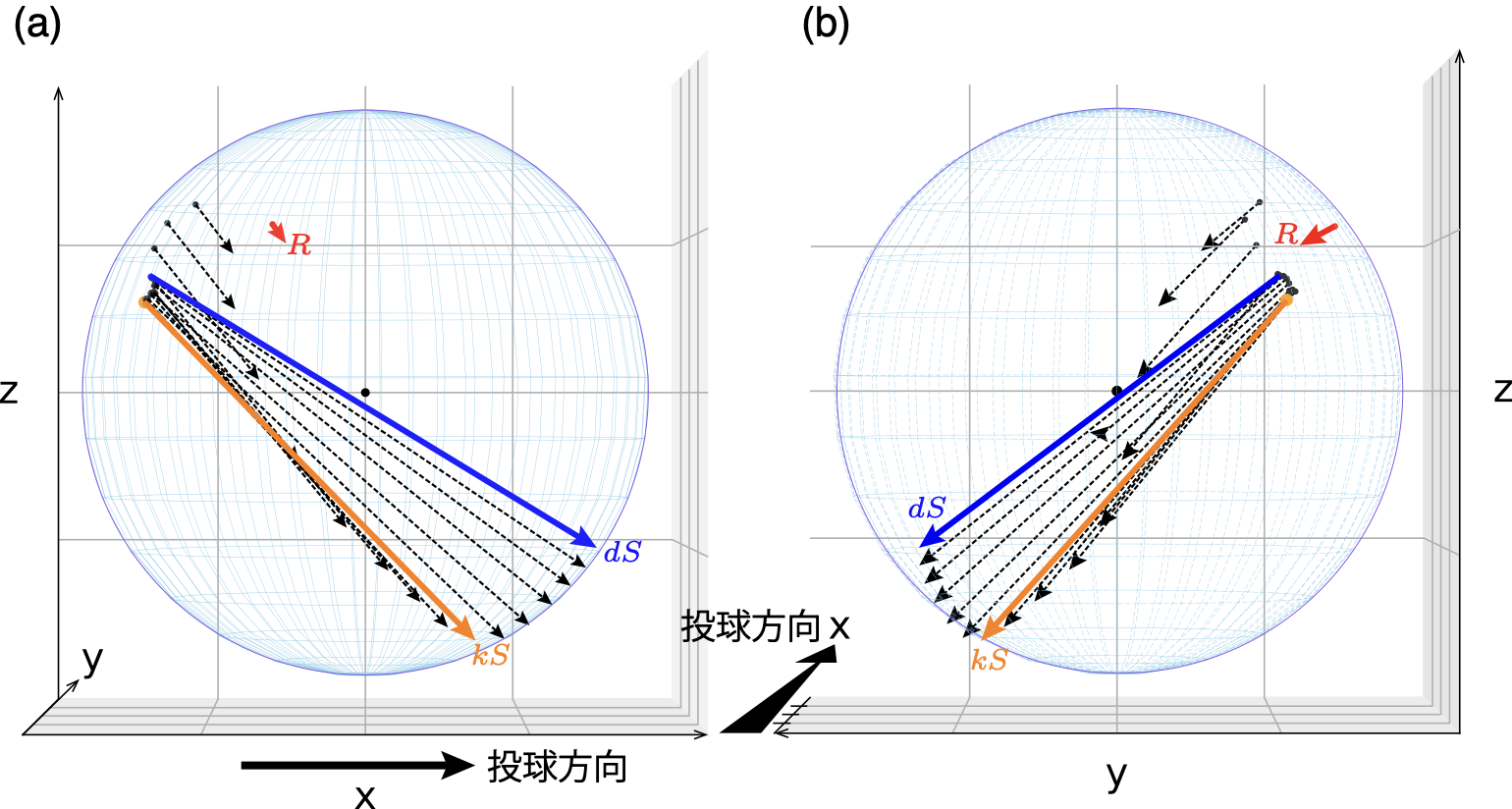
図3:ストレート(4 seam)の投球時のリリース前のボールに作用する力.
(a)真横.(b)真後ろからの投影図
図3には,ストレートの投球を行った際の,リリース前のおおよそ15ms前ぐらいからリリースまでの,ボールに作用する力ベクトル$\boldsymbol{f}$を,力の作用点に描いたものである.前章の図1の動力学的回転開始に相当するのが,この図3の青線(dS)で,バックスピン開始(運動学的回転開始: kS)に相当するのが,黄色の線となる.
詳しい説明は,次章で行うが,ストレートの投球のバックスピンの制御中,ほぼ同じ位置に力が作用している.つまり,ロボットのマニュピレーションで言われるところの,転がり制御を行っている.このことは,投球の制御やメカニズムを考えるうえで極めて重要な意味を持つ.