投球の力学メカニズム(6) −スピン回転軸と力発揮の効率−

はじめに

復習：身体のスイング軸の傾きがスピン回転軸を定める

前章：「スピン回転軸は向心力で定まる」で，「真後ろ」から見た身体全体のスイング（振り）の傾きが鉛直に近いほど（いわゆる「縦振り」に近いほど），ボールの回転軸を真横にしようとする力が作用し，「効率的なボールの回転」に結びつくことを述べた（図１参照）．

具体的には，ボールの曲率中心（ボールの軌跡の運動を一つの回転運動で記述したときの中心）からボールまでを結んだ直線を可変長振子とし（図１参照），図１左の真後ろから見たこの振り子の傾きが大きいほど，ボールの回転軸の傾きが大きくなる．図１ではほぼ同じ球速（約135 km/h）のA,Bの二つの投球例を示し，右側の真上から見た図でもボールの回転軸は真横から傾くことを示した．

そこで，ヒト側の都合を考えず，ボールの回転軸を真横にするほうが効率良い揚力¹を得られるという観点では，身体側の回転運動は「縦振り（振り子の傾きが鉛直に近いスイング）」に近づける方が良いと考えられる．

図1：可変長振子の傾きがボール回転軸の傾きに影響する（左：真後ろ，右：真上）．A,Bの投球例の比較．

スイング軸と効率

このように前章では，身体側のスイング（回転）軸が，ボールの回転軸にどのような影響を与えるか，その力学メカニズムについて述べ，回転軸の傾きや方向などで評価した．ここでは，それを力発揮の効率として評価する方法を考えたい．

（機械＋ヒト）系の最適化

たとえばボールを遠くに投げる際，ヒトは必ずしも物理的に最適な方向に力発揮ができるわけではない．

もし，ボールをできるだけ遠くに投げたいという「目的」（距離最大化）がある場合，マシンのようにどの角度に対しても同じように力発揮ができるなら，45度の方向に投射すればよいのだが²，ヒトは投げる角度によって発揮できる力が異なるので必ずしも45度が最適な投擲結果になるとは限らない．

このような「機械系の最適化」（45度に投擲）が，そのヒトの能力に応じた「ヒト＋機械系の最適化」と異なることは，身体運動ではよくあることである．しかし，トレーニングや学習によって，機械的に最適な方向に次第に進化することもある．投球の話に戻すと，可変長振子の傾きが大きいことは必ずしも悪いことでないが，恐らく競技力が向上するにつれ，個人間のゆらぎも大きいだろうが，平均的にその傾きは小さくなる方向に作用（進化）するだろう．

図２：ヒトによる投擲最大化において45°は最適とは限らない．

次に，このような観点も踏まえて，身体の回転軸の傾きが，「ボールに作用する力に対してあたえる影響」を考える．

無駄な力発揮？

前章で，投球時のボールに作用する力は，互いに直交する「投球方向の力」と「向心力」³に分解できることを述べた．ボールに作用する力は，ボールの回転開始（動力学的回転開始）時に最大化するが，その時，投球方向に作用する力よりも，向心力のほうがやや大きい．また，向心力は回転を維持するために必要な力で，ボールを加速するためにも間接的に必要な力で，大きな「向心力」が必ず作用する．これはヒトの都合で致し方ない．

図３：ボールに作用する力は，互いに直交する「投球方向の力」と「向心力」に分解される．

なお，以下の議論では，ボールに作用する力の意味を理解しやすくするために，真上（top view），真後（back view），真横（side view）に分けて考える．

力のy成分（真後：yz平面）

図４のように，投球（$x$）方向に向かって真後ろ（$-x$）からボールの運動を眺めると，ボールに作用する力は向心力とほぼ等しく重なって見える．これは投球方向の力が紙面の奥（$x$）方向を向いているためである．そこで，「yz平面における」ボールに作用する力の水平成分は，ほぼ$y$成分と一致し，ボールに作用する力と向心力はほぼ一致する．

また，これまでの議論から，特にこの「ボールに作用する力$\boldsymbol{f}$の$y$成分：$f_y$」は，これまでの議論のように，ボールの回転軸を傾けることになるため，以降$f_y$をあまり大きくしたくない力成分と仮定する．

図４から，図１で示した右側に示したBの投球例のように可変長振子の傾きが大きいと，$f_y$（ボールに作用する力$\boldsymbol{f}$の$y$成分）が大きくなる．

仮に縦振りが望ましい投球スイングとすると，$f_y$を小さくしたい．また，ヒトを含まない機械系の立場からすると，$f_y$は無駄な力となる．

図４：真後ろから見た，ボールに作用るする力の水平成分．投球方向の力は前方向きで見えない．
    　つまり，真後ろから見た場合，「ボールに作用する力」 ≒ 「向心力」

力のy成分（真上：xy平面）

図５のように，真上（$z$）方向から投球を眺めると，図４とは異なり，投球方向に作用する力が見える．なお，投球方向の力は，完全に$x$方向を向くわけではないので，ボールに作用する力$\boldsymbol{f}$の$y$成分$f_y$と投球方向の力$\boldsymbol{f}_v$は完全に直交するわけではないが，ほぼ直交すると考えて良い．

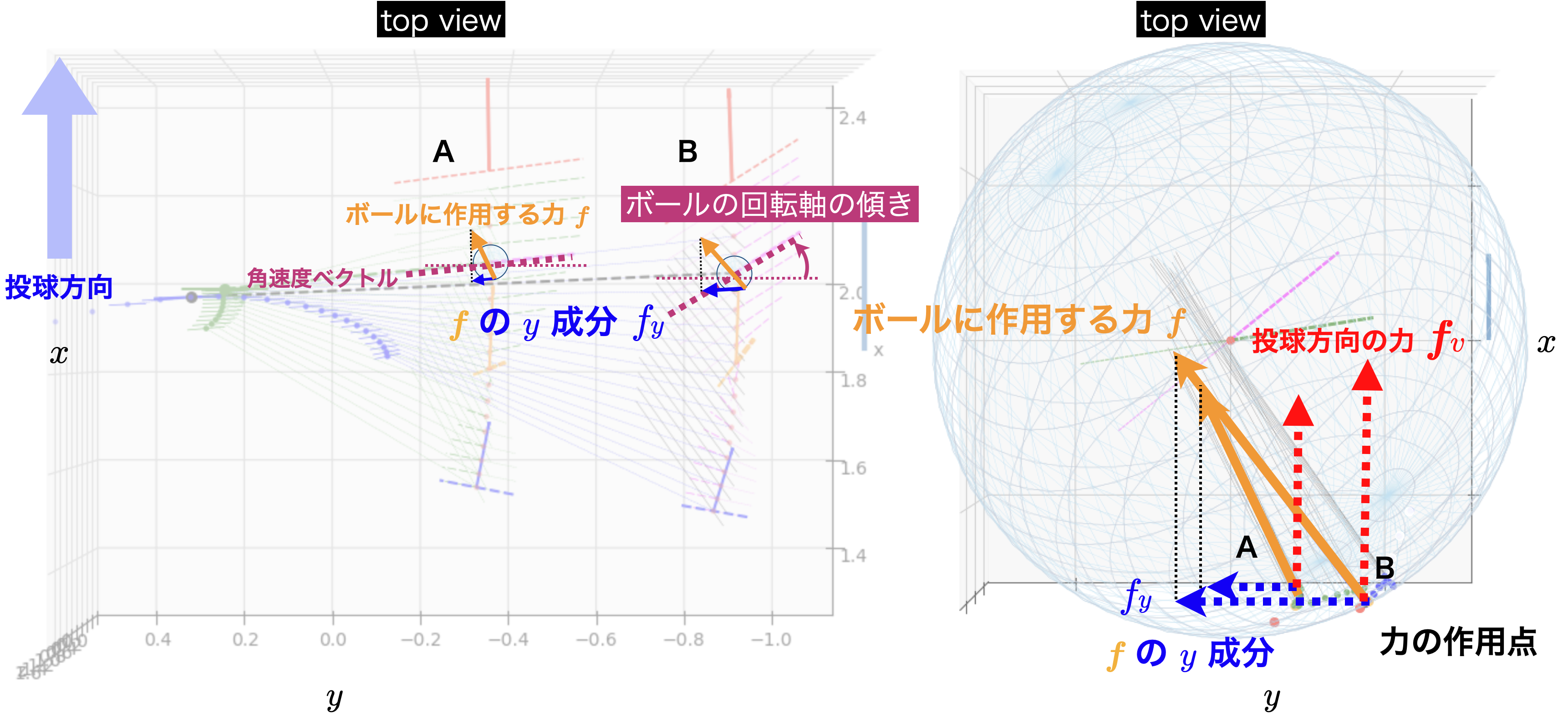
図５：真上から眺めたボールに作用する力の水平成分．

軸回転方向の効率

ボールの回転軸の方向は，揚力と関係することを述べた．

また，前述のようにヒトを含まない機械系の立場からすると，$y$方向に作用する力$f_y$は揚力向上においては無駄な力発揮である．そこで，機械系だけの立場で以下のように揚力に関係する「ボールの回転軸」に関係する力発揮の効率$\eta_y$

$$
\eta_y = \frac{|\boldsymbol{f}| - f_y}{|\boldsymbol{f}|}
$$

を定義する．

ここで，$|\boldsymbol{f}|$はヒトがボールに作用する力（オレンジ色）の大きさである．

ここで述べる効率とは伝達効率ではなく，ヒトの都合は考慮せず，揚力向上の目的に対する力発揮の「無駄の少なさ」という効率である．

図６に，前章から取り上げている図４の左右の投球例の効率$\eta_y$を示す．これを前章の図12の右に示した可変長振子の傾き角度と比較すると，ほぼ同じような結果を示している．すなわち，回転軸を真横にする揚力発生という観点では，左の投手は回転制御フェーズ全体で効率が良い．

身体側の鉛直軸まわりの回転成分を「横振り」と呼ぶと，これは，いわゆる可変長振子（身体のスイング）の「縦振り」ではなく「横振り」成分が多くなり，向心力の水平成分が大きくなっているためと考えられる．

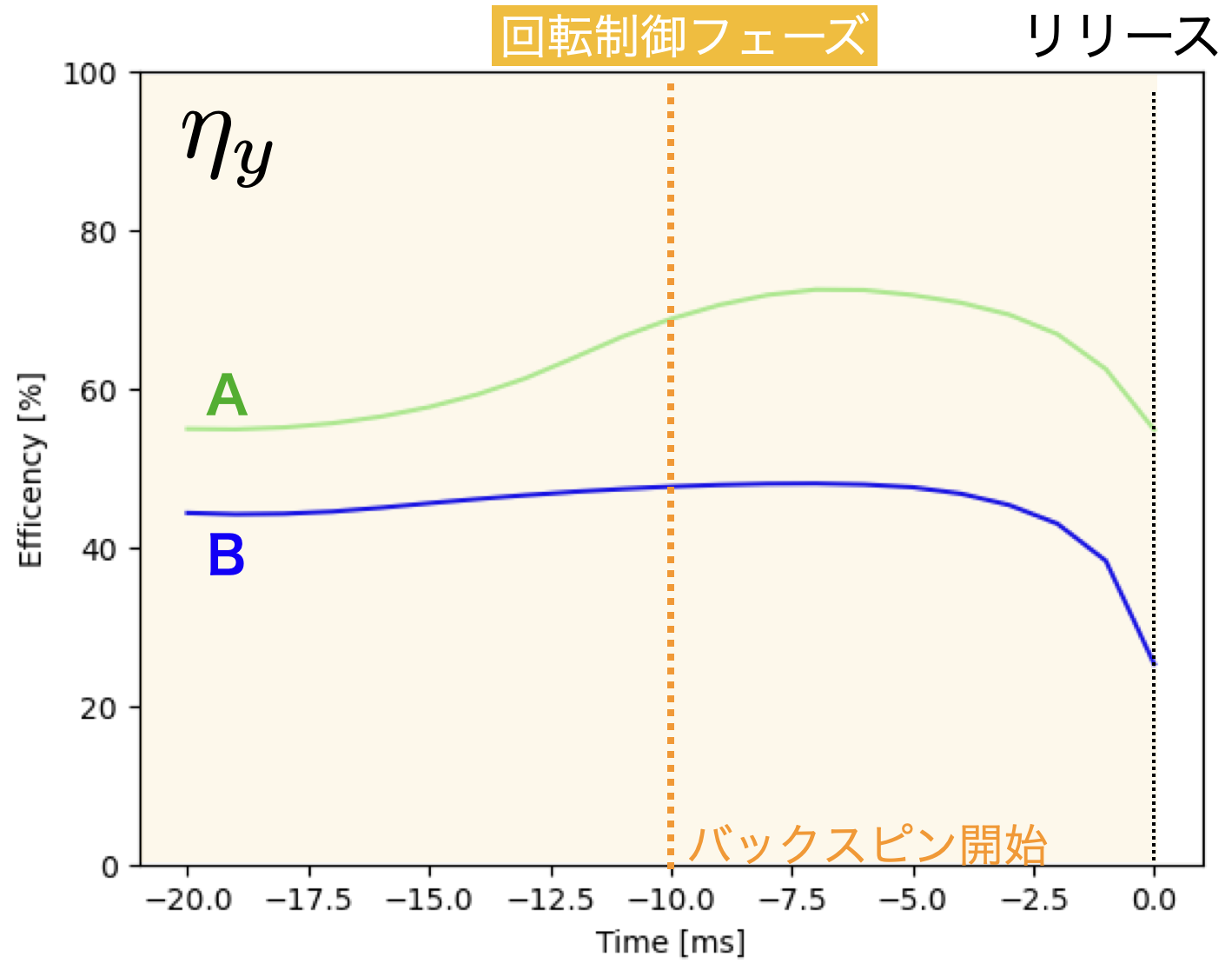
図６：効率ηyの比較

球速（投球方向に作用する力）の効率

前章では，投球の目的として「投球方向に対して正確に大きな速度で投げる」ことを取り上げたが，その目的に対する効率を力発揮の効率を以下のように定義する．

ここで，$\boldsymbol{f}_v$は投球方向に作用する力ベクトルである（図５参照）．

$$
\eta_v = \frac{|\boldsymbol{f}_v|}{|\boldsymbol{f}|}
$$

これは，どれだけ投球方向の力に対してボールに作用する力が寄与するかを示している．ただし，最終的な投球方向に向けた方向と，「回転制御フェーズ」において変化する投球方向の力は少し異なるので注意されたい．

図７は，この効率$\eta_v$をA,Bの投球で比較した．回転制御フェーズにおいてバックスピン回転開始（運動学的回転開始）付近で，Aと比較しBの投球では効率$\eta_v$が高い．

図８には，投球方向に作用する力$|\boldsymbol{f}_v|$の大きさを示す．

図９のtop viewでも比較しているが，図７と同様にバックスピン回転開始付近で，Bの投球方向に作用する力が「一瞬」大きくなる．

Aは平均的に効率良い加速．Bは一瞬の加速

Bの投球はスピン開始時に一瞬大きな力を発揮することで加速するが，Aの投球では回転制御フェーズよりも前のフェーズも含めて，$|\boldsymbol{f}_v|$が小さい．このことから，Aの投球例は平均的に効率良く力を発揮し，Bはバックスピン開始時に一気に加速させる投球と言える．

また，これは身体側の回転で縦振り中心のAと，Bの違いと言える．

図７：効率ηvの比較

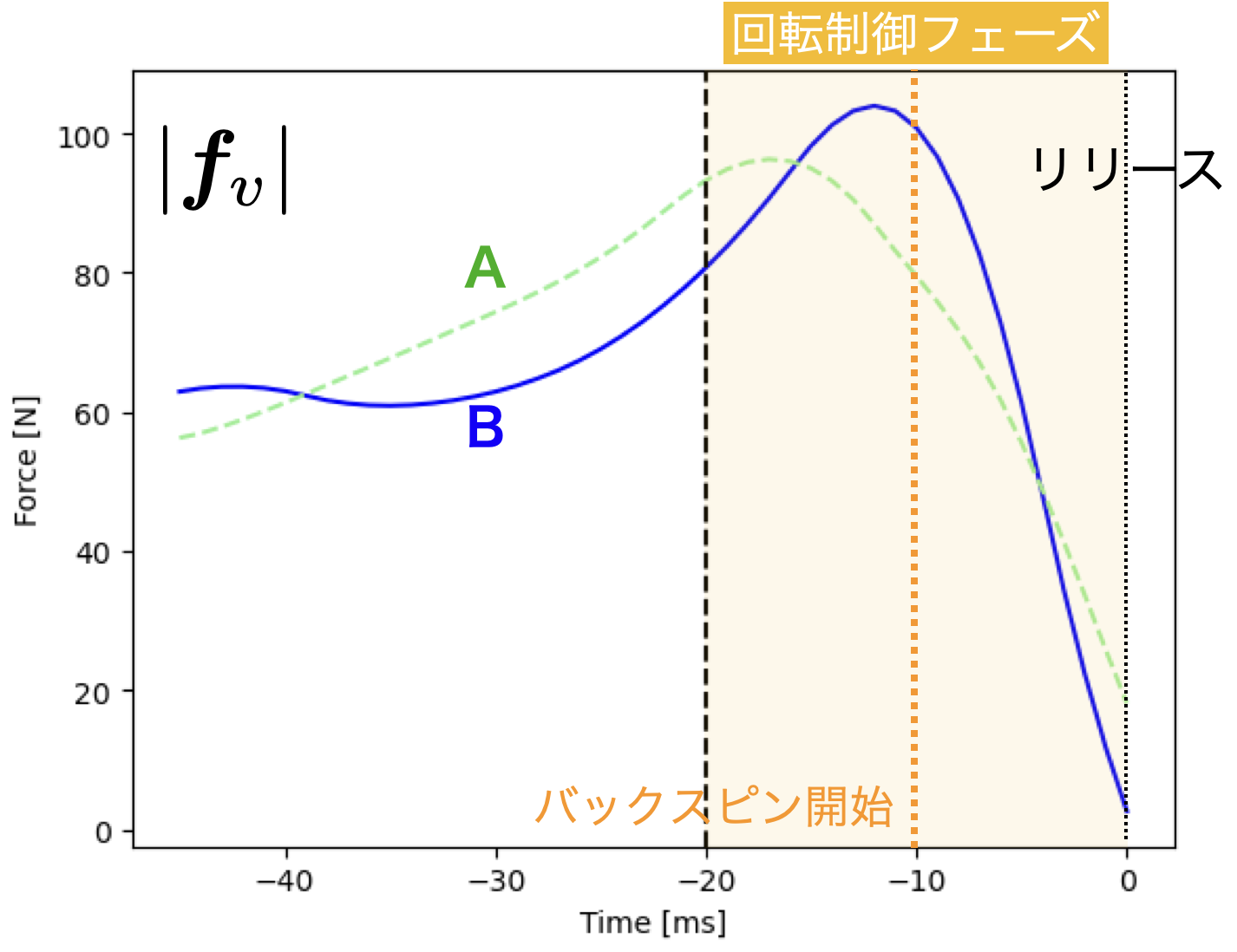
図８：投球方向の力の大きさの比較

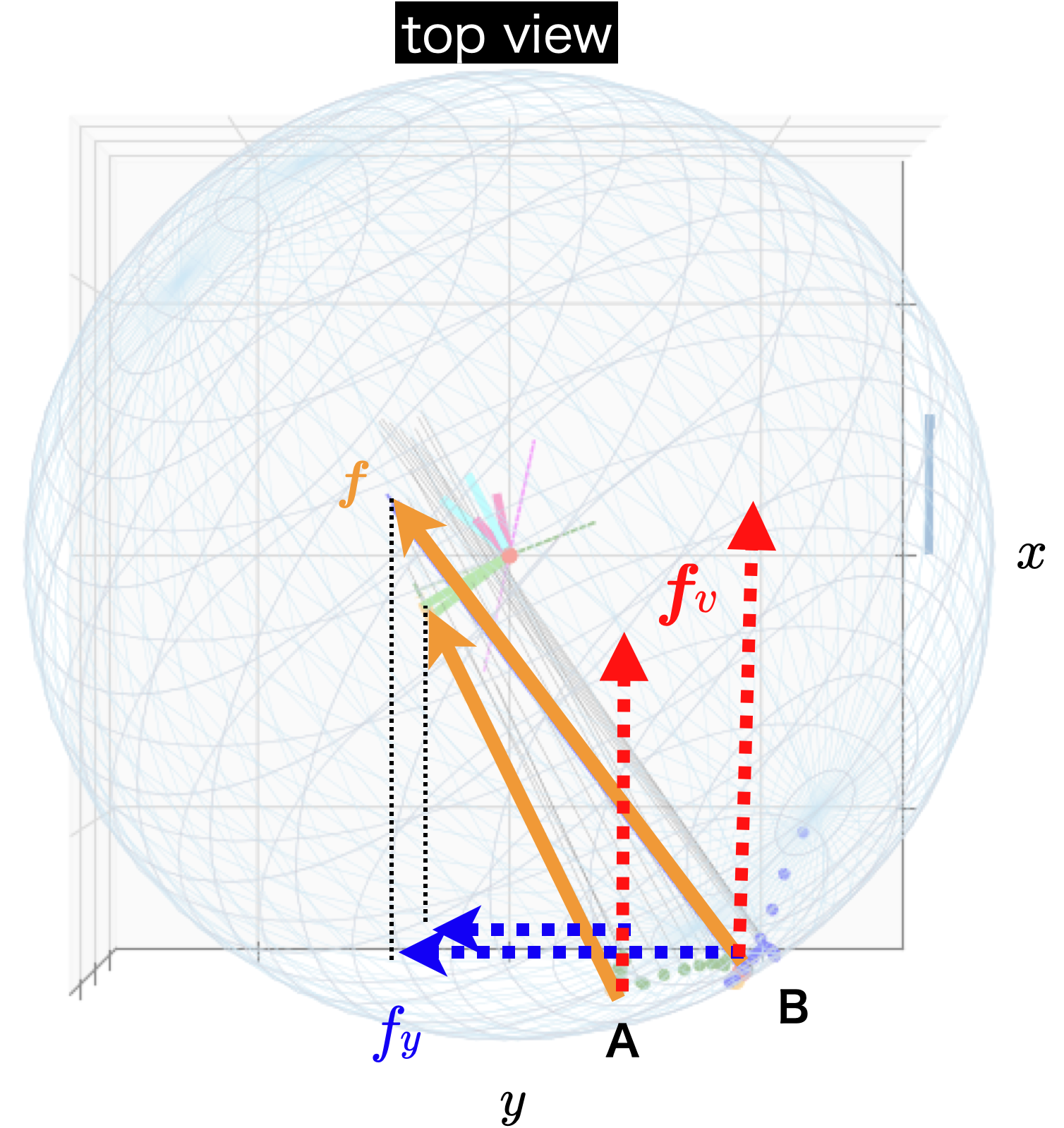
図９：運動学的回転開始（バックスピン開始）時のボールに作用する力の比較（top view）
    Bの投球では，バックスピン開始時に大きな投球方向への力fvと，向心力の水平成分fyが作用する．

まとめ

投球時にボールに対し大きな「向心力」が必ず作用し．向心力の水平方向成分も作用する．つまり，図１の振り子の傾きが大きく，縦振りのスイングに，（そのように呼んでよいかわからないが）横振りの回転（鉛直軸まわりの回転）が加わる．この水平方向成分はストレートの投球においては，あまりうれしくない性質を持つが，これはヒトの都合で致し方ない．しかし，その水平成分を減らすことは，ボールに作用する力の大きさ全体を減らし，かつボールの回転軸を真横にする効果が期待できる．その二つの意味でこの効率も２種類の$\eta_y, \eta_v$を定義した．

また，前章で述べた「縦振り」効果によって，平均的には両方の効率を向上させる効果が期待される．

つまり，スピン軸が真横を向けば，恐らくボールに効率よく所望の力を発揮でき，目的に対して無駄な力発揮が少ない．「縦振り」は力みの少ない（ヒトにとっても効率の良い）投球を実現するかもしれない．

異なる視点から述べると，水平成分$f_y$以外の力成分は，
１：ボールを加速する力
２：ボールを回転する力
　として寄与する．やはり，$f_y$はボールにとっては無駄な力である．

さて，恐らく多くの人の関心は，いったい「どのように縦振りの回転を実現するか？」ということになるだろう．あくまでも推論で検証が必要だが，手先の内旋や回内などだけで解決できる問題ではなく，体幹や下肢からの動力や力の伝達が重要だろうと考えられる．このことは，またどこかで述べることとする．

以下に，動力学的回転開始（バックスピンのトルクが作用し始める）〜運動学的回転開始（バックスピン開始）〜リリースまでの「回転制御フェーズ」における，AとBの投球の比較動画を示す．また，真上（top view），真後（back view），真横（side view）から見た，３種類を示した．

なお，以下の動画で，ボールに作用する力ベクトルがオレンジ色になる時間が，運動学的回転開始（バックスピン開始）のタイミングである．

二つの投球の比較（真上，投球方向：上）

　

二つの投球の比較（真横，投球方向：右） 　 二つの投球の比較（真後，投球方向：前）

おわりに

これまでの一連の記事で，力の作用点や曲率中心を通して，ボールの回転などの制御のメカニズムを明らかにした．これは統計などのようにデータとデータの平均的な関係性ではなく，「力学の幾何学的（ベクトル的）」な解析に基づく可視化によって明らかにしている．

メカニズムを機械学習では明らかにできないとまでは述べないが，バイオメカニクスのメカニズムはこれまで示してきたように，力学の幾何学的な関係から理解されるものがほとんどで，統計やデータサイエンスから理解できるものは少ないだろう．そして，これまでの記事から，力学解析はデータもさることながら，数理から推論できる利点を感じていただけただろうか．

N=1でもかなり説明が可能となる．ここでも，N=2の比較から，さらに多くの知見が得られている．また数理的な理解はその適用できる範囲も明確で，演繹しすぎる危険性も少ないし，数理で生理学モデルなどと合わせて議論することが可能だ．

バイオメカニクスでは幾何学的な解析に基づく数理的理解が重要ということを理解していただけると嬉しい．

1. ストレートではボールの回転によって鉛直上方にボールを持ち上げる力が作用する．これを揚力と呼ぶ．同じ回転数でも回転軸が真横（$y$方向y）を向くほど，最も大きな揚力が得られる．回転数が多い投球ほど，ボールがホップしているように感じるが，実際はボールの軌道が上に変化するのではなく，自由落下の成分を減らしているだけである．
   ↩

2. 回転や空気抵抗を考慮すると実際には複雑で，45度から大きく変化することがある．
   ↩

3. 手とボールは紐を介してつながっている．この時，向心力は手からボールに作用する力．遠心力はボールから手に作用する力．ボール主体で考えると，ボールには向心力が作用する．向心力と遠心力は，大きさが同じで反対向きの力．つまり，作用反作用の力． 遠心力はボール上の座標系から観察した場合に表れる，見かけの力で，外側に引っ張られると感じる（だけ）の力で，実際には作用しない．遠心力は向心力の反作用とした記述は誤りであった．お詫び申し上げる． ↩