Numerical Recipes in Biomechanics #4 ~空間の曲率中心と力学~

Last updated at 2025-10-08Posted at 2025-09-04

はじめに

曲率中心については過去にまとめた記事

もご覧になっていただければと思う．

実際の点の空間運動を計測し，その曲率（軌道の曲がり具合）やその逆数である曲率半径の計算した例は散見されるが，空間の曲率中心を計算した例はほとんどない．しかし，曲率を内在する，空間における「曲率中心の位置」の方がむしろバイオメカニクスで重要な意味を持つ．

ここでは，曲率と力学の数理関係をまとめ，実際に曲率中心を計算する方法を述べる．

なお，あらかじめ重要なことを述べておくと，この記事の中で式は多く，ベクトルの外積の計算を多用している．外積はPythonのnumpy.cross()関数を利用すれば計算は簡単だし，実際の数値計算では外積を用いずに引き算で置き換えることもできるということを，この記事で理解していただけると幸いだ．

曲率中心と力学

バイオメカニクスなどの研究で，空間における運動軌道の曲率中心（center of curvature）を計算することは，あまり多くないかもしれない．曲率半径も重要だが，空間における軌道からみたその方向や位置も，物理的に大きな意味を持つ．また，これは単なる運動学・幾何学パラメ―タではなく，質点力学を記述する力学パラメータでもある．なぜならそれは速度と加速度で計算されるため，それはダイナミクスそのものである．曲率中心の数学的記述では，力学との関連に言及した記述は教科書や研究であまりないので，参考にしていただければと思う．

曲率中心は多関節運動の代表点

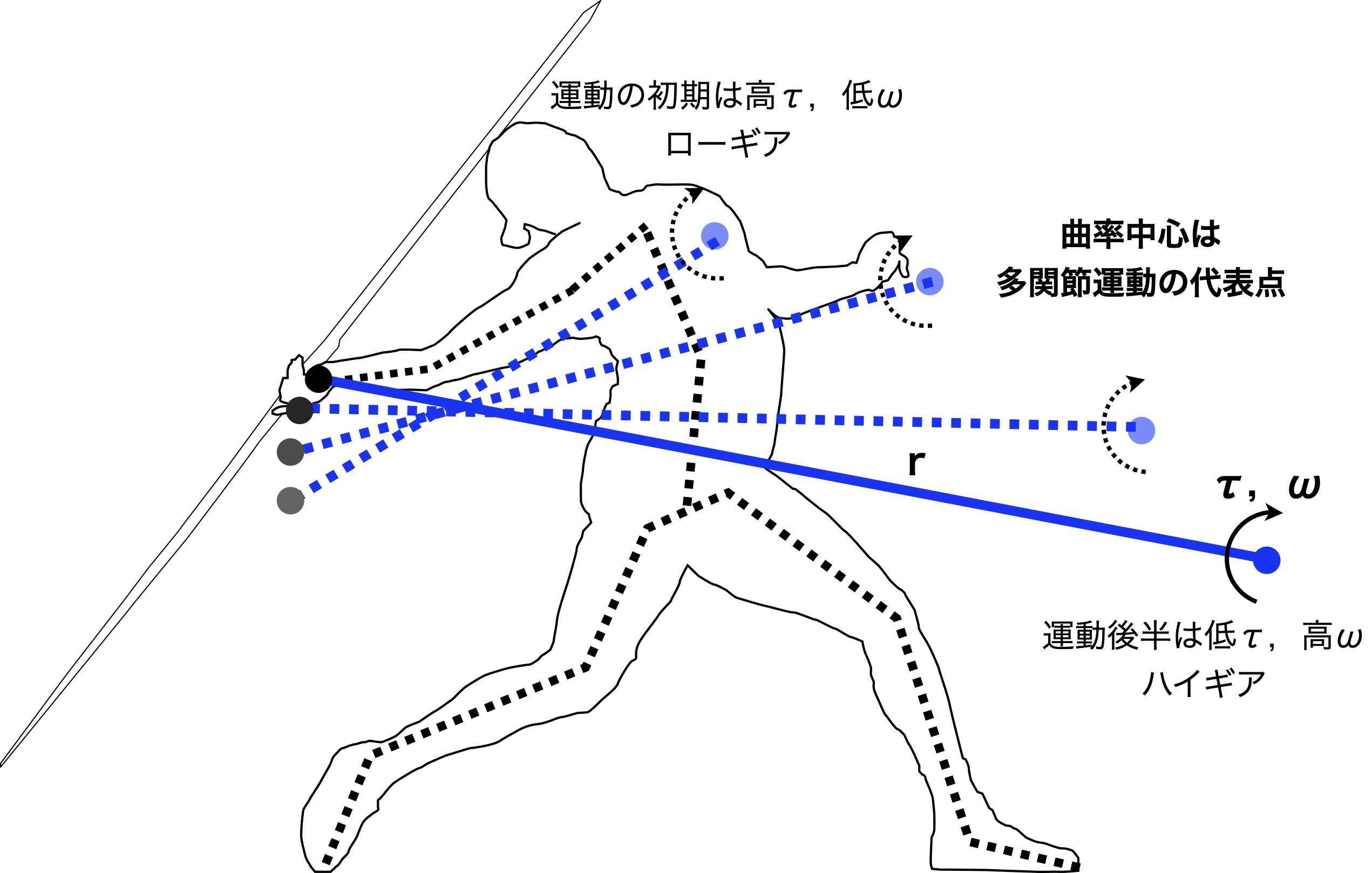
図１：（図はイメージ）身体を一つの振り子とみなせば，曲率半径はギア比の目安で，
　　  曲率中心は空間でギヤチェンジの様子を可視化する．

身体運動では，多関節運動を一つの質点の運動として（代表点として）捉えることで，物事が見えやすくなる．

例えば，ボールの運動の曲率中心は身体の「多関節運動の代表点」と捉えればよく，投擲物体や手などの末端の運動の曲率中心の位置は，全身運動の力学を一つの位置に反映している．リリース直前のように力が作用しなくなるときを除けば，曲率中心の方向は回転を与える向きを反映する．投擲物を斜めに回転させようてしているのか，縦に回転させようとしているのかなどが見えてくる．

また，投擲運動やスイング運動における曲率半径はリリースやインパクトに向けて次第に大きくなる．これは自動車や自転車のギアチェンジと同じ原理で，筋肉（モータでも同様）のアクチュエータの性質から，加速するにつれ半径を大きくしないとアクチュエータの動力を効率よく伝達できなため，半径が大きくなるのは身体の自然なふるまいである．特に曲率半径はギアの梃子の長さ（振り子の長さ）を意味し，長さの変化はギア比の変化に相当し，トルク$\boldsymbol{\tau}$と角速度$\boldsymbol{\omega}$の状態に応じ，機械的インピーダンス・マッチングを行っているかを判定する指標になるだろう．

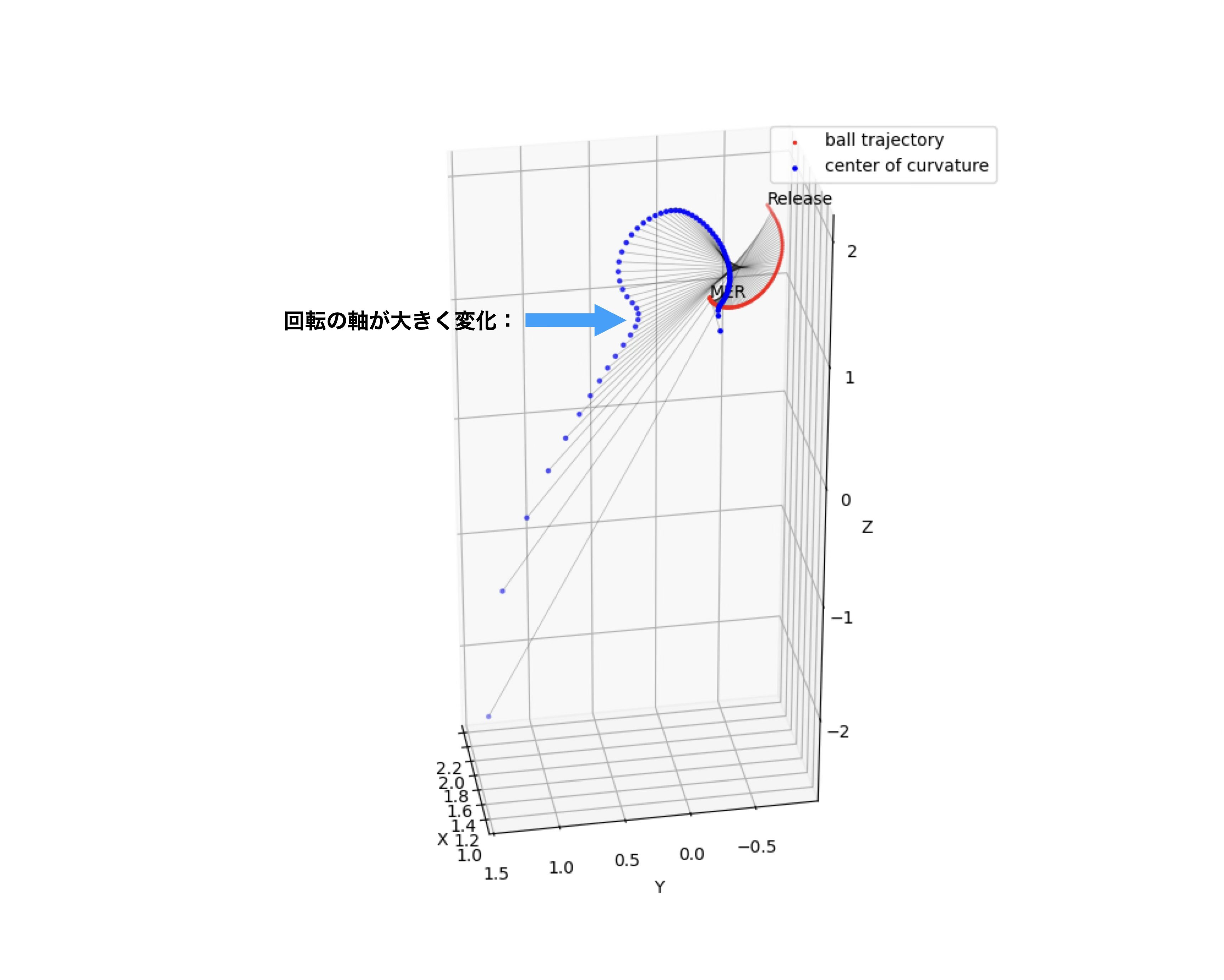
図２：曲率中心とその移動の変曲点

図２はボールの軌道（赤）と，それに対応する曲率中心（青）を示しているが，その曲率中心の移動の向きなどが大きくくり変わる変曲点（矢印あたり）は，回転の軸が大きく変化している点で，ギアチェンジや，身体側の負荷が大きくなる目安となるだろう．少なくとも滑らかに円運動のように変化している曲率中心の運動が突如向きを変えるのだから，物理的に何かがおきていることは間違いない．

この可視化により，投手の投げ方も，ランニングのようにピッチ投法（曲率半径が小），ストライド投法（曲率半径が大）のような分類も可能かもしれない．検証していないが，西武の今井投手の投げ方はピッチ投法で，ドジャーズの大谷投手はストライド投法ではないかと想像している．あくまでもイメージを伝えるためで，これは想像の範囲を超えないので，ご容赦いただきたい．しかし，ピッチ投法かストライド投法の区別を曲率による数理で示すことができるだろう．

曲率中心の計算の数値計算の不安定性

空間で曲率中心を計算したとしても，その計算は近似が多い¹．一方，曲率計算を計算するフレネ・セレの公式（the Frenet–Serret formulas）²（例えば，文献１，２）をそのまま用いて，厳密に，曲率中心を計算しようと思うと，いくつか困難が待ち受けている．この記事で記述した式を使えば，比較的安定して曲率の計算ができるだろう．ここではPythonコード付きで示していきたい．

まずは曲率中心を計算する意義を改めて述べ，その時の計算にまつわる実際について述べていく．どこまでその意義が伝わるかわからないが，過去の記事を復習しながら話を進めていく．

そもそも曲率中心とは

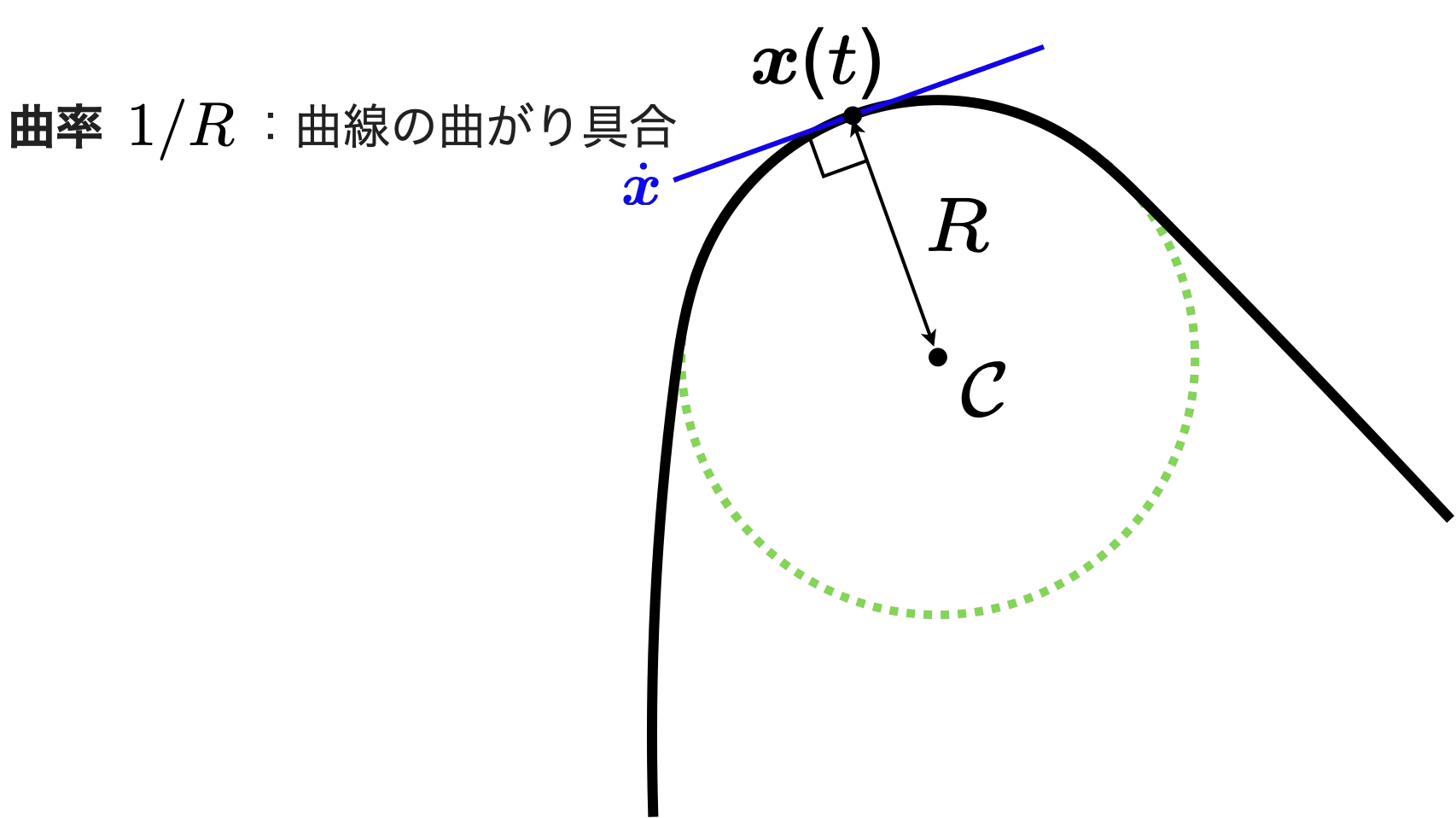
図３：曲率とは局所的な曲がり具合の円への近似

物体（質点）の曲線運動において，局所的な（つまり，図３の曲線軌道$\boldsymbol{x}$が接している点における）曲がり具合を半径$R$の円に近似し，その「曲線の曲がり具合」を$\frac{1}{R}$で表し，それを曲率（curvature）と呼び，その「回転の中心」$C$を曲率中心（center of curvature）と呼ぶ．

曲率中心は，力学と無縁で，幾何学的なパラメータと考えてしまうかもしれない．たしかに微分幾何学の教科書で，特に平面的な曲率は，線分幾何学的な説明が中心で，わかりやすく述べると回転の中心である．質量と無関係で幾何学的に定まる．

しかし，物体の運動を曲げるには力が必要なので，曲率中心は力学と密接に関係する．力学との関連ではKIT物理ナビゲーション

も参照するとよいだろう．

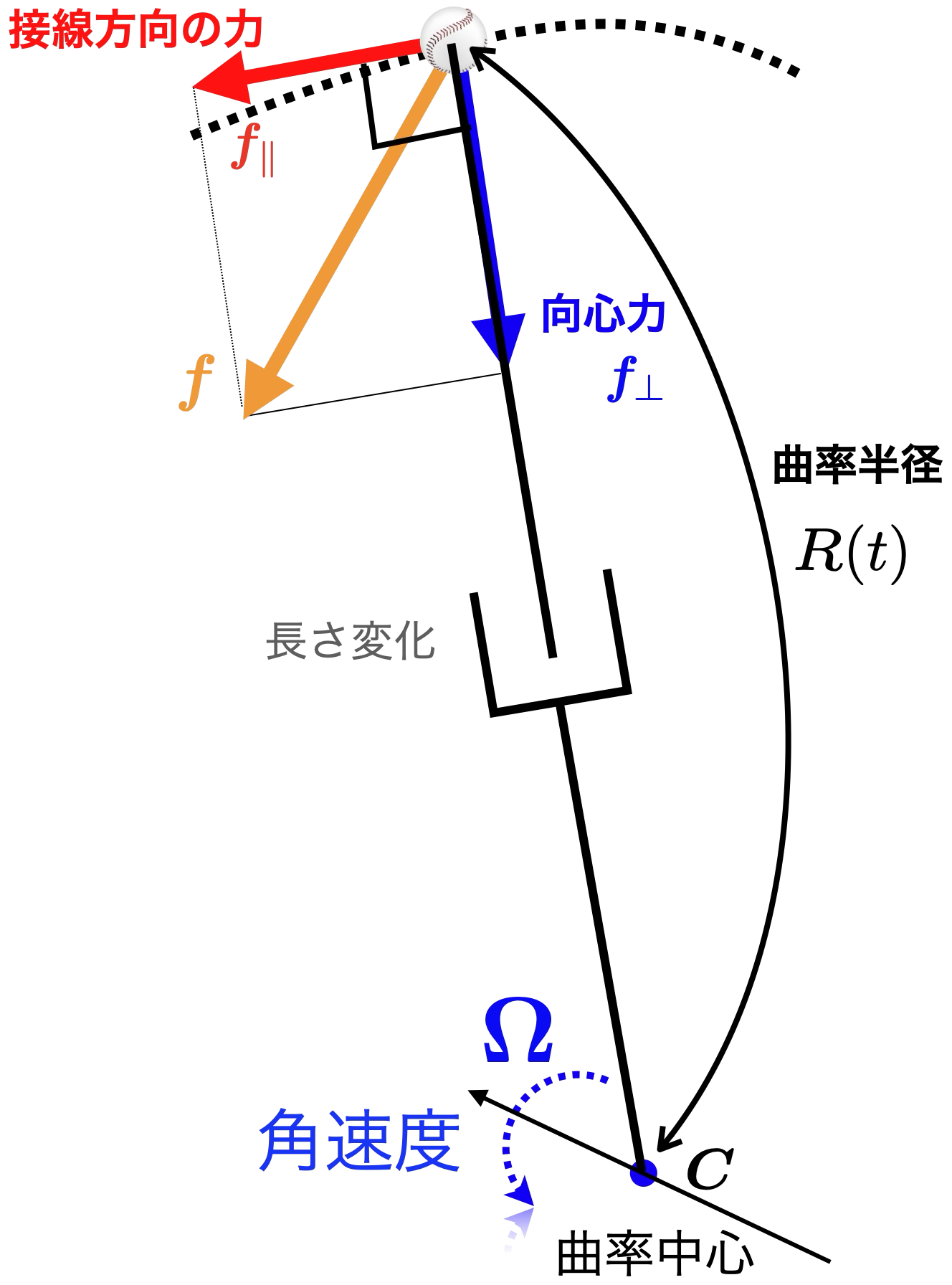
図４：可変長振子：ボールの空間軌道と曲率中心とその力学

図４に示しているように，たとえばボールの軌道を曲げるのためには，ボールに対して力$\pmb{f}$が作用するが，曲率中心を原点とする極座標を考えれば，それは直交する２つの力に分配される．ひとつは接線方向に作用するボールの加速に寄与する力で，もう一つ曲率中心方向に作用する向心力（centripetal force）である．それ以外にボールには重力も作用する³が，基本的にはこの物理的意味が明確な２つの力で議論すればよい⁴．

前の記事「ベクトル三重積とベクトルの成分分解」で，ベクトルをある方向の成分と，それに直交する方向の成分に分解する方法を述べたが，ボールに作用する力$\boldsymbol{f}$や加速度を，接線方向成分$f_{\parallel}$とそれに対して直交する成分$f_{\perp}$とに分解すると，直交する成分$f_{\perp}$はその向心力に相当する．

注意：式の表示におけるQiitaの不具合について⁵

このボールの運動は，長さ$R(t)$が変化し質量を無視できる糸で，曲率中心$C$からつながった振り子と考え，ここではこれを可変長振子（variable length pendulum）と呼ぶこととする⁶．

ここで一つ注意していただきたいことは，向心力は回転を維持するための力で，回転運動中に糸を切ると，ボールは接線方向に飛んでいってしまう．このことからも，向心力はボールに作用するが，あくまでも「向心力は回転を維持するための力」であるということに留意していただきたい．

向心力の計算はKIT物理ナビゲーションにも詳しく書かれているが，ここでは前の記事を利用し，向心力や曲率中心の計算方法を詳しく述べる．

曲率中心の数理

曲率中心の数理は

も参照していただきたい．また最後に式をまとめたので参照されたい．

下記の内容は数理的な展開が多いが，基本的にはベクトルの内積（dot product）と外積（cross product, outer product）を利用した計算だけで構成され，難しい数学は含んでいない．多くは幾何学的意味から意図は理解できるはずだし，幾何学的な理解が不可欠である．ここで示すように，力学はどちらかというと微分よりも，ベクトルをベースとした幾何学的な数理の理解が重要である．曲率だけでなく，力学を理解するには，まずは内積と外積の幾何学的意味を，数理とともにしっかり理解することだ．

なお，ここで多用する内積は２つのベクトル間の射影を表し，外積は直交する方向のベクトルを形成するが，詳細は「note記事」をご覧になっていただければと思う．

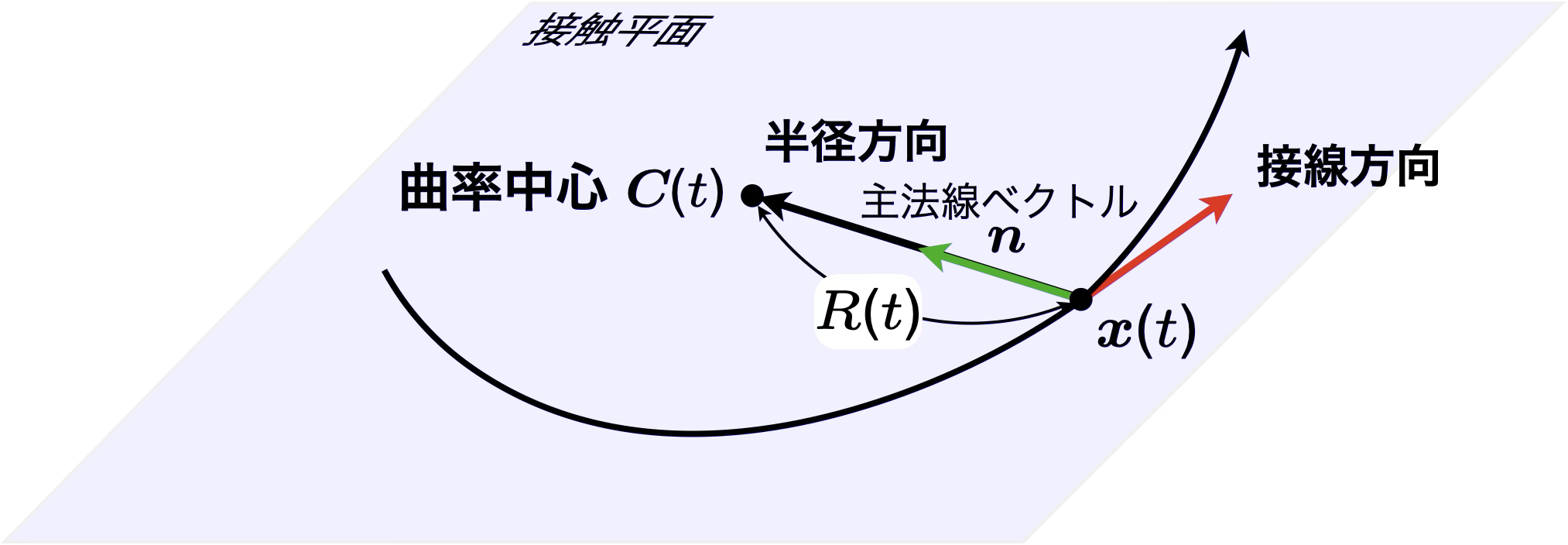
図５：曲率中心

物体の軌道を$\boldsymbol{x}(t)$とすると，$\boldsymbol{x}(t)$の曲率中心$\boldsymbol{C}(t)$は，

$$
\begin{aligned}
\boldsymbol{C}(t) &= \boldsymbol{x}(t) + R(t) \boldsymbol{n}(t)
\\
&= \boldsymbol{x}(t) + \frac{1}{\kappa(t)}\boldsymbol{n}(t)
\end{aligned}
$$

のように，曲率中心は$\boldsymbol{x}(t)$からみて，$\frac{1}{\kappa} \boldsymbol{n} = R \boldsymbol{n}$の位置にあると定義されている．
ここで，$\boldsymbol{n}(t)$は，速度$\dot{\pmb{x}}$と加速度$\ddot{\pmb{x}}$によって張られる平面内で，軌道$\pmb{x}$の接線方向$\dot{\pmb{x}}$に直交する方向を向く単位主法線ベクトル（unit principal normal vector）である．これは物体の位置$\boldsymbol{x}$から見た，曲率中心方向の単位ベクトルである．また，曲率半径を$R(t)$とすると，曲率$\kappa(t)$とは$R(t)$の逆数

$$
\kappa(t) = \frac{1}{R(t)}
$$
によって，曲線の曲がり具合を示す．

単位主法線ベクトル

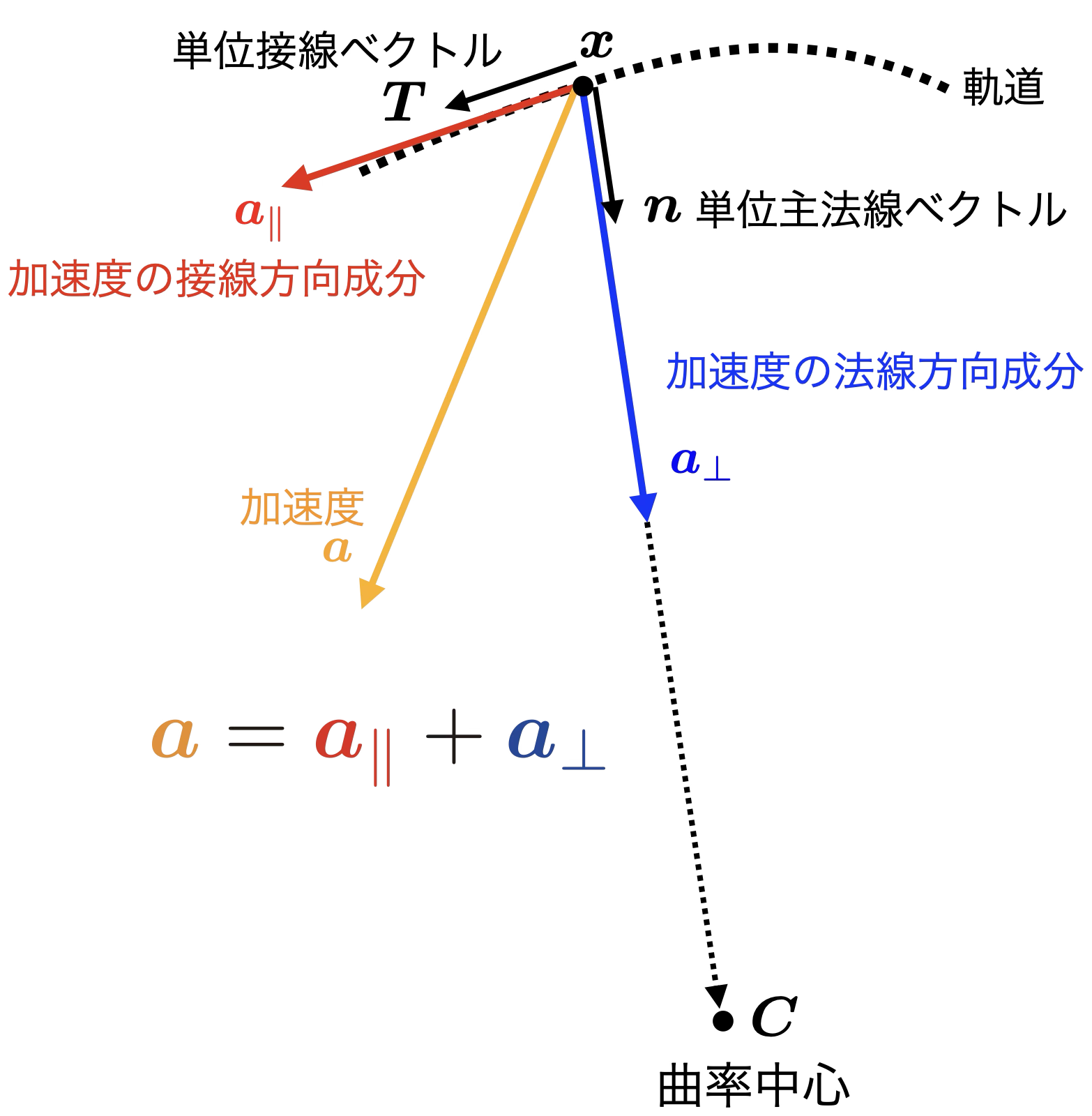
図６：単位主法線ベクトル

曲率中心$\pmb{C}$の位置は$\pmb{x}$からみて，単位主法線ベクトル$\pmb{n}$方向を向く．ここで，軌道$\boldsymbol{x}(t)$の速度$\boldsymbol{v}$と加速度$\boldsymbol{a}$を，$\boldsymbol{v} = \dot{\boldsymbol{x}},~ \boldsymbol{a} = \ddot{\boldsymbol{x}}$とし，前の記事「ベクトル三重積とベクトルの成分分解」を思い出すと，単位主法線ベクトル$\pmb{n}$は，速度$\pmb{v}$と加速度$\pmb{a}$によって張られる平面内で，軌道$\pmb{x}$の接線方向$\pmb{v}$に直交する方向なので，速度ベクトルの単位ベクトルを

$$\pmb{T} = \frac{\dot{\pmb{x}}}{|\dot{\pmb{x}}|}=\frac{\pmb{v}}{|\pmb{v}|}$$

とすると，これは接線方向の加速度$\pmb{a}_{\parallel}$単位ベクトルでもあるので，

$$
a_{\parallel} = |a_{\parallel}|\pmb{T} = (\pmb{T}^T \pmb{a}) \pmb{T}
$$

となることから，前の記事の射影$a_{\parallel}$と反射影$a_{\perp}$を利用することで，つまり，加速度$\pmb{a}$から接線方向の加速度$\pmb{a}_{\parallel}$を引き算するだけで，向心力方向（単位主法線方向）の加速度

$$
\begin{aligned}
a_{\perp} &= \pmb{a} - a_{\parallel}
\\
&= \pmb{a} - (\pmb{T}^T \pmb{a}) \pmb{T}
\\
&= \pmb{T} \times (\pmb{a} \times \pmb{T})
\\
&=\frac{\pmb{v}}{|\pmb{v}|} \times (\pmb{a} \times \frac{\pmb{v}}{|\pmb{v}|})
\\
&= \frac{\pmb{v} \times (\pmb{a} \times \pmb{v})}{|\pmb{v}|^2}
\end{aligned}
$$

を得ることができ，つまり，上式のようにベクトル三重積を計算せずに$a_{\perp}$を計算できる．また，単位主法線ベクトル$\pmb{n}$は$a_{\perp}$の単位ベクトルなので，分母の大きさ$|\pmb{v}|^2$は関係なく，$\pmb{v} \times (\pmb{a} \times \pmb{v})$の大きさを計算すればよいので，

$$
\boldsymbol{n} = |a_{\perp}| = |\pmb{a} - a_{\parallel}| = \frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})|} = \frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{v}| ~|\boldsymbol{a} \times \boldsymbol{v}|}
$$
となる⁷．

曲率

接線単位ベクトル$\pmb{T} = \pmb{v}/|\pmb{v}|$とするとき，弧長パラメータ$s$を用いた曲率$\kappa$の定義⁸

$$
\kappa = \left|\frac{d\pmb{T}}{ds}\right| = \left|\frac{1}{ds/dt}\frac{d\pmb{T}}{dt}\right| = \frac{1}{|\pmb{v}|} \left|\frac{d\pmb{T}}{dt}\right|
$$

から，曲率は

$$
\kappa = \frac{|\boldsymbol{a} \times \boldsymbol{v}|}{|\boldsymbol{v}|^3}
$$
より計算できる．note記事「曲率の力学」なども参照されたい．

曲率中心

以上から
$$
\begin{aligned}
\frac{1}{\kappa}\boldsymbol{n} &=
\frac{|\boldsymbol{v}|^3}{|\boldsymbol{a} \times \boldsymbol{v}|} \frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{v}| ~|\boldsymbol{a} \times \boldsymbol{v}|}
\\
&= |\boldsymbol{v}|^2 ~\frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{a} \times \boldsymbol{v}|^2}
\end{aligned}
$$
を得て，曲率中心は

$$
\begin{aligned}
\boldsymbol{C}(t) &= \boldsymbol{x}(t) + \frac{1}{\kappa(t)}\boldsymbol{n}(t)
\\
&= \boldsymbol{x}(t) +
|\boldsymbol{v}|^2 ~\frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{a} \times \boldsymbol{v}|^2}
\end{aligned}
$$

より計算できる．ここまで展開することで，数値計算上のムダがかなり省かれ，曲率中心の数値計算精度も向上する．

空間における曲率の力学

質量$m$の質点が運動する際の，質点の速度を$\pmb{v}$，加速度を$\pmb{a}$，接線方向の単位ベクトルを$\pmb{T}=\pmb{v}/|\pmb{v}|$，それに直交する半径方向の単位主法線ベクトルを$\pmb{n}$とすると，質点の加速度$\pmb{a}$は，前の記事での述べたように，接線方向$\pmb{T}$の加速度$a_{\parallel}$と，半径方向の加速度$a_{\perp}$に分解でき，
$$
\begin{aligned}
\pmb{a} &= a_{\parallel} + a_{\perp}
\\
&= |a_{\parallel}|\pmb{T} + |a_{\perp}|\pmb{n}
\end{aligned}
$$
と書ける．

接線方向

接線方向（$\pmb{T}$方向）の加速度の大きさ（ノルム）$| a_{\parallel} |$は，加速度ベクトル$\pmb{a}$と接線方向の単位ベクトル$\pmb{T}$との内積$\boldsymbol{a}^T \boldsymbol{T}$で，または，前章でも述べたが，速度ベクトルの大きさ$|\boldsymbol{v}|$の時間微分で定まるので，接線方向の加速度は，それらと接線方向の単位ベクトル$\pmb{T}$との積で

と書くことができる．このため，接線方向に作用する力$\pmb{f}_{\parallel}$は，

$$
\pmb{f}_{\parallel} = m (\boldsymbol{a}^T \boldsymbol{T})\boldsymbol{T} = m \frac{d}{dt}|\boldsymbol{v}| \boldsymbol{T}
$$
となる（補足１）．また，曲率中心まわりの角速度ベクトルを$\pmb{\Omega}$，曲率中心からみた質点の位置ベクトルを$\pmb{r}=-R \pmb{n}$とすると，回転の力学から，

$$
\pmb{f}_{\parallel} = m \dot{\pmb{\Omega}}\times \pmb{r} + 2m \pmb{\Omega}\times \dot{\pmb{r}}
$$

と書くこともできる．ここで，右辺第１項はオイラー力（Euler force，角加速力），第２項はコリオリ力（Coriolis force）と呼ばれる．オイラー力は振り子の回転の力（角加速度による力）で，コリオリ力は回転している振り子の長さが変化することで，接線方向に作用する力である．これらの回転の力学については「Sports Biomechanics Geek #7　〜多関節運動の代表値　曲率の力学〜」なども参照されたい．

ここで，角速度ベクトル$\pmb{\Omega}$は半径方向$\pmb{n}$まわりの角速度は0で，速度ベクトル$\pmb{v}$と加速度ベクトル$\pmb{a}$で張られる平面の法線方向$\pmb{v} \times \pmb{a}$を向くベクトルであることにも注意が必要である．

半径方向（軌道の法線方向）

質点はその位置における曲率円の円周上を運動しているとみなすことができ，質点にはその曲率中心に向かう向心加速度$a_{\perp}$が作用する．この向心加速度$a_{\perp}$は，この記事の前半より，加速度$\pmb{a}$から，接線方向の$a_{\parallel}$を引くことで，

$$
a_{\perp} = \pmb{a} - a_{\parallel} = \frac{\pmb{v} \times (\pmb{a} \times \pmb{v})}{|\pmb{v}|^2}
$$

を得て，その大きさは，

$$
|a_{\perp}| = |\pmb{a} - a_{\parallel}| = \frac{|\pmb{v}| |\pmb{a} \times \pmb{v}|}{|\pmb{v}|^2} = \frac{|\pmb{a} \times \pmb{v}|}{|\pmb{v}|}
$$

となる．一般に，質点が曲線軌道上を運動している場合，各瞬間の曲率半径の円周上を質点が運動しているとみなすことができ，質点に作用する向心力は

$$
f_{\perp} = \frac{m}{|\pmb{v}|^2} \pmb{v} \times (\pmb{a} \times \pmb{v})
$$

となる．先程と同様に，曲率中心まわりの角速度ベクトルを$\pmb{\Omega}$，曲率中心からみた質点の位置ベクトルを$\pmb{r}=-R \pmb{n}$とすると，回転運動の力学から向心加速度は，

$$
a_{\perp} = \pmb{\Omega} \times (\pmb{\Omega} \times \pmb{r})
$$

なので，向心力$\pmb{f}_{\perp}$は，回転の力学と，これまで議論してきた幾何学的理解から

$$
\begin{aligned}
f_{\perp} &= m \pmb{\Omega} \times (\pmb{\Omega} \times \pmb{r})
= -m |r| |\pmb{\Omega}|^2 \pmb{n}
\\
&= m|a_{\perp}| \pmb{n} = m (\pmb{a}^T \pmb{n}) \pmb{n}
\\
&= m \pmb{a} - f_{\parallel}
\end{aligned}
$$
と書くことができる．また，その大きさは

$$
\begin{aligned}
|f_{\perp}| &= \frac{m |\pmb{v}|^2}{R}
\\
&= m |a_{\perp}| = m \frac{|\pmb{a} \times \pmb{v}|}{|\pmb{v}|}
\end{aligned}
$$

となる．

なお，繰り返しになるが，角速度ベクトル$\pmb{\Omega}$は，速度ベクトル$\pmb{v}$と加速度ベクトル$\pmb{a}$で張られる平面の法線方向$\pmb{v} \times \pmb{a}$を向くベクトルで，その大きさは

$$
\begin{aligned}
|r| |\pmb{\Omega}|^2 = |a_{\perp}| = \pmb{a}^T \pmb{n} = \frac{|\pmb{a} \times \pmb{v}|}{|\pmb{v}|}
\end{aligned}
$$

となるので，

$$
|\pmb{\Omega}| = \sqrt{\frac{|a_{\perp}|}{|\pmb{r}|}} = \sqrt{\frac{\pmb{a}^T \pmb{n}}{|\pmb{r}|}} = \sqrt{\frac{|\pmb{a} \times \pmb{v}|}{|\pmb{v}||\pmb{r}|}}
$$

角速度ベクトル$\pmb{\Omega}$も

$$
\pmb{\Omega} = |\pmb{\Omega}| \frac{\pmb{v} \times \pmb{a}}{|\pmb{v} \times \pmb{a}|}
$$

のように計算できる．

曲率とその力学に関係する式のまとめ

曲率

$$
\kappa = \frac{1}{R} = \frac{|\boldsymbol{a} \times \boldsymbol{v}|}{|\boldsymbol{v}|^3}
$$

単位主法線ベクトル

$$
\boldsymbol{n} = \frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{v}| ~|\boldsymbol{a} \times \boldsymbol{v}|}
$$

接線方向の加速度

主法線方向（半径）の加速度

$$
\begin{aligned}
a_{\perp} &= \pmb{a} - a_{\parallel}
\\
&= \frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{v}|^2}
\end{aligned}
$$

曲率中心

$$
\begin{aligned}
\boldsymbol{C}(t) &= \boldsymbol{x}(t) + \frac{1}{\kappa(t)}\boldsymbol{n}(t) = \boldsymbol{x}(t) + R(t) \boldsymbol{n}(t) = R(t) a_{\perp}
\\
&= \boldsymbol{x}(t) +
|\boldsymbol{v}|^2 ~\frac{\boldsymbol{v} \times (\boldsymbol{a} \times \boldsymbol{v})}{|\boldsymbol{a} \times \boldsymbol{v}|^2}
\\
&= \boldsymbol{x}(t) + \frac{|\boldsymbol{v}|^3}{|\boldsymbol{a} \times \boldsymbol{v}|}
\left(\frac{\pmb{a} - a_{\parallel}}{|\pmb{a} - a_{\parallel}|} \right)= \boldsymbol{x}(t) + \frac{|\boldsymbol{v}|^3}{|\boldsymbol{a} \times \boldsymbol{v}|}
\frac{\pmb{a} - (\boldsymbol{a}^T \boldsymbol{T})\boldsymbol{T}}{|\pmb{a} - (\boldsymbol{a}^T \boldsymbol{T})\boldsymbol{T}|}
\end{aligned}
$$

実際に曲率中心の位置（曲率ベクトル）$\pmb{C}$をPythonで計算する場合，上から２行目でも，３行目で計算しても，数値精度はほぼ同等である．アルゴリズムの組みやすい方法を選択するとよいだろう．以下のコードでは３行目を使用した．

Python コード

実際に約140km/hの投球時のモーションキャプチャ（1kHz）で計測したボールの重心の位置データを利用し，曲率計算を計算する．データは最大外旋位（MER）からリリース後10フレーム（10ms）までの，ボールの空間軌道データを下記にアップした．おおよそ$X$の正の方向へ飛翔する投球である．

もし，ご興味のある方は，下記のコードを実行すると，コードの後に示した「ボールの速度のグラフ」（図７）と，「ボールと曲率中心の３D軌道のグラフ」（図８）を，このコードで描画できる．下記のリンクからコードとデータをダウンロードしていただきたい．

コードとデータのディレクトリ構造

以下のgithubに，下記のPythonコードとサンプルデータをおいているので，そちらからダウンロード可能である．

サンプルデータとコードはこちらから → GitHub: curvature

また，データの置き場所は，下記のように変更した．

curvature/
├── data/
│　　　└── ball_trajectory.csv ← サンプルデータ
└── code/
　　　└── curvaturee.py ← Pythonコード

codeディレクトリ下にPythonコードcurvature.pyを配置し，dataディレクトリ下にサンプルデータのball_trajectory.csvを置いた．

このコードをそのまま実行する場合，dataとcodeのディレクトリ構造を維持していただきたい．もちろん，慣れている方は自由に設定していただければと思う．

################################
# データディレクトリ
################################
script_dir = os.path.dirname(os.path.abspath(__file__))
data_dir = os.path.join(script_dir, '../data', 'ball_trajectory.csv')
data = pd.read_csv(data_dir, header=0).values

この変更に応じ，Pythonコードcurvature.pyのディレクトリをos.path.dirname()で設定し，そこからdataディレクトリに移動し，サンプルデータのball_trajectory.csvを読み込むように変更した．

コードの補足

以下のコードで，ボールの速度のグラフと，ボールの軌道と曲率中心の3Dグラフを描けるだろう．

なお，軌道$\pmb{x}$から速度，加速度$\pmb{v}, \pmb{a}$を時間微分で計算をするために，平滑化スプライン（smoothing spline）を用いている．これについては記事「Numerical Recipes in Biomechanics #2 ~平滑化スプラインのpythonコードを更新~」をご参照いただければと思う．

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import UnivariateSpline
import os

################################
# データディレクトリ
################################
script_dir = os.path.dirname(os.path.abspath(__file__))
data_dir = os.path.join(script_dir, '../data', 'ball_trajectory.csv')
data = pd.read_csv(data_dir, header=0).values

################################
# Parameters
################################
weight_v = .00007 # 速度用のフィルタ重み係数
weight_a = .00009 # 加速度用のフィルタ重み係数
sf = 1000. # サンプリング周波数

################################
# Math Functions
################################
# ノルム（大きさ）
def norm(vec_array):
    if vec_array.ndim == 1:
        return np.linalg.norm(vec_array)
    else:
        return np.linalg.norm(vec_array, axis=1)

# 単位ベクトル
def unit_vec(data_vec):
    if data_vec.ndim == 1:
        data_norm = np.linalg.norm(data_vec)
    else:
        data_norm = np.linalg.norm(data_vec, axis=1)[:,np.newaxis]
    return data_vec/data_norm

# 内積
def dot_product(a, b):
    if a.ndim == 1 and b.ndim == 1:
        return np.sum(a * b)
    elif a.ndim == 2 and b.ndim == 2:
        return np.sum(a * b, axis=1)

# 外積
def cross_product(a, b):
    if a.ndim == 1 and b.ndim == 1:
        return np.cross(a, b)
    elif a.ndim == 2 and b.ndim == 2:
        return np.cross(a, b, axis=1)

################################
# Smoothing Spline
################################
# スプライン平滑化：データの微分に利用
def smoothing_spline(data, weights=1.0, sf=1000.0, order=0, degree=4):

    """
    UnivariateSplineを用いて時系列データを平滑化（および微分）する。

    Parameters
    ----------
    data : array-like
        平滑化したい時系列データ。1次元または2次元配列
    weights : float or array-like 
        平滑化の重み。スカラーまたは配列．配列の場合データの列数とし，各列ごとに個別に重みを与えることができる
    sf : float
        サンプリング周波数（Hz）
    order : int, optional
        微分の次数（0なら平滑化のみ）。デフォルトは0
    degree : int, optional
        スプラインの次数。デフォルトは4．加速度まで計算する場合はデフォルトの4とする．

    Returns
    -------
    smoothed : ndarray
        平滑化（または微分）されたデータ
    """

    data = np.asarray(data)
    if data.ndim == 1:
        data = data[:, None]
    
    # weightがスカラーまたはデータの列数と一致する配列であることを確認
    if not np.isscalar(weights):
        assert len(weights) == data.shape[1], f"weights must be scalar or array of length {data.shape[1]}, but got length {len(weights)}"
    
    # data = np.asarray(data)
    if data.ndim == 1:
        data = data[:, None]

    n_samples, n_series = data.shape
    t = np.arange(n_samples) / sf

    # 出力配列
    result = np.full_like(data, np.nan, dtype=np.float64)

    for i in range(n_series):
        y = data[:, i]
        valid = ~np.isnan(y)
        if np.sum(valid) < degree + 1:
            continue  # 有効な点が少なすぎる場合はスキップ

        x_valid = t[valid]
        y_valid = y[valid]

        # 重み処理
        w_valid = np.full_like(y_valid, 1, dtype=np.float64)
        

        # スプラインフィッティング
        if np.isscalar(weights):
            spline = UnivariateSpline(x_valid, y_valid, w=w_valid, k=degree, s=weights)
        else:
            spline = UnivariateSpline(x_valid, y_valid, w=w_valid, k=degree, s=weights[i])
            
        result[:, i] = spline(t) if order == 0 else spline.derivative(order)(t)

    return result.squeeze()

# 運動学：位置から速度と加速度を計算
def kinematics(posi_vec, sf=sf, weights_a=weight_a, weights_v=weight_v):
    vel = smoothing_spline(posi_vec, weights = weights_v, sf = sf, order = 1)
    acc = smoothing_spline(posi_vec, weights = weights_a, sf = sf, order = 2)
    return vel, acc


# 曲率半径
def curvature_radius(vel, acc):
    return norm(vel)**3 / dot_product(acc, vel)

# 単位主法線ベクトル
def unit_principal_normal_vec(vel, acc):
    return cross_product(vel, cross_product(acc, vel)) / (norm(cross_product(acc, vel)) * norm(vel))[:,np.newaxis]

# 単位接線ベクトル
def unit_tangent_vec(vel):
    return vel / norm(vel)[:,np.newaxis]

# 曲率ベクトル
def curvature_vec(vel, acc):
    norm_part = norm(vel)**2 / norm(cross_product(acc, vel))**2
    return norm_part[:,np.newaxis] * cross_product(vel, cross_product(acc, vel))

################################
# Main
################################
data = data[1:]

release_frame = -10

vel, acc = kinematics(data, sf=sf, weights_a=weight_a, weights_v=weight_v)
vel_trim, acc_trim = vel[1:release_frame], acc[1:release_frame]
data_trim = data[1:release_frame]
curvature_radius1 = curvature_radius(vel_trim, acc_trim) # 曲率半径
unit_principal_normal_vec1 = unit_principal_normal_vec(vel_trim, acc_trim) # 単位主法線ベクトル
unit_tangent_vec1 = unit_tangent_vec(vel_trim) # 接線ベクトル
curvature_vec1 = data_trim + curvature_radius1[:,np.newaxis] * unit_principal_normal_vec1 # 曲率ベクトル

# 接線方向の加速度
acc_tangent = dot_product(acc_trim, unit_tangent_vec1)[:,np.newaxis] * unit_tangent_vec1

# 向心加速度
acc_centripetal = acc_trim - acc_tangent

# Create time array centered at release (t=0)
t = np.arange(len(vel_trim))/sf - len(vel_trim)/sf

# Create figure with two y-axes
fig, ax1 = plt.subplots()
ax2 = ax1.twinx()

# Plot velocity components on left axis (m/s)
ax1.plot(t, vel_trim, label=['x', 'y', 'z'])
ax1.plot(t, norm(vel_trim), 'k--', label='Norm speed')
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Velocity [m/s]')
ax1.set_title('Ball velocity')

# Plot velocity on right axis (km/h) 
ax2.plot(t, norm(vel_trim)*3.6, 'k--', alpha=0)  # Invisible plot to set scale
ax2.set_ylabel('Velocity [km/h]')
ax1.axvline(x=0, color='k', linestyle='--', alpha=0.5, label='Release')

# Add legend
ax1.legend()
plt.show()

################################
# 3D Plot
################################
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')
delete_frame = 3

# Plot data points (original trajectory)
ax.scatter(data_trim[:, 0], data_trim[:, 1], data_trim[:, 2], c='red', label='ball trajectory', s=2)

# Plot curvature vector points
ax.scatter(curvature_vec1[1:-delete_frame, 0], curvature_vec1[1:-delete_frame, 1], curvature_vec1[1:-delete_frame, 2], c='blue', label='center of curvature', s=5)

# Draw lines between corresponding points
for i in range(1, len(data_trim)-delete_frame):
    ax.plot([data_trim[i, 0], curvature_vec1[i, 0]], 
            [data_trim[i, 1], curvature_vec1[i, 1]], 
            [data_trim[i, 2], curvature_vec1[i, 2]], 
            'k-', linewidth=0.5, alpha=0.3)

# Plot acceleration vectors every 10 frames
for i in range(len(data_trim)-20, len(data_trim)-delete_frame, 2):
    # Scale factor for better visualization
    scale = 0.001
    
    # Plot tangential acceleration vector (red)
    ax.plot([data_trim[i, 0], data_trim[i, 0] + acc_tangent[i, 0]*scale],
            [data_trim[i, 1], data_trim[i, 1] + acc_tangent[i, 1]*scale],
            [data_trim[i, 2], data_trim[i, 2] + acc_tangent[i, 2]*scale],
            color='red', alpha=0.5, label='Tangential force' if i==len(data_trim)-20 else "")
              
    # Plot centripetal acceleration vector (blue) 
    ax.plot([data_trim[i, 0], data_trim[i, 0] + acc_centripetal[i, 0]*scale],
            [data_trim[i, 1], data_trim[i, 1] + acc_centripetal[i, 1]*scale],
            [data_trim[i, 2], data_trim[i, 2] + acc_centripetal[i, 2]*scale],
            color='blue', alpha=0.5, label='Centripetal force' if i==len(data_trim)-20 else "")

    # Plot total acceleration vector (orange)
    ax.plot([data_trim[i, 0], data_trim[i, 0] + acc_trim[i, 0]*scale],
            [data_trim[i, 1], data_trim[i, 1] + acc_trim[i, 1]*scale],
            [data_trim[i, 2], data_trim[i, 2] + acc_trim[i, 2]*scale],
            color='orange', alpha=0.5, label='Resultant force' if i==len(data_trim)-20 else "")


# Add 'Release' text annotation near the last point of data_trim
last_point = data_trim[-1]
# Add 'Release' text at the last point
ax.text(last_point[0], last_point[1], last_point[2], 'Release', fontsize=10)
# Add 'MER' text at the first point
first_point = data_trim[0]
ax.text(first_point[0], first_point[1], first_point[2], 'MER', fontsize=10)


ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
# Set the viewing angle
ax.view_init(elev=30, azim=170)  # elev: elevation angle, azim: azimuth angle

# Set z-axis minimum to 0
ax.set_zlim(bottom=0)

ax.set_aspect('equal')
ax.legend()
plt.show()

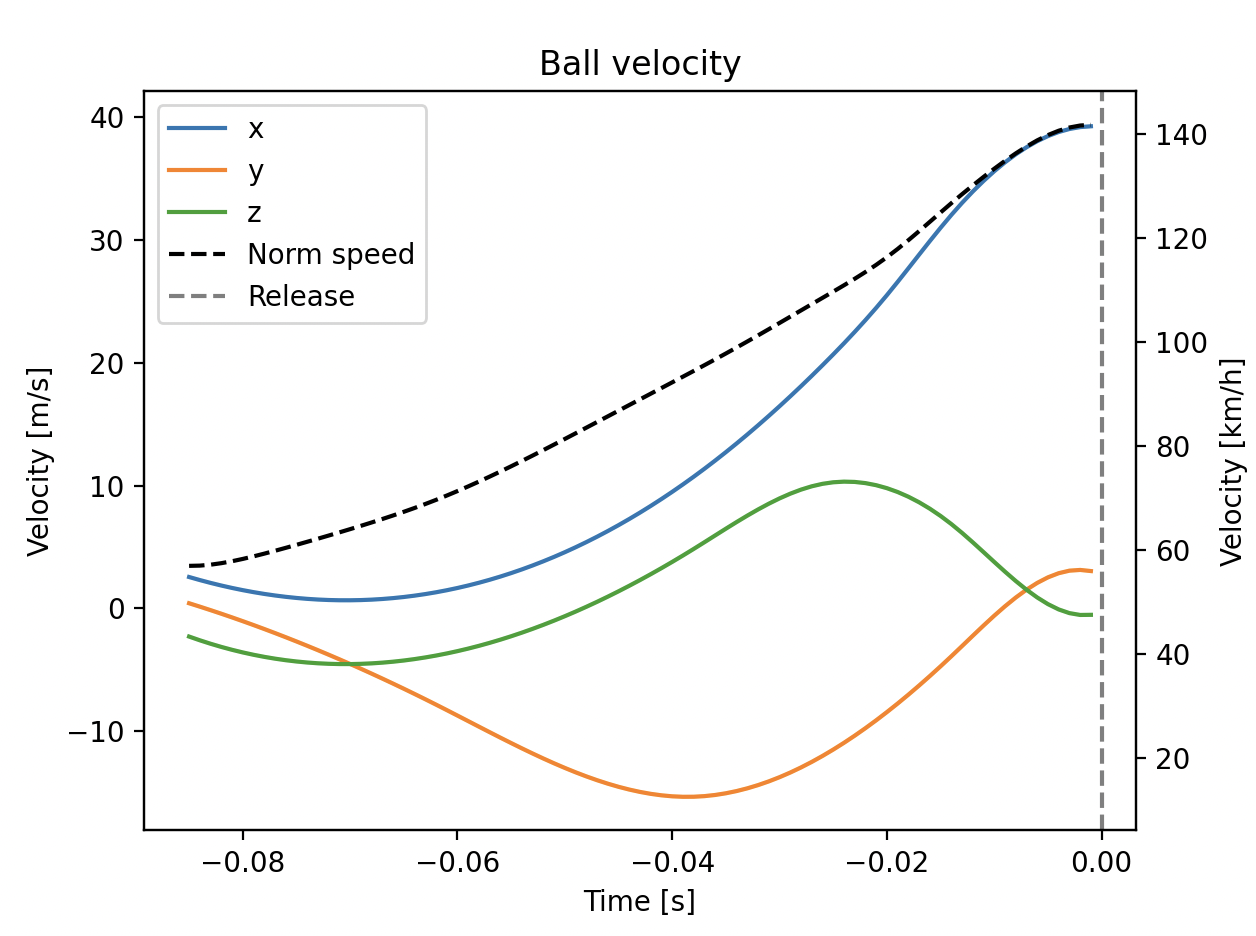
図７：ボールの速度

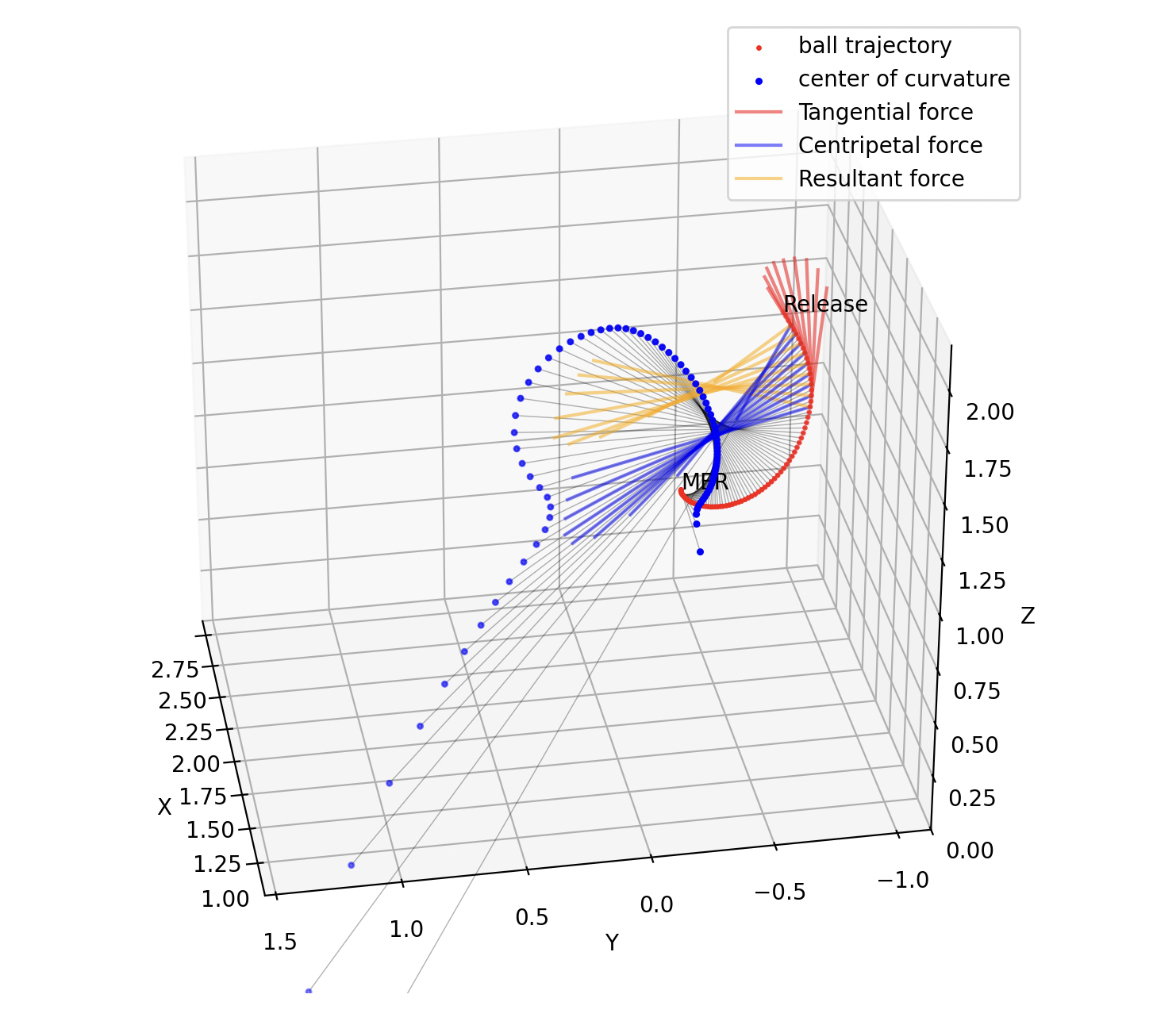
図８：ボールの軌道（赤），曲率中心（青），ボールに作用する接線方向の加速度（赤），
    　向心力加速度（青），総和の加速度（オレンジ）．加速度は2ms毎に描画．

これは斜め左後方から見た図である．Pythonコードで描けば自由に視点を変えられる（Jupyterでは不可）．

重力加速度は無視できるほど小さいので，オレンジ色の加速度は，ボールに作用する総和の力に相当すると考えてよい．また，この３つの加速度は，リリースの20ms前から2ms毎に描いているが，途中で向きが大きく変わっていることがわかる．ボールに作用する力のこの向きの変化は，バックスピンのトルクが作用し始めている（Qiita記事の動力学的回転開始を参照）ことを示している．

PyQtGraphでアニメーションを動かす（追記）

前のCodeで示していないが，アニメーションをPythonのJupyter・matplotlibベースで実現すると動作が重たい．これをPyQtGraphで実現するとOpenGLベースで動作が機敏⁹．コードは上記GitHubのリンクから．

まとめ

これまでバイオメカニクスや身体運動研究で，近似なしに厳密に，空間における曲率を計算している研究を見かけることはあまりないだろう．それは，身体運動における曲率中心の物理的な意味が十分に伝わっていない理由もあるだろうし，そもそもどのように計算を行えばよいか，教科書などの資料が乏しいことも理由として考えられる．

また，スカラの曲率やその逆数の曲率半径も重要だが，さらに空間における曲率中心の位置ベクトルが力学で重要な意味を持つことに気がついていないこともあるだろう．

ここでは，数理的な説明が中心であったが，またどこかで，身体運動における曲率中心の意味を述べていきたい．なお，これまでのボールの回転軸や力発揮効率との関係は，記事

や

なども参照していただければと思う．

また，MC19研究会では，ボールの回転軸や，ホームプレート上の投球誤差（ばらつき）がアームアングル（肩とボールを結ぶ直線の地面となす角度）ではなく，曲率中心とボールを結ぶ直線のなす角度で定まることを示した[文献2]．もちろんアームアングルの影響はあるが，プロ野球選手ともなると，体幹や下肢の動力をボールに伝えられるので，アームアングルが斜めに傾いていても，さらに縦回転に近づけることは可能である．

アームアングルだけでは，回転軸や回転による移動量は定まらないことに注意をされたい．

これらの内容については，またどこまで述べることとする．

補足

補足１：球速（速度の大きさ）の力学

図A1：ボールの速度（左）と加速度（右）．球速|v|は，何を積分することで計算される？

力学法則から当たり前だが，ボールに力を与えることでボールの速度が変化する．力が速度変化の源である．また，加速度の積分（加速度の時系列波形の面積）によって速度を計算でき，加速度は力を質量で割ったものであるから，重力加速度を無視すれば，加速度が速度を変化させる源といいかえることができる．

加速度を積分すれば速度になることはわかる．そこで，あらためて考えたいことは，「球速は，具体的に一体何を積分することで計算されるのか？」ということである．球速はスカラ値であって，ベクトルではない．加速度のxyz成分をそれぞれ積分すれば，xyzの速度となるが，速度ベクトルの向きは時々刻々変化する．加速度の大きさを積分しても球速（速度の大きさ）にはならない．

また，投球のように高速に運動するボールの運動の軌道が曲がる回転運動では，図６に示したように接線方向の加速度$a_{\parallel}$以外に，大きな向心力$a_{\perp}$が作用するため，速度方向と加速度方向は大きく異なる．

簡単な話のようで，このことは力学の教科書にもあまり出てこないし，自明ではなく意外とあまりよく理解されていないことかもしれない．

球速の定義

図A2：ボールの速度と加速度ベクトル

まず，モーションキャプチャのデータがあるとき，そもそもいわゆる球速がどのように計算されるか考える．

ボールの速度ベクトルとノルム（大きさ）は
$$
\begin{aligned}
\boldsymbol{v}(t) &= \begin{bmatrix} v_x(t) \\ v_y(t) \\ v_z(t) \end{bmatrix}
\\
|\boldsymbol{v}(t)| &= \sqrt{v_x (t)^2 + v_y (t)^2 + v_z (t)^2}
\end{aligned}
$$
と書くことができる．球速は速度ベクトルの大きさ$|\boldsymbol{v}(t)|$に相当する．ベクトルは３次元座標で３成分を持つわけだが，球速$|\boldsymbol{v}|$とは速度ベクトルの矢印の大きさ（ノルム）を意味し，スカラ値である．

このように球速の計算自体は簡単だ．しかし，球速に変化を与える加速度（力）は，どのように計算されるのだろうか？

球速の変化の源は何？

速度ベクトルは加速度ベクトル$\boldsymbol{a}(t)$の積分

$$
\boldsymbol{v}(T) = \int_0^{T} \boldsymbol{a}(t) dt + \boldsymbol{v}(0)
$$
で計算できる．球速$|\boldsymbol{v}|$はスカラ値である．繰り返し述べるが，何を積分すると，$|\boldsymbol{v}|$となるのだろうか？

$$
v=|\boldsymbol{v}| = \int ? ~dt + v(0)
$$

加速度$\boldsymbol{a}(t)$はベクトルだから，つまり，加速度ベクトルとそのノルムを

$$
\begin{aligned}
\boldsymbol{a}(t) &= \begin{bmatrix} a_x(t) \\ a_y(t) \\ a_z(t) \end{bmatrix}
\\
|\boldsymbol{a}(t)| &= \sqrt{a_x (t)^2 + a_y (t)^2 + a_z (t)^2}
\end{aligned}
$$
とすると，加速度ベクトル$\boldsymbol{a}(t)$を積分しても，ベクトルの３成分が計算されるだけだし，$|\boldsymbol{a}(t)|$を積分しても，球速$|\boldsymbol{v}(t)|$になるわけでもない．

球速というスカラの値は「何を積分すれば計算できる？」．この問いは，次のように言い換えることができる．つまり「球速を変化させる源の加速度とはどのようなスカラ値の加速度？」

図A3：球速＝接線方向の加速度の大きさの積分．

この答えは空間における曲率の力学に記述した，接線方向の加速度

$$
\begin{aligned}
\boldsymbol{a}_{\parallel} &= (\boldsymbol{a}^T \boldsymbol{T})\boldsymbol{T} = \left( \boldsymbol{a}^T \frac{\boldsymbol{v}}{|\boldsymbol{v}|} \right) \frac{\boldsymbol{v}}{|\boldsymbol{v}|}
\\
&= \frac{d}{dt}|\boldsymbol{v}| \boldsymbol{T}
\end{aligned}
$$
の式に記述している．このことを少し詳しく説明しよう，ここで，$\boldsymbol{T}=\frac{\boldsymbol{v}}{|\boldsymbol{v}|}$は，速度ベクトル方向の単位ベクトルである．

接線方向の加速度ベクトル$\boldsymbol{a}_{\parallel}$の大きさは，

加速度ベクトルの速度ベクトル方向の成分であるので，加速度$\boldsymbol{a}$と速度方向の単位ベクトル$\boldsymbol{T}$の内積$\boldsymbol{a}^T \boldsymbol{T}$によって計算される．これはスカラ値なので，これに速度方向の単位ベクトルをかけることで，接線方向の加速度ベクト$\boldsymbol{a}_{\parallel}$が計算される．

一方，２行目に書いているように，それは速度ベクトルの大きさの微分値に等しいことを意味する．速度ベクトルの大きさ$|\boldsymbol{v}|$とは球速を意味する．

接線方向の加速度の大きさ = スカラである球速の微分値

$$
|\boldsymbol{a}_{\parallel}| = \boldsymbol{a}^T \boldsymbol{T} = \boldsymbol{a}^T \left(\frac{\boldsymbol{v}}{|\boldsymbol{v}|} \right)= \frac{d}{dt}|\boldsymbol{v}|
$$

を意味する．これより，球速を変化させる源は，接線方向の加速度$\boldsymbol{a}^T \boldsymbol{T}$であり，$\boldsymbol{a}^T \boldsymbol{T}$を積分することで球速を計算できる．つまり，ボールの加速度$\boldsymbol{a}$（図A2の黄色）は速度方向$\boldsymbol{T}$とは全く異なる方向を向いているが，その加速度$\boldsymbol{a}$の，接線（速度）方向に沿った加速度成分（赤色）の大きさ$|\boldsymbol{a}_{\parallel}|=\boldsymbol{a}^T \boldsymbol{T}$が球速の変化に寄与する．つまり，

$$
v=|\boldsymbol{v}| = \int_0 |\boldsymbol{a}_{\parallel}|~dt + v(0)= \int_0 (\boldsymbol{a}^T \boldsymbol{T})~dt + v(0)
$$

と書ける．図A2のピンク色の面積（積分）が球速に相当する．

なお，これだけの議論から考えると，向心加速度$\boldsymbol{a}_{\perp}$は，直接的には球速と独立して定まるように見える．しかし，実際には向心加速度や向心力の大きさは，接線方向の加速度と無関係ではなく，両方とも角速度$\boldsymbol{\Omega}$で記述されることは，すでに示した．

向心力加速度$a_{\perp}$は回転を維持し，接線方向の加速度$a_{\parallel}$は純粋にボールを加速するために寄与する．また，角速度$\boldsymbol{\Omega}$やその変化は，接線方向の加速度と向心加速度の変化に寄与する．この数理を理解してしまえば，この結果は直感とも合うだろう．

参考文献

中内伸光，じっくりと学ぶ曲線と曲面−微分幾何学初歩−，共立出版
中内伸光，新装版　幾何学は微分しないと　〜微分幾何学入門〜，現代数学社
太田他，全身の力学によって拘束される投球のリリースタイミングと投球分布，MC19研究会，2025

３次元で関節に作用するトルクの計算では，二階微分の計算が伴う．このため，そもそもモーションキャプチャのデータなどが２点間距離の誤差で1mm以下など正確に計測が行われ，かつ平滑化スプラインのような正確で安定した微分を用いないと計算ができない．それと同様に，曲率中心もモーキャップなどで正確に速度と加速度が必要である． ↩
フレネ・セレの公式はネットでもヒットするが，大半が弧長パラメータ$s$による記述で，下記のWikiのように，時間のように一般パラメータ$t$で記述した式でないと，モーキャップデータから計算することはできない．曲率やフレネ・セレの公式については，WikiのOther expressions of the frameや，一橋大学の講義資料（幾何学I/II）を参照するとよいだろう．書籍としては，丁寧に解説された（ダジャレ付き），文献１，２を参照すると良い．note記事にも記述した． ↩
投球の場合，リリース直前を除けば重力はボールに作用する力に対して無視できるほど小さい． ↩
後半では，接線方向の力はさらに，オイラー力とコリオリ力に分解できることを示す． ↩
この記事では，時々ベクトルをイタリックの太字$\boldsymbol{a}_{\perp}$と表記すべきところを，Qiitaの不具合で，イタリックで表記することがあるので注意されたい． ↩
この名称はあまり普及した名称ではなく，一部のロボティクスや機械工学の研究者が使用する名称である． ↩
２つのベクトル$\pmb{a}, \pmb{b}$から構成されるベクトル三重積の大きさ$|\boldsymbol{b}\times (\boldsymbol{a} \times \boldsymbol{b})|$は$|\boldsymbol{b}| ~|\boldsymbol{a} \times \boldsymbol{b}|$と等しいことを利用した． ↩
曲線の曲がり具合だが，これを示すために弧長パラメータ$\pmb{s}$の導入が必要で，証明が長くなるので
こでは割愛したが，一橋大学講義資料「幾何学I/II」などを参照するとよいだろう． ↩
Cursor（Aiエディタ）の能力の凄さに驚く．ほぼLLMによる対話だけで，もとのPythonコードを変換してくれた．多くの修正は必要だが，コードを直接操作することはほとんどなかった．エンジニアからすると時代遅れのコメントだが，必要な機能を（悪く言えば勝手に）盛りこんだり，提案をしてくれ，変更の概要をまとめReadMeも書いてくれる．ただただ驚くだけである． ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up