Funnelアルゴリズムとは
Funnel(ファンネル)アルゴリズムとは___1辺を共有する三角形リストの始点から終点までの最短経路を求めるアルゴリズム___です。
ダイクストラ法やA*から得られた経路を平滑化する方法として使用されています。
Funnelは日本語で___漏斗___の意味です。
言葉通り漏斗をイメージしながら解いていくアルゴリズムです。
実装、記事にした理由
- ここ を参考にして実装したが動作しないパターンがあった
- Unityで使いたい
- 3次元に適用したい
- 日本語で詳説しているサイトが見つからなかった
大まかな流れ
- 与えられた三角形リストから3次元における左右の頂点配列を作成する
- 1で作成した配列をコピーしたものをXY平面の2次元に変換する
- 先端、左側の頂点リスト、右側の頂点リスト から形成されるFunnelを更新しながら経路を求める
- 求めた経路と三角形リストの連結部分(共有辺)の交点を挿入する
- 経路上の全ての点の法線を求める
- 3次元に復元する
- パスを生成する
解説
※この記事ではソースコード上でArray型となっているものを~配列、それ以外のコレクションを~リストと表記しています。
また、ベクトルやクオータニオンの演算に対してある程度知識があることを前提としています。
与えられた三角形リストから3次元における左右の頂点配列を作成する (CreateVertices3Dメソッド)
三角形リストから共有辺のリストを作成する
前後の三角形から共有辺を探してリストにします。共有辺が見つからない場合は連結してないので失敗とします。
始点を求めて、左右の3次元頂点配列に追加する
最初の三角形の頂点のうち、共有辺と向かい合う(共有辺に含まれない)頂点が始点となる
[赤]を左側の頂点、[青]を右側の頂点 とします。
共有辺の頂点が左右どちらの3次元配列の末尾と一致するかで左右に振り分けていく
この場合、現在の共有辺の下側の頂点が右側の頂点配列の末尾と一致するので、右側の頂点配列に追加します。
反対側の頂点は左側の頂点配列に追加します。
終点を求めて、左右の3次元頂点配列に追加する
始点同様、終点は最後の三角形の頂点のうち、直前の共有辺に向かい合う頂点を採用します。
最終的には以下のようになります。
※ここで重複する点を削除しないことが重要になります。
3次元配列を2次元配列にコピーする
先ほど作成した3次元配列のコピーを作成します。
コピーするだけなので2次元配列といってもこの段階では3次元座標が入っています。
3次元配列は2次元から3次元に復元する際に必要なので、そのまま保持します。
XY平面の2次元に変換する
先ほどコピーしたものを2次元に変換していきます。
最初の三角形の平面上に展開する (ConvertTo2Dメソッド)
イメージとしては三角形リストの連結部分(折れている箇所)を順番に伸ばして平行にしていく感じです。
起点となる点に対し、共有辺を軸として対象の点を回転させます。
対象の点を回転した後は、現在の共有辺以降の全ての頂点に同じ回転を適用させます。
これを始点まで繰り返すことで全ての頂点が同一平面上に展開されます。
※通常の展開図作成アルゴリズムでは重なりを考慮する必要がありますが、ここでは気にしなくて良い問題です。
XY平面に展開する (ConvertToXYPlane メソッド)
同一平面上に展開できたので、今度はXY平面上に変換します。
まずは始点を原点に移動する平行移動量と、現在の面をXY平面に重なるように回転する回転を求めます。
全ての頂点に対して求めた平行移動と回転を適用します。
Funnelを更新しながら2次元での経路を求める (UpdateFunnelメソッド)
これでFunnelアルゴリズムを適用する準備が整いました。
Funnelの先端、左側の頂点リスト、右側の頂点リストを初期化する
Funnelの先端(以下Apex)は次の情報を保持します
・2次元頂点配列のインデックス
・座標 (インデックスから所得できるが説明のしやすさのため)
・左か右かのフラグ
左右の頂点リストはそれぞれ対応するサイドの2次元頂点配列のインデックスをリストとして保持します。
最初のFunnelは次のようになります。
Apex → 始点
左側の頂点リスト → [1]
右側の頂点リスト → [1]
左右の頂点リストはそれぞれ対応するサイドの2次元頂点配列のインデックスをリストとして保持します。
最初のFunnelは次のようになります。
Apex → 始点
左側の頂点リスト → [1]
右側の頂点リスト → [1]
Funnelの左右交互に頂点を追加していく (Pushメソッド)
Funnelの左右どちらかの頂点リストを1つ進めます。
このとき2つのことをチェックします。1. Funnelが絞られないか (IsTightenedメソッド)
Funnelが絞られる場合は頂点リストを一度クリアしたあとに追加します。
なぜかというと、Apexから追加する頂点まで直進する場合に、現在のFunnelの壁と衝突することがないからです。Funnelが絞られるかの判定は
[1]のベクトルと [1]のベクトルの内積と
[2]のベクトルと [1]のベクトルの内積を比較します。
2. 反対の頂点リストを追い越さないか(IsCrossedOppositeVerticesメソッド)
反対側の頂点リストを追い越す場合は、追い越された頂点をApexに設定して、左右の頂点リストを初期化します
このとき以前のApexをリストに追加します
追い越しの判定は
Apexから反対側の頂点への[ベクトル]に対する 先端から対象の頂点への[ベクトル]の外積を比べることで判定します。
これを終点まで繰り返し、Apexの座標を結べば2次元での最短経路が求まります。
パスを生成する (MakePathメソッド)
処理の都合上、大まかな流れでの以下の工程をまとめて、パスを生成する工程とします。
- 求めた経路と三角形リストの連結部分(共有辺)の交点を挿入する
- 経路上の全ての点の法線を求める
- 3次元に復元する
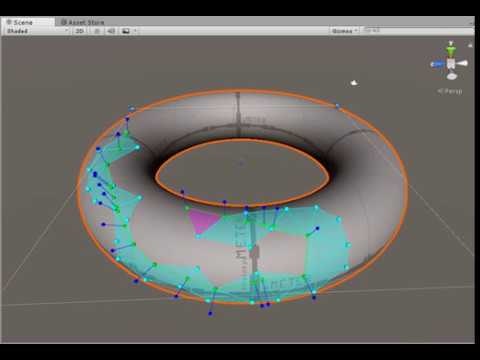
2次元の場合は必要ないですが、3次元の場合は求めた経路と共有辺の交点が必要になります。(理由はデモ動画をご覧いただければわかるかと思います)
交点の計算は単純に2直線の交点を求めるだけでよいのですが、3次元に復元するときにもとの座標を保持していないため工夫が必要です。
いろいろ方法はあると思うのですが、筆者がとった方法は、2次元上で片方の頂点からの距離の割合を保持しておき、3次元に復元した後に適用して交点を求める
方法を採用しました。
また、求めた経路上の法線も求めておくと何かと使えそうなので、一緒に法線も計算しています。
※法線の計算は言葉で説明するのが難しいのでコードを読んで頂いたほうが分かりやすいかと思います。
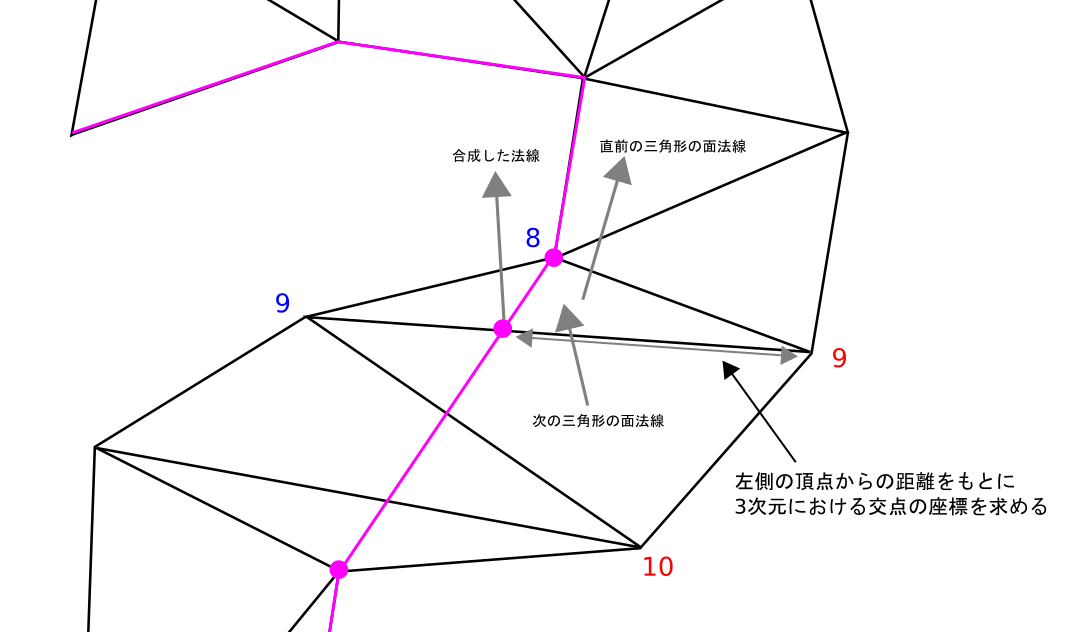
あとは、保持していた3次元頂点配列から対応する座標に変換して3次元に復元して完了です。
デモ
青色のラインは法線です。
プロジェクト
今回作成したプロジェクトをGitHubで公開しています。
※メインロジックはある程度テストして本記事に合わせてコメントを書いていますが、Editor拡張などの箇所は適当にサクッと実装したので挙動が不自然な箇所があります。
デモのモデルはProBuilderを使用しています。
ソースコード
一応メインのソースコードも載せておきます。
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
namespace FunnelAlgorithm
{
struct Apex
{
// 左側もしくは右側の頂点配列のインデックス
public int Index { get; private set; }
// 位置
public Vector3 Position { get; private set; }
// 左側か右側のフラグ
public bool IsLeft { get; private set; }
public Apex(int index, Vector3 position, bool isLeft)
{
Index = index;
Position = position;
IsLeft = isLeft;
}
}
public class Pathfinder
{
/// 3次元における左側の頂点配列
private Vector3[] leftVertices3d;
/// 3次元における右側の頂点配列
private Vector3[] rightVertices3d;
/// 2次元における左側の頂点配列
private Vector3[] leftVertices2d;
/// 2次元における右側の頂点配列
private Vector3[] rightVertices2d;
/// Funnelの先端
private Apex apex;
/// Funnelの右側の頂点リスト
private List<int> leftIndices = new List<int>();
/// Funnelの左側の頂点リスト
private List<int> rightIndices = new List<int>();
/// Funnelの先端リスト
private List<Apex> apexes = new List<Apex>();
public Path FindPath(IEnumerable<Triangle> triangles)
{
// 三角形の数が2つ未満の場合は計算できないので空のパスを返す
if (triangles.Count() < 2)
return null;
// 与えられた三角形リストから3次元における左右の頂点配列を作成する
if (!CreateVertices3D(triangles))
return null;
// 3次元における頂点配列を2次元における頂点配列にコピーする
CopyVertices3DToVertices2D();
// コピーした頂点配列を2次元に変換する
ConvertTo2D();
// XY平面上に変換する
ConvertToXYPlane();
// Funnelの先端を始点にセットする (右側も左側も同じなのでどっちを採用してももいい。ここでは左側を採用)
apex = new Apex(0, leftVertices2d[0], true);
// Funnelの左側の頂点リストに最初の頂点を追加する(先端から1つ進んだとこから開始する)
leftIndices.Add(1);
// Funnelの右側の頂点リストに最初の頂点を追加する(先端から1つ進んだとこから開始する)
rightIndices.Add(1);
// 終点にたどり着くまでFunnelに頂点を追加していく
while (UpdateFunnel()) { }
// 終点にたどり着いたら現在のFunnelの先端を追加する
apexes.Add(apex);
// 終点を追加する(ここも左、右側のどちらを採用してもOK)
apexes.Add(new Apex(leftVertices2d.Length - 1, leftVertices2d.Last(), true));
// 共有辺との交点()を求め、最終的なパスを計算する
var path = MakePath();
return path;
}
private bool CreateVertices3D(IEnumerable<Triangle> triangles)
{
// 三角形リストから共有辺のリストを作成する
var commonEdges = new List<Edge>();
foreach (var pair in triangles.MakePairs())
{
// 前後の三角形から共有辺を探す
var commonEdge = pair.Left.FindCommonEdge(pair.Right);
if (commonEdge == null)
{
// 共有辺が見つからない場合は連結してないので失敗
return false;
}
commonEdges.Add(commonEdge);
}
// 3次元における頂点配列を初期化する。 長さは 始点 + 終点 + 共有辺の数 になる
leftVertices3d = new Vector3[commonEdges.Count + 2];
rightVertices3d = new Vector3[commonEdges.Count + 2];
// 始点を求める。始点は最初の三角形の頂点の内、最初の共有辺に向かいあう頂点
var startPoint = triangles.First().FindOppositeVertex(commonEdges.First()).Value;
// 始点を両サイドの頂点配列に追加
leftVertices3d[0] = rightVertices3d[0] = startPoint;
// 共有辺の頂点を左、右に分けていく
var i = 1;
foreach (var commonEdge in commonEdges)
{
var nextOrigin = Vector3.zero;
if (i == 1)
{
leftVertices3d[i] = commonEdge.A;
rightVertices3d[i] = commonEdge.B;
nextOrigin = leftVertices3d[i];
}
else
{
// 頂点配列の最後と一致するかを調べて一致する場合はそのサイドに配列に追加する。一致しないほうは逆サイドに追加する。 必ずどちらかに一致する
if (commonEdge.A.Equals(leftVertices3d[i - 1]) || commonEdge.B.Equals(rightVertices3d[i - 1]))
{
leftVertices3d[i] = commonEdge.A;
rightVertices3d[i] = commonEdge.B;
nextOrigin = rightVertices3d[i];
}
else
{
leftVertices3d[i] = commonEdge.B;
rightVertices3d[i] = commonEdge.A;
nextOrigin = leftVertices3d[i];
}
}
i++;
}
// 終点を求める。終点は最後の三角形の頂点の内、最後の共有辺に向かいある頂点
var endPoint = triangles.Last().FindOppositeVertex(commonEdges.Last()).Value;
// 終点を両サイドの頂点配列に追加
leftVertices3d[leftVertices3d.Length - 1] = rightVertices3d[leftVertices3d.Length - 1] = endPoint;
return true;
}
private void CopyVertices3DToVertices2D()
{
// 3次元における頂点配列をそのままコピーする
// コピーしたものをあとで2次元に変換する
leftVertices2d = leftVertices3d.Select(v => new Vector3(v.x, v.y, v.z)).ToArray();
rightVertices2d = rightVertices3d.Select(v => new Vector3(v.x, v.y, v.z)).ToArray();
}
private void ConvertTo2D()
{
var origin = leftVertices2d[0];
for (int i = 2, count = leftVertices2d.Length; i < count; i++)
{
// 回転対象の頂点をもとめる
var isLeftEqual = leftVertices2d[i].Equals(leftVertices2d[i - 1]);
var target = isLeftEqual ? rightVertices2d[i] : leftVertices2d[i];
// origin - edge 平面の法線
var originNormal = Vector3.Cross(leftVertices2d[i - 1] - rightVertices2d[i - 1], origin - leftVertices2d[i - 1]).normalized;
// target - edge 平面の法線
var targetNormal = Vector3.Cross(rightVertices2d[i - 1] - leftVertices2d[i - 1], target - rightVertices2d[i - 1]).normalized;
// 2つの法線間の角度を求める
var angle = MathUtility.SignedVectorAngle(originNormal, targetNormal, leftVertices2d[i - 1] - rightVertices2d[i - 1]);
// edge を軸としてangleだけ回転するQuaternionを求める
var rotation = Quaternion.AngleAxis(angle, rightVertices2d[i - 1] - leftVertices2d[i - 1]);
// 回転軸に回転を適用して平行移動量を求める
var translation = leftVertices2d[i - 1] - (rotation * leftVertices2d[i - 1]);
for (int j = i; j < leftVertices2d.Length; j++)
{
// 求めた変換パラメータを現在の頂点以降の頂点全てに適用する
// 適用する順番は回転->平行移動の順にすること
leftVertices2d[j] = rotation * leftVertices2d[j];
leftVertices2d[j] = leftVertices2d[j] + translation;
rightVertices2d[j] = rotation * rightVertices2d[j];
rightVertices2d[j] = rightVertices2d[j] + translation;
}
// 次の回転の起点を求める
var nextOrigin = isLeftEqual ? rightVertices2d[i - 1] : leftVertices2d[i - 1];
origin = nextOrigin;
}
}
private void ConvertToXYPlane()
{
// 始点を原点に移動するパラメータを求める
var origin = leftVertices2d[0];
var translation = Vector3.zero - origin;
var normal = Vector3.Cross(leftVertices2d[1] - origin, rightVertices2d[1] - origin).normalized;
var rotation = Quaternion.FromToRotation(normal, new Vector3(0, 0, 1));
// 全ての頂点に対してパラメータを適用する
for (int i = 0; i < leftVertices2d.Length; i++)
{
leftVertices2d[i] = rotation * leftVertices2d[i];
leftVertices2d[i] = leftVertices2d[i] + translation;
leftVertices2d[i] = new Vector3(leftVertices2d[i].x, leftVertices2d[i].y);
rightVertices2d[i] = rotation * rightVertices2d[i];
rightVertices2d[i] = rightVertices2d[i] + translation;
rightVertices2d[i] = new Vector3(rightVertices2d[i].x, rightVertices2d[i].y);
}
}
private Path MakePath()
{
var positions = new List<Vector3>();
var normals = new List<Vector3>();
// 先端リストの前後でペアを作成してループで回す
foreach (var pair in apexes.MakePairs())
{
// 現在の先端の頂点インデックスを開始インデックスとする
var startIndex = pair.Left.Index;
// 次の先端の頂点インデックスを終了インデックスとする
var endIndex = pair.Right.Index;
// 現在の先端のポジション(3次元)をパスに追加
var startPoint = (pair.Left.IsLeft ? leftVertices3d : rightVertices3d)[pair.Left.Index];
positions.Add(startPoint);
// 現在の先端の法線を求める
if (startIndex == 0)
{
// 始点の場合
normals.Add(Vector3.Cross(rightVertices3d[1] - leftVertices3d[1], rightVertices3d[1] - leftVertices3d[0]).normalized);
}
else
{
var opposite = rightVertices3d[startIndex].Equals(rightVertices3d[startIndex - 1]) ? leftVertices3d[startIndex - 1] : rightVertices3d[startIndex - 1];
normals.Add(Vector3.Cross(rightVertices3d[startIndex] - leftVertices3d[startIndex], rightVertices3d[startIndex] - opposite).normalized);
}
// 開始インデックスから終了インデックスまでの共有辺との交点を求める
foreach (var i in Enumerable.Range(startIndex + 1, endIndex - startIndex))
{
Vector3 intersection;
// 現在の先端 - 次の先端 の線分と 共有辺との交点を求める
if (MathUtility.SegmentSegmentIntersection(out intersection, pair.Left.Position, pair.Right.Position, leftVertices2d[i], rightVertices2d[i]))
{
// 後から3次元に変換できるように共有辺の左側の頂点から交点までの長さを割合として計算する
var lerp = Vector3.Distance(intersection, leftVertices2d[i]) / Vector3.Distance(rightVertices2d[i], leftVertices2d[i]);
// 各サイドの3次元における頂点を取得
var left3dpos = leftVertices3d[i];
var right3dpos = rightVertices3d[i];
// 先ほど求めた割合から3次元における交点を算出する
var position = Vector3.MoveTowards(left3dpos, right3dpos, Vector3.Distance(left3dpos, right3dpos) * lerp);
// 現在の面の法線を求める
var currentOpposite = rightVertices3d[i].Equals(rightVertices3d[i - 1]) ? leftVertices3d[i - 1] : rightVertices3d[i - 1];
var currentNormal = Vector3.Cross(rightVertices3d[i] - leftVertices3d[i], rightVertices3d[i] - currentOpposite);
// 次の面の法線を求める
var nextOpposite = rightVertices3d[i + 1].Equals(rightVertices3d[i]) ? leftVertices3d[i] : rightVertices3d[i];
var nextNormal = Vector3.Cross(rightVertices3d[i + 1] - leftVertices3d[i + 1], rightVertices3d[i + 1] - nextOpposite);
var normal = new Vector3((currentNormal.x + nextNormal.x) / 2.0f, (currentNormal.y + nextNormal.y) / 2.0f, (currentNormal.z + nextNormal.z) / 2.0f).normalized;
// パスに追加
positions.Add(position);
normals.Add(normal);
}
}
}
// 3次元における終点をパスに追加
var endPoint = leftVertices3d[leftVertices3d.Length - 1];
positions.Add(endPoint);
// 終点の法線を求める
var endNormal = Vector3.Cross(leftVertices3d[leftVertices3d.Length - 2] - rightVertices3d[rightVertices3d.Length - 2], leftVertices3d[leftVertices3d.Length - 2] - leftVertices3d.Last()).normalized;
normals.Add(endNormal);
return MakePath(positions, normals);
}
private Path MakePath(IEnumerable<Vector3> positions, IEnumerable<Vector3> normals)
{
// 同じポジションでグループ化する
var positionGroups = positions.SplitByEquality();
// 法線を合成する
var resultNormals = new List<Vector3>();
int skipCount = 0;
foreach (var g in positionGroups)
{
// ポジションリストに対応する法線リストを取得して合成する
var resultNormal = MathUtility.Synthesize(normals.Skip(skipCount).Take(g.Count()));
resultNormals.Add(resultNormal);
skipCount += g.Count();
}
var resultPositions = positionGroups.Select(g => g.First());
return new Path(resultPositions.Reverse<Vector3>(), resultNormals.Reverse<Vector3>());
}
private bool UpdateFunnel()
{
// Funnelの左側の頂点リストが終点にたどり着いたら終了 (右側も終点になるはずなので左側のチェックでよい)
if (leftVertices2d.Length - 1 <= leftIndices.Last())
return false;
// Funnelの左側に頂点を追加する
if (Push(leftVertices2d, rightVertices2d, ref leftIndices, ref rightIndices, true))
{
// 左側に追加できた場合は右側に追加する
Push(rightVertices2d, leftVertices2d, ref rightIndices, ref leftIndices, false);
}
return true;
}
private bool Push(Vector3[] targets, Vector3[] opposites, ref List<int> targetIndices, ref List<int> oppositeIndices, bool isLeft)
{
// 進めた際にFunnnelの反対側の頂点リストを追い越さないかを調べる
var crossedIndex = IsCrossedOppositeVertices(targets, opposites, targetIndices, oppositeIndices);
if (crossedIndex > 0 && crossedIndex < targets.Count() - 1)
{
// 追い越した場合は現在のFunnelの先端を記録する
apexes.Add(apex);
// Funnelの先端を追い越されたほうの頂点にセットする
apex = new Apex(crossedIndex, opposites[crossedIndex], !isLeft);
// Funnelの両サイドのインデックスをセットする
var nextIndex = apex.Index + 1;
while (opposites.Length > nextIndex)
{
// Funnelの先端と同じ座標にいる場合は座標が変わるまでインデックスを進める
if (!apex.Position.Equals(opposites[nextIndex]))
break;
nextIndex++;
}
targetIndices = new List<int>() { nextIndex };
oppositeIndices = new List<int> { nextIndex };
// 進めることができなかったのでFalseを返す
return false;
}
// 進めることができる
var next = targetIndices.Last() + 1;
// 進めた場合Funnelが絞られるかを調べる
if (IsTightened(targets, opposites, targetIndices, oppositeIndices))
{
// Funnelが絞られるので一度頂点リストをクリアする
targetIndices.Clear();
}
// 新しい頂点として追加
targetIndices.Add(next);
// 進めることができたのでTrueを返す
return true;
}
private bool IsTightened(Vector3[] targets, Vector3[] opposites, List<int> targetIndices, List<int> oppositeIndices)
{
// 先端から、進める側の最後の頂点に向かうベクトル
var lastVec = (targets[targetIndices.Last() + 1] - apex.Position).normalized;
// 先端から、進める側の最初の頂点に向かうベクトル
var firstVec = (targets[targetIndices.First()] - apex.Position).normalized;
// 先端から、反対側の最初の頂点に向かうベクトル
var oppositeVec = (opposites[oppositeIndices.First()] - apex.Position).normalized;
return Vector3.Dot(lastVec, oppositeVec) > Vector3.Dot(firstVec, oppositeVec);
}
private int IsCrossedOppositeVertices(Vector3[] targets, Vector3[] opposites, List<int> targetIndices, List<int> oppositeIndices)
{
// 先端から、進める側の最後の頂点に向かうベクトル
var lastVec = targets[targetIndices.Last()] - apex.Position;
// 先端から、進める側の追加する頂点に向かうベクトル
var nextVec = targets[targetIndices.Last() + 1] - apex.Position;
foreach (var i in oppositeIndices)
{
// 先端から、反対側のi番目の頂点に向かうベクトル
var oppositeVec = opposites[i] - apex.Position;
if (IsCrossed(oppositeVec, lastVec, nextVec))
return i;
}
return 0;
}
private bool IsCrossed(Vector3 target, Vector3 current, Vector3 next)
{
// 不正なベクトルの場合はダメ
if (target == Vector3.zero || current == Vector3.zero || next == Vector3.zero)
return false;
// 更新前のベクトルと基準となるベクトルの外積をとる
var currentCross = Vector3.Cross(target, current).normalized;
// 更新後のベクトルと基準となるベクトルの外積をとる
var nextCross = Vector3.Cross(target, next).normalized;
var dot = Vector3.Dot(currentCross, nextCross);
// 外積が反対方向なら追い越したことになる
return dot <= 0;
}
}
}
最後に
今回記事を書くにあたって、説明しやすいように処理を冗長に書いたり、変数を多くしたりしているので、最適化の余地がかなりあります。(左右の配列をまとめるなど)
また、Funnelアルゴリズムを3Dに適用するロジックは筆者が考えたものであり、他に最適なアルゴリズムが存在するかもしれません。
あくまで1つの方法として捉えて頂ければと思います。