1. 概要
1-1. 経緯
kaggleでテーブルデータを扱っていた。
モデルの精度向上のためにスコアの高い人のやり方をみたところ、説明変数の歪度(skewness)を操作している前処理を見つけた。
自分も歪度に対する前処理を使ってみようと思ったのだけど、一見して処理内容が理解できなかったので調査した。
1-2. 調べたこと
具体的には、以下の内容を調査した。
- kaggleで使用されていた、歪度(skewness)に対する前処理の内容
- 前処理で使用されている二つの関数の処理
- scipy.special.boxcox1p
- spicy.stats.boxcox_normmax
- XGBoostとLASSO回帰における、上記前処理の有効性
1-3. 結論
わかったこと
- 統計の領域には
Box-Cox変換と呼ばれるものがある -
Box-Cox変換は、(雑に言うと)歪んだ分布を正規分布の形に近づけるために用いられたりする - Box-Cox変換にはパラメータ:lambda($\lambda$)を指定する必要があるが、Pythonなら
spicy.stats.boxcox_normmaxを使ってlambda($\lambda$)を最適化できる - XGBoostモデルを使うときは、Box-Cox変換を適用しても効果がない
- LASSO回帰モデルを使うときは、Box-Cox変換すると、とても効果がある!!
2. お手本にしたやり方
ちなみに自分が見たのはこのお二方のやり方。
2-1. Nanashi さん
Full metal alchemist好きのようだ。ほっこり。
2-2. Nitesh Chaudhry さん
2-3. お二人が使っていた処理
from scipy.stats import skew, boxcox_normmax from scipy.special import boxcox1p numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64'] numerics2 = [] for i in features.columns: if features[i].dtype in numeric_dtypes: numerics2.append(i) skew_features = features[numerics2].apply(lambda x: skew(x)).sort_values(ascending=False) high_skew = skew_features[skew_features > 0.5] skew_index = high_skew.index for i in skew_index: features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))
skewnessに対する二人の前処理をよく見たら、全く同じだった。
kaggleではよく利用される処理なのかな。。。
kaggleでいいスコアを出したければ、skewnessと向き合ってみてもいいのかもしれない。
というわけで、skewnessそのものについても調べてみようっと。
3. 歪度(skewness)
この歪度、統計検定の勉強するときにサラっと見たんですけどね。
全く理解してませんでしたよっと。(2級では出てこないからか?)
そんな方用の復習です。
理解している方は飛ばしてください。
3-1. 歪度のイメージを掴む
百聞は一見に...
ということで、様々な歪度のデータを視覚化してみました。
| 歪度 (skewness) |
分布のヒストグラム | 備考 |
|---|---|---|
| 2.36 |  |
kaggke House Priceの OpenPorchSF 列 |
| 0.92 |  |
〃の BsmtUnfSF 列 |
| 0.68 |  |
〃の TotRmsAbvGrd 列 |
| 0.04 |  |
〃の FullBath 列 |
| -0.50 |  |
〃の YearRemodAdd 列 |
| -1.81 | 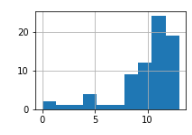 |
自作データ |
値が0以上なら分布が左寄りに、0以下なら分布が右寄りになると言われているのですが、正にその通りになってました。
歪度0.04のチャートはスカスカすぎて、ちょっとイメージを掴むのに適さないかもですが、現実のデータはこういうのもあるということで(^ワ^*)
3-2. 歪度 > 0.5とは
「2-3. お二人が使っていた処理」のところに、
high_skew = skew_features[skew_features > 0.5]
という処理があり、ここでは歪度0.5超の列のみが絞り込まれています。
この「歪度0.5超」ということの意味があまり沸いてなかったのですが、「3-1.」の調査によっておぼろげにイメージできました。
House Priceの説明変数の分布が左に偏りがちなので、左に偏っている列だけを今回の前処理の対象として絞り込んでいたようですね。
4. 処理をよく見てみる
4-1. お手本の処理
お二人が使っていた処理を一つ一つ解読すると、こんな感じになる。
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numerics2 = []
# NOTE: 数値型の列名をだけを`numerics2`という配列変数に代入
for i in features.columns:
if features[i].dtype in numeric_dtypes:
numerics2.append(i)
# NOTE: 各列のskewnessを計算して配列にした後、skewnessの大きい順にソートする
skew_features = features[numerics2].apply(lambda x: skew(x)).sort_values(ascending=False)
# NOTE: `skewness`が`0.5`を超える列だけに絞り込む
high_skew = skew_features[skew_features > 0.5]
# NOTE: `skewness`が`0.5`を超える列の列名を取得
skew_index = high_skew.index
# NOTE: `skewness`が`0.5`を超える各列に対して以下の前処理
# boxcox_normmax:
# 正規分布になるべく近づけるような `lambda` を計算
# boxcox1p:
# `lambda` をパラメータとして利用して、各列の分布が正規分布に近づくように変換をかける
for i in skew_index:
features[i] = boxcox1p(features[i], boxcox_normmax(features[i] + 1))
後半で、BoxCox変換処理というものが出てくる。
BoxCox変換というものが一体何なのかについては、以下のような記事を見てもらえたらと思うのですが、
ざっくり言うと、BoxCox変換を使うと正規分布に従わないデータの分布を正規分布に近づける効果があるようです。
4-2. 比較対象
この辺の記事を見ると、BoxCox変換ではなくて、np.log1pが使われています。
もしかしたらBoxCox変換じゃなくてnp.log1pでもいいのかも?
ということで、両方の変換処理の結果を比較してみました。
ソースコードが気になる方は以下を展開してくださいな。
ソースコード
from typing import Any, Callable, Dict, List, Tuple
import numpy as np
import pandas as pd
from scipy.stats import skew, boxcox_normmax
from scipy.special import boxcox1p
def load_data() -> Tuple[pd.DataFrame, pd.DataFrame]:
"""
house priceのデータを読み込み
"""
train = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/train.csv')
test = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/test.csv')
return train, test
def transform_with_boxcox(df: pd.DataFrame):
"""
データにboxcox変換をかける
"""
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric_cols = [
col for col in df.columns
if df[col].dtype in numeric_dtypes
]
print(len(numeric_cols), numeric_cols)
skew_features = df[numeric_cols].apply(lambda x: skew(x)).sort_values(ascending=False)
high_skew = skew_features[skew_features > 0.5]
skew_index = high_skew.index
print(len(skew_index), skew_index)
for i in skew_index:
df[i] = boxcox1p(df[i], boxcox_normmax(df[i] + 1))
return df
def transform_with_log1p(df: pd.DataFrame):
"""
データにnp.log1pで変換をかける
"""
numeric_dtypes = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
numeric_cols = [
col for col in df.columns
if df[col].dtype in numeric_dtypes
]
print(len(numeric_cols), numeric_cols)
skew_features = df[numeric_cols].apply(lambda x: skew(x)).sort_values(ascending=False)
high_skew = skew_features[skew_features > 0.5]
skew_index = high_skew.index
print(len(skew_index), skew_index)
for i in skew_index:
df[i] = np.log1p(df[i])
return df
# 実験開始
train, test = load_data()
df_boxcox: pd.DataFrame = transform_with_boxcox(train.copy())
df_log: pd.DataFrame = transform_with_log1p(train.copy())
numeric_dtypes: List[str] = ['int16', 'int32', 'int64', 'float16', 'float32', 'float64']
num_cols: List[str] = [
col for col in train.columns
if train[col].dtype in numeric_dtypes
]
# 結果表示用のDataFrame作成
df_skew_investigation = pd.DataFrame({
'name': num_cols,
'original_skew': skew(train[num_cols]),
'skew_after_boxcox': skew(df_boxcox[num_cols]),
'skew_after_log1p': skew(df_log[num_cols]),
})
print(df_skew_investigation[df_skew_investigation['original_skew'] > 0.5])
結果は以下の通り。
| 列名 | 内容 |
|---|---|
| original_skew | 元データのskewness |
| skew_after_boxcox | boxcox変換後のskewness |
| skew_after_log1p | np.log1pで変換した場合のskewness |
name original_skew skew_after_boxcox skew_after_log1p
0 MSSubClass 1.406210 0.431145 0.248741
2 LotArea 12.195142 -0.185294 -0.137263
4 OverallCond 0.692355 0.335371 -0.253754
8 BsmtFinSF1 1.683771 0.381851 -0.617774
9 BsmtFinSF2 4.250888 2.645006 2.521100
10 BsmtUnfSF 0.919323 0.053031 -2.184257
11 TotalBsmtSF 1.522688 0.452285 -5.149373
12 1stFlrSF 1.375342 -0.006599 0.080032
13 2ndFlrSF 0.812194 0.883107 0.289346
14 LowQualFinSF 9.002080 7.392523 7.452650
15 GrLivArea 1.365156 0.005867 -0.006134
16 BsmtFullBath 0.595454 0.590504 0.418782
17 BsmtHalfBath 4.099186 3.925130 3.929022
19 HalfBath 0.675203 0.711553 0.565586
21 KitchenAbvGr 4.483784 3.953381 3.865437
22 TotRmsAbvGrd 0.675646 0.040872 -0.058198
23 Fireplaces 0.648898 0.514500 0.181896
27 WoodDeckSF 1.539792 0.776782 0.153379
28 OpenPorchSF 2.361912 0.624656 -0.023373
29 EnclosedPorch 3.086696 2.285796 2.110104
30 3SsnPorch 10.293752 7.744137 7.727026
31 ScreenPorch 4.117977 3.328194 3.147171
32 PoolArea 14.813135 14.476284 14.348342
33 MiscVal 24.451640 5.199813 5.165390
36 SalePrice 1.880941 0.029469 0.121222
こうしてみてみると、np.log1pで変換した場合、変換が効き過ぎて右に偏ったりしてることがある。
BsmtUnfSFとかTotalBsmtSFとか。
元々skewnessプラスだったのがマイナスに振り切れちゃってますね。
逆に、boxcoxだとあんまり偏りが緩和されてなくて、左に偏ったままだったりすることもあるみたい。
2ndFlrSFとかがそう。
それぞれ一長一短ある模様。
5. 精度への影響を確認
5-1. XGBoost
XGBoostでHouse Priceのデータを学習させるときに、上記「4.」で確認した
- BoxCox変換
- np.log1pによる変換
どちらが良い結果になるのか確認した。
結果はなんと...
どちらを使っても(どちらも使わなくても)スコアは1ミリも変わらず!(´^ω^`)ブフォwww
がっかり!!!!!!
どうやら、XGBoostにとっては説明変数のデータの分布がいくら歪んでようが関係ないみたいです。
補足
ちなみに、目的変数に対する対数変換は、XGBoostを使う場合にも効果があります。
SalePrice列に対してnp.logをかけた上で学習 / 推論し、提出前データにnp.expをかけてあげるとスコアが結構改善します。
今回わかったのは、説明変数を正規分布に近づけても、XGBoostにとっては効果がない、ということでした。
5-2. LASSO回帰
う~ん。。。これだけだと記事にする価値がないw(´;ω;`)ブワッ
と思ったので、今回の変換処理の有無がどう影響するか、LASSO回帰で改めて試してみます。
最初はLASSO回帰試すつもりなかったんですが。
勉強になるからまあいいか!!(^ワ^*)
というわけで、ある程度前処理しておいたデータに対してそれぞれの変換処理を試してみると、以下の結果に。
| モデル | 説明変数に対する変換処理 | RSME |
|---|---|---|
| sklearn.linear_model.LassoCV | なし | 0.133 |
| 〃 | BoxCox変換 | 0.119 |
| 〃 | log1pによる変換 | 0.124 |
なんか、超改善しました。
XGBoostより圧倒的に成績がよくなりました。
(これまでの私の、XGBoostをcross_validationにかけた結果のRSMEのベストは0.135でした。あっさり負けた。)
6. 感想
6-1. skewnessについて
統計学に出てくる歪度(skewness)って「いつ使うんだろう?」「勉強しても使わなくない?」と思ってたけど、初めて実務に活かせる気がしてきた。
そのうち、尖度(kurtosis)を分析に活用する日も来るかな?
大学とか大学院で統計を専攻してる人は、歪度とか尖度使って分析してたりするんだろうか?
6-2. LASSO回帰について
この記事の主題ではないんですが。。。
LASSO回帰とBoxCox変換は非常に相性が良さそうです!!!
単に、House Priceタスクのデータとの兼ね合いの方が影響が大きい可能性もありますが、だとしても結構な改善幅だと思います。
テーブルデータに対してはまずLightGBM、XGBoost を使おうとよく言われますが、LASSO回帰andBoxCox変換も是非試したいですね。
色々なモデルを試してみることの重要性を知りました。
7. 参考にした記事
関数の公式リファレンス
その他関連記事
kaggle優秀者の公開notebook
BoxCox変換
LASSO回帰