scikit-learnなどを使うとさくっと利用できてしまうk平均法を、アルゴリズム理解と勉強のため、自分でPythonを使って書いていってみます。
k平均法とは
k平均法(英語ではk-means clustering)とは、クラスタリング(データの特徴に応じたグループ分け)のアルゴリズムの一つです。
参考 : k平均法 - Wikipedia
クラスタリングのグループの1つ1つをクラスター(cluster)と呼びます。
k平均法では各クラスターの平均を用いた計算を行い、k個のクラスターにデータを分類行うためk-means clusteringという名前になっています。
k平均法の特徴と活用の一例
k平均法のクラスタリングはデータさえあれば実行することができます。
いわゆる教師無し学習といった挙動をするので、正解ラベルなどを用意する必要がありません。
そのためデータだけある状態で、データの傾向の把握などに利用することができます。
たとえば、どんな傾向のユーザーグループが存在するのかを把握し、施策をそれぞれに向けて分けるといったケースに使うことができます。
一方で計算内容の都合で、通常のk平均法ではクラスター数を事前に自分で決める必要があります。そのため「実はクラスター数が7個が最適だったのにクラスター数を5個に設定していた」といったケースが発生しうるアルゴリズムになります。
また、各値の平均やクラスターとの距離などを利用する計算なので、値の中に異常値が含まれていて且つクラスターの初期位置が異常値の近くになってしまうと、そこでクラスターが固定されてしまうケースがある(異常値に弱い)といった特徴も持ちます。
それらを解決するためのk-means++やx-meansといったアルゴリズムも存在しますが、本記事ではそこまでは触れません。
k平均法の計算方法
k平均法は以下のような流れの計算を行います。
- [1]. クラスタリングを反映したいデータを用意します。
- [2]. データの標準化(後述)を行います。
- [3]. データの範囲内で、ランダムな位置にk個のクラスターを作成します。
- [4]. 各データを位置的にもっとも近い距離にあるクラスターに所属させます。
- [5]. 各クラスターの位置を、そのクラスターに属しているデータの平均の位置に移動させます。
- [6]. 設定したイテレーション数に達するか、もしくはクラスターの位置が変わらなくなるまで[4]~[5]の計算を繰り返します。
Pythonでの実装
前述の計算をPythonで書いてみて、可視化までやってみます。
使うもの
- Python 3.8.5
- matplotlib==3.3.2
- VS Code上のJupyter
※過去の記事と同様、勉強のためなるべくアルゴリズム部分はライブラリを使わずにPythonの標準モジュールを使って進めていきます。ただし、可視化などの目的でmatplotlibのみは今回利用します。
この記事では割愛するもの
本記事ではアルゴリズムの理解を深めることを目的とするため、シンプルになるように以下のものは扱いません。
- 2次元を超えるデータでのk平均法。
- k平均法を発展させたもの。
- 例 : 初期のクラスターの初期位置をより最適なものにしたり、kの個数が自動決定されるようなk-means++やx-meansなど。
- 細かいパフォーマンスの最適化はスキップします。
必要なモジュールのimportと初期設定
まずは必要なもののimportや可視化のためのmatplotlibのプロット設定などを行います。
from __future__ import annotations
from typing import List
from math import sqrt
from copy import deepcopy
from statistics import pstdev, mean
import random
from datetime import datetime
import matplotlib.pyplot as plt
import matplotlib
matplotlib.style.use('ggplot')
%matplotlib inline
annotationsはPython3.10からデフォルトとなる、一部の型アノテーション関係の挙動を有効化するためにimportしています。また、型アノテーションを利用して型チェックを行いつつ書き進めるため、typingモジュールのものを一部import1しています。
sqrt、pstdev、meanはそれぞれ平方根計算、標準偏差の計算、平均計算用の関数です。前者2つは標準化(standardize)の計算で利用し、平均はクラスターの位置更新時に利用します。
また、クラスターの更新が終わるまで過程の各イテレーションのクラスターを、過程の可視化目的で保持しようと思うため値のディープコピー用にdeepcopy関数をimportしています。
randomモジュールはランダムな座標の生成目的で一様分布用の関数(uniform)で使います。
あとは可視化用にmatplotlib関係のimportや設定を行っています。
座標用のクラスの定義
今回は2次元空間でのk平均法を進めていくので、横軸(X)と縦軸(Y)の値が扱えれば計算ができるので、XとYの属性を持つPointクラスを追加していきます。
class Point:
def __init__(self, x: float, y: float) -> None:
"""
特定の2次元空間の座標単体を扱うクラス。matplotlibに合わせて、
左下を(0, 0)とし、右上にいくごとにインクリメントする形の座標
空間で扱う。
Parameters
----------
x : float
X座標。
y : float
Y座標。
"""
self.x: float = x
self.y: float = y
k平均法の計算過程で、各座標がどのクラスターに一番近いのかの計算が必要になるので、他の座標とのユークリッド距離を取得できるメソッドを追加します。
参考 : 2次元ユークリッド距離の性質
計算としては1つ目のX座標を$x$, 2つ目のX座標を$x'$, 1つ目のY座標を$y$, 2つ目のY座標を$y'$, 求まる距離を$D$とすると、以下の計算式で対応ができます。懐かしの中学の数学で学ぶ計算ですね。
D = \sqrt{(x - x')^2 + (y - y')^2}
def distance(self, other_point: Point) -> float:
"""
引数に指定された座標間のユークリッド距離を取得する。
Parameters
----------
other_point : Point
対象の座標。
Returns
-------
distance_val : float
算出された2つの座標間のユークリッド距離の値。
"""
x1: float = self.x
x2: float = other_point.x
y1: float = self.y
y2: float = other_point.y
distance_val: float = sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
return distance_val
また、計算家計のイテレーションで各クラスターの座標がイテレーションで変動していないことの判定を行うために、__eq__メソッドを追加しPointクラス同士の比較ができる(XとYが一致していればTrueになる)ようにしておきます。
def __eq__(self, other: object) -> bool:
"""
他のPointのインスタンスと等値かどうかの比較を行う。
Parameters
----------
other : object
比較対象のインスタンス。もしPoint関係のインスタンスではない
場合には比較処理はスキップされる。
Returns
-------
is_equal : bool
等値かどうかの真偽値。座標の比較で処理される。
"""
if not isinstance(other, Point):
return NotImplemented
is_equal: bool = self.x == other.x and self.y == other.y
return is_equal
計算では1つ前の各クラスターと現在の各クラスターが一致していることを比較しますが、Pythonでは以下のようにリスト内に値を入れる形での比較でも計算することができるのでそちらを後々利用します。
>>> point_list_A: List[Point] = [Point(x=10, y=20)]
>>> point_list_B: List[Point] = [Point(x=10, y=20)]
>>> print(point_list_A == point_list_B)
True
クラスター用のクラスの定義
次はクラスター用のクラスを定義していきます。
こちらはシンプルで、centroidとpointsという2つの属性を持つだけのクラスとなります。
centroidは「重心」とか「質量中心」といった意味を持つ単語です。k平均法ではクラスターに属する座標の中心(平均)位置として使われます。イテレーションを繰り返す度に属する座標が変動するため、このcentroidの座標値も同様にイテレーションの度に変化します。
pointsの属性はこのクラスターに属する各座標を格納するためのリストです。
class Cluster:
def __init__(self, centroid: Point, points: List[Point]):
"""
1つ分のクラスターを扱うためのクラス。
Parameters
----------
centroid : Point
クラスターの中央位置となる座標情報。
points : list of Point
対象のクラスターに属している座標のリスト。
"""
self.centroid = centroid
self.points = points
k平均法のアルゴリズム用のクラスの定義
k平均法のアルゴリズム制御用のクラスを追加していきます。
コンストラクタの定義
コンストラクタではクラスター数としてのkとクラスタリング対象の座標群としてのpointsという2つの引数を受け付けるようにしています。
また、事前に各座標の標準化(後述)を行って各座標値を変換してしまう(_get_standardized_points部分)ので、元の座標を保持するために_original_pointsという属性を設けてあります。
その他、各クラスターの初期化(後述)もコンストラクタで行っています(_initialize_clusters部分)。
class KMeans:
def __init__(self, k: int, points: List[Point]) -> None:
"""
KMeansのアルゴリズム制御用のクラス。
Parameters
----------
k : int
設定するクラスター数。
points : list of Point
対象とする座標のリスト。
"""
self._original_points = points
self._k = k
self._standardized_points: List[Point] = self._get_standardized_points()
self._initialize_clusters()
各座標を標準化する
今回扱うケースではそこまで大きな差ではありませんが、通常は次元(軸)によって数値のスケールが大きく異なる場合があります。たとえば横軸が年齢、縦軸が売り上げといった2次元のデータを扱うケースを考えると、横軸の数値は縦軸の数値と比べると大分小さくなってしまいがちでクラスタリングで扱うには不適切です。
そのため今回の記事でも標準化(standardized)の処理を各座標に対して入れていきます。機械学習方面でもライブラリでよくScaler(例 : StandardScaler, MinMaxScalerなど)や正規化(normalization)などの変換処理の単語が出てきますが、そういった感じの前処理の変換となります。
今回はZ値(z-score)と呼ばれる標準化の処理を入れていきます。
z-scoreの概要と計算方法
z-scoreは、値(今回は座標)が平均値から標準偏差の何個分離れているのかという値になります。z-scoreを$Z$とすると式で表すと以下のようになります。
Z = (座標値 - 平均値) ÷ 標準偏差
これをX軸とY軸の座標値に反映することで、縦と横のスケールが合うようになります。
z-score反映用のメソッドの定義
KMeansクラスにz-score用の各メソッドを追加していきます。
まずは元の座標とは別にしたいため、deepcopy(self._original_points)という記述部分で各座標のディープコピーを作っています。
コピーしたものに対して、X軸とY軸の各座標値にそれぞれ標準化の処理を反映しています。
前節で触れたz-scoreの計算は_apply_z_scoreメソッド内で記述しています。平均はmean関数、標準辺さはpstdev関数で取っています。
def _get_standardized_points(self) -> List[Point]:
"""
標準化された座標のリストを取得する。
Notes
-----
標準化にはz-scoreの計算が使われる。
Returns
-------
standardized_points : list of Point
標準化後の各座標を格納したリスト。
"""
standardized_points: List[Point] = deepcopy(self._original_points)
self._standardize_x(points=standardized_points)
self._standardize_y(points=standardized_points)
return standardized_points
def _standardize_x(self, points: List[Point]) -> None:
"""
指定された座標のリストのX座標の標準化を行う。
Parameters
----------
points : list of Point
変換対象の座標のリスト。
"""
x_list: List[float] = [point.x for point in points]
x_list = self._apply_z_score(list_val=x_list)
for i, point in enumerate(points):
point.x = x_list[i]
def _standardize_y(self, points: List[Point]) -> None:
"""
指定された座標のリストのY座標の標準化を行う。
Parameters
----------
points : list of Point
変換対象の座標のリスト。
"""
y_list: List[float] = [point.y for point in points]
y_list = self._apply_z_score(list_val=y_list)
for i, point in enumerate(points):
point.y = y_list[i]
def _apply_z_score(self, list_val: List[float]) -> List[float]:
"""
指定された座標値を格納したリストにz-scoreの標準化を反映する。
Parameters
----------
list_val : list of float
座標値を格納したリスト。
Returns
-------
list_val : list of float
z-score反映後の座標値のリスト。
"""
mean_val: float = mean(list_val)
std_val: float = pstdev(list_val)
for i, coordinate in enumerate(list_val):
standardized_val: float = (coordinate - mean_val) / std_val
list_val[i] = standardized_val
return list_val
クラスターの初期化を行う
引き続きコンストラクタで必要な処理(コンストラクタで呼び出されているメソッド)の追加を進めていきます。今度はクラスターの初期化です。
やることとしては、
- コンストラクタに指定されたk(クラスター数)分のClusterインスタンスを生成してリストに追加。
- 各クラスターのcentroid(クラスターの重心点)の値(初期値)は、標準化された座標の最小~最大値の範囲内でランダムに決定する。
- クラスターに属する各座標はまだこの時点では無し(空のリスト)で生成する。
といった処理になります。
def _initialize_clusters(self) -> None:
"""
クラスターの初期化を行う。クラスター中心点(centroid)は
ランダムな位置が設定され、属する座標点は空の状態でリストが
生成される。
"""
self._clusters: List[Cluster] = []
for _ in range(self._k):
random_point: Point = self._get_standardized_random_point()
cluster: Cluster = Cluster(
centroid=random_point,
points=[])
self._clusters.append(cluster)
def _get_standardized_random_point(self) -> Point:
"""
ランダムな座標点を生成・取得する。
Returns
-------
random_point : Point
生成された座標点。
"""
x_min: float = self._get_standardized_x_min()
x_max: float = self._get_standardized_x_max()
y_min: float = self._get_standardized_y_min()
y_max: float = self._get_standardized_y_max()
random_x: float = random.uniform(a=x_min, b=x_max)
random_y: float = random.uniform(a=y_min, b=y_max)
random_point: Point = Point(x=random_x, y=random_y)
return random_point
def _get_standardized_x_max(self) -> float:
"""
標準化された座標値の中でのX座標の最大値を取得する。
Returns
-------
x_max : float
X座標の最大値。
"""
x_list: List[float] = self._get_standardized_x_list()
x_max: float = max(x_list)
return x_max
def _get_standardized_x_min(self) -> float:
"""
標準化された座標値の中でのX座標の最小値を取得する。
Parameters
----------
x_min : float
X座標の最小値。
"""
x_list: List[float] = self._get_standardized_x_list()
x_min: float = min(x_list)
return x_min
def _get_standardized_x_list(self) -> List[float]:
"""
存在する標準化された座標値(クラスターの中心座標を除く)のX座標の
リストを取得する。
Returns
-------
x_list : list of float
X座標のリスト。
"""
x_list: List[float] = [point.x for point in self._standardized_points]
return x_list
def _get_standardized_y_max(self) -> float:
"""
標準化された座標値の中でのY座標の最大値を取得する。
Returns
-------
y_max : float
Y座標の最大値。
"""
y_list: List[float] = self._get_standardized_y_list()
y_max: float = max(y_list)
return y_max
def _get_standardized_y_min(self) -> float:
"""
標準化された座標値の中でのY座標の最小値を取得する。
Returns
-------
y_min : float
Y座標の最小値。
"""
y_list: List[float] = self._get_standardized_y_list()
y_min: float = min(y_list)
return y_min
def _get_standardized_y_list(self) -> List[float]:
"""
存在する標準化された座標値(クラスターの中心座標を除く)のY座標の
リストを取得する。
Returns
-------
y_list : list of float
Y座標のリスト。
"""
y_list: List[float] = [point.y for point in self._standardized_points]
return y_list
各座標をいずれかのクラスターに所属させるための処理の実装
ここからはコンストラクタではなく、k平均法を動かした際の各イテレーションで利用する処理を書いていきます。
k平均法の計算で、各イテレーションで「各座標をいずれかのクラスターに所属させる」「各クラスターの中央(重心)点を更新する」といった計算が繰り返し必要になりますが、そのうちの各座標をクラスターに所属させる部分を書いていきます。
処理としては、
- 各クラスターに所属している座標のリストを一旦リセット(空に)する。
- 各座標を(ユークリッド距離で)一番近いクラスターに所属(クラスターのpointsのリストに追加)させる。
といった処理になります。
def _assign_points_to_cluster(self) -> None:
"""
各座標を一番近いクラスターへ割り当てる(クラスターの座標のリストへ
各座標を追加する)。
Notes
-----
実行時点での割り当てられている座標は最初にリセットされる。
"""
self._reset_clusters_assignment()
for standardized_point in self._standardized_points:
nearest_cluster: Cluster = self._get_target_point_nearest_cluster(
standardized_point=standardized_point)
nearest_cluster.points.append(standardized_point)
def _reset_clusters_assignment(self) -> None:
"""
各クラスターへの座標の割り当てをリセット(空に)する。
"""
for cluster in self._clusters:
cluster.points.clear()
def _get_target_point_nearest_cluster(
self, standardized_point: Point) -> Cluster:
"""
対象の座標に対して一番近いクラスターを取得する。
Parameters
----------
standardized_point : Point
対象の標準化された座標。
Returns
-------
nearest_cluster : Cluster
対象の座標に一番近いクラスター。
"""
min_distance: float = self._clusters[0].centroid.distance(
other_point=standardized_point)
nearest_cluster: Cluster = self._clusters[0]
for cluster in self._clusters:
distance: float = cluster.centroid.distance(
other_point=standardized_point)
if distance >= min_distance:
continue
min_distance = distance
nearest_cluster = cluster
return nearest_cluster
各クラスターの中心(重心)点の更新処理の実装
こちらも各イテレーションで利用するメソッドです。
各座標の最も近いクラスターへの所属が終わったタイミングで、クラスターに所属している各座標の平均を取って、その平均の座標をクラスターの中心(重心)点(centroid)に設定します。
計算自体はmean関数を使ったシンプルなものになります。
def _update_cluster_centroid(self) -> None:
"""
クラスターに属している座標のリストを参照して、各クラスターの
中央座標(各座標の平均値)を更新する。
"""
for cluster in self._clusters:
if not cluster.points:
continue
x_list: List[float] = [point.x for point in cluster.points]
y_list: List[float] = [point.y for point in cluster.points]
mean_x: float = mean(x_list)
mean_y: float = mean(y_list)
cluster.centroid.x = mean_x
cluster.centroid.y = mean_y
アルゴリズムのイテレーションのためのメソッドの実装
前セクションまでに用意した、「各座標を一番近いクラスターに所属させる」処理と「各クラスターの中心(重心)点を更新する」処理をループで繰り替えし実行する処理を追加します。
各イテレーションでクラスターがどんな感じに変化していっているのかを後々確認(可視化)するため、イテレーションごとにクラスターのリストをコピーし、イテレーションが終わったらクラスターのヒストリーとしてそのデータを返却しています。
def run_algorithm(self, max_iterations: int=100) -> List[List[Cluster]]:
"""
k-meansのアルゴリズムを実行する。
Parameters
----------
max_iterations : int
イテレーションの最大数。
Returns
-------
clusters_history : list of list
各イテレーションにおける、クラスター群を格納する多次元のリスト。
1次元目は各イテレーション、2次元目はそのイテレーションにおける
一通りのクラスターを格納する。
"""
clusters_history: List[List[Cluster]] = []
for iteration in range(max_iterations):
if iteration % 10 == 0:
print(
datetime.now(),
'イテレーション%sの計算を開始...' % iteration)
self._assign_points_to_cluster()
previous_clusters: List[Cluster] = deepcopy(self._clusters)
self._update_cluster_centroid()
if self._clusters == previous_clusters:
print('クラスターが変動しなくなったため処理を停止します。')
break
clusters_history.append(deepcopy(self._clusters))
return clusters_history
可視化用のメソッドの追加
今回はX座標とY座標の2次元空間なので可視化が容易にできるのでそのためのメソッドを追加していきます。
。
元々の座標と各イテレーションでのクラスター群の可視化の2つのメソッドを追加します。
各クラスターの方ではクラスターごとの所属座標を色を分けて、且つクラスターの中心(重心)点を★でプロットしています(marker='*'の指定で★の表示になります)。
def plot_original_points(self) -> None:
"""
標準化前の各座標のプロットを行う。
Parameters
----------
points : list of Point
各座標を格納したリスト。
"""
x_list = [point.x for point in self._original_points]
y_list = [point.y for point in self._original_points]
plt.figure(figsize=(6, 6))
plt.scatter(x_list, y_list)
def plot_clusters(self, clusters: List[Cluster]) -> None:
"""
各クラスターの中心座標と属している各座標のプロットを行う。
Parameters
----------
clusters : list of Cluster
プロット対象のクラスターのリスト。
"""
plt.figure(figsize=(6, 6))
for cluster in clusters:
x_list: List[float] = [point.x for point in cluster.points]
y_list: List[float] = [point.y for point in cluster.points]
plt.scatter(x_list, y_list)
centroid_x: float = cluster.centroid.x
centroid_y: float = cluster.centroid.y
plt.scatter([centroid_x], [centroid_y], marker='*', s=200)
ランダムな座標を生成するヘルパーを追加
アルゴリズムを動かすために、ランダムな座標を生成・リストに追加する関数を追加しておきます。
def _append_random_point_to_list(
num: int, x_min: float, x_max: float,
y_min: float, y_max: float, points: List[Point]) -> None:
"""
座標のリストへ、指定された件数分ランダムに生成された座標を
追加する。
Parameters
----------
num : int
リストに追加する座標数。
x_min : float
ランダムな座標範囲のX座標の最小値。
x_max : float
ランダムな座標範囲のX座標の最大値。
y_min : float
ランダムな座標範囲のY座標の最小値。
y_max : float
ランダムな座標範囲のY座標の最大値。
points : list of Point
追加先となるリスト。
"""
for _ in range(num):
random_x = random.uniform(a=x_min, b=x_max)
random_y = random.uniform(a=y_min, b=y_max)
point: point = Point(x=random_x, y=random_y)
points.append(point)
アルゴリズムを動かす
諸々の準備ができたのでアルゴリズムを動かしていきます。
今回はある程度ランダムな範囲を被らせつつ、3つの設定で初期座標を生成しました。
points: List[Point] = []
_append_random_point_to_list(
num=50, x_min=0, x_max=400, y_min=0, y_max=500, points=points)
_append_random_point_to_list(
num=100, x_min=200, x_max=400, y_min=300, y_max=500, points=points)
_append_random_point_to_list(
num=70, x_min=300, x_max=500, y_min=400, y_max=700, points=points)
kmeans = KMeans(k=3, points=points)
clusters_history: List[List[Cluster]] = kmeans.run_algorithm()
2020-11-07 16:02:58.607707 イテレーション0の計算を開始...
2020-11-07 16:02:58.660701 イテレーション10の計算を開始...
2020-11-07 16:02:58.723702 イテレーション20の計算を開始...
2020-11-07 16:02:58.772699 イテレーション30の計算を開始...
2020-11-07 16:02:58.826700 イテレーション40の計算を開始...
2020-11-07 16:02:58.875700 イテレーション50の計算を開始...
2020-11-07 16:02:58.922701 イテレーション60の計算を開始...
2020-11-07 16:02:58.968699 イテレーション70の計算を開始...
2020-11-07 16:02:59.017699 イテレーション80の計算を開始...
2020-11-07 16:02:59.068731 イテレーション90の計算を開始...
可視化してみる
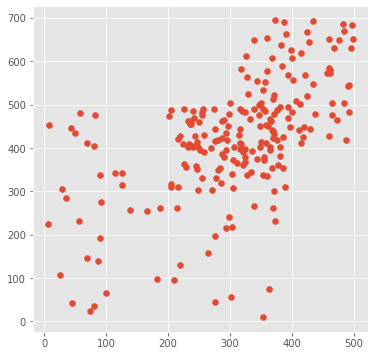
まずは元のランダムな座標(_append_random_point_to_list関数で生成された座標)をプロットしてみます。
kmeans.plot_original_points()
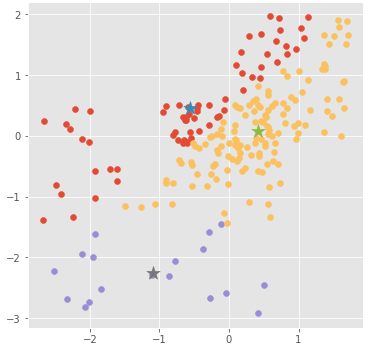
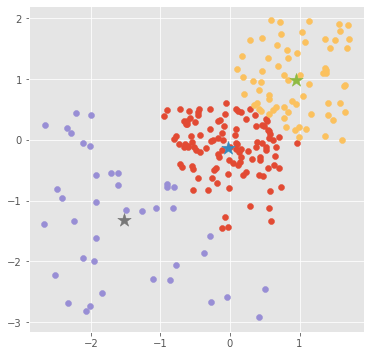
続いて各イテレーションでのアルゴリズム反映後のものを見ていきます。イテレーション数が少ない段階だとまだ微妙な感じのクラスタリングになります。また、軸の値も標準化された後の値になります。
イテレーション : 0
kmeans.plot_clusters(clusters=clusters_history[0])
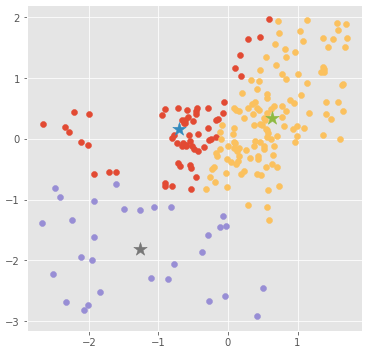
イテレーション : 1
kmeans.plot_clusters(clusters=clusters_history[1])
イテレーション : 2
kmeans.plot_clusters(clusters=clusters_history[2])
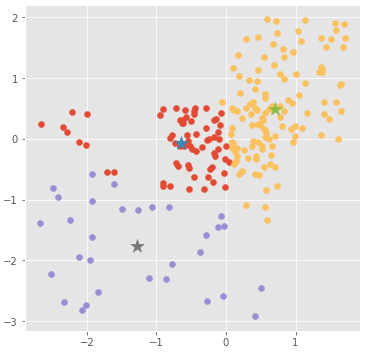
最後のイテレーション(イテレーション99)
kmeans.plot_clusters(
clusters=clusters_history[len(clusters_history) - 1])
それっぽく動いていそうです。無事クラスタリングを行うことができました。
コード全体
from __future__ import annotations
from typing import List
from math import sqrt
from copy import deepcopy
from statistics import pstdev, mean
import random
from datetime import datetime
import matplotlib.pyplot as plt
import matplotlib
matplotlib.style.use('ggplot')
%matplotlib inline
class Point:
def __init__(self, x: float, y: float) -> None:
"""
特定の2次元空間の座標単体を扱うクラス。matplotlibに合わせて、
左下を(0, 0)とし、右上にいくごとにインクリメントする形の座標
空間で扱う。
Parameters
----------
x : float
X座標。
y : float
Y座標。
"""
self.x: float = x
self.y: float = y
def distance(self, other_point: Point) -> float:
"""
引数に指定された座標間のユークリッド距離を取得する。
Parameters
----------
other_point : Point
対象の座標。
Returns
-------
distance_val : float
算出された2つの座標間のユークリッド距離の値。
"""
x1: float = self.x
x2: float = other_point.x
y1: float = self.y
y2: float = other_point.y
distance_val: float = sqrt((x1 - x2) ** 2 + (y1 - y2) ** 2)
return distance_val
def __eq__(self, other: object) -> bool:
"""
他のPointのインスタンスと等値かどうかの比較を行う。
Parameters
----------
other : object
比較対象のインスタンス。もしPoint関係のインスタンスではない
場合には比較処理はスキップされる。
Returns
-------
is_equal : bool
等値かどうかの真偽値。座標の比較で処理される。
"""
if not isinstance(other, Point):
return NotImplemented
is_equal: bool = self.x == other.x and self.y == other.y
return is_equal
class Cluster:
def __init__(self, centroid: Point, points: List[Point]):
"""
1つ分のクラスターを扱うためのクラス。
Parameters
----------
centroid : Point
クラスターの中央位置となる座標情報。
points : list of Point
対象のクラスターに属している座標のリスト。
"""
self.centroid = centroid
self.points = points
class KMeans:
def __init__(self, k: int, points: List[Point]) -> None:
"""
KMeansのアルゴリズム制御用のクラス。
Parameters
----------
k : int
設定するクラスター数。
points : list of Point
対象とする座標のリスト。
"""
self._original_points = points
self._k = k
self._standardized_points: List[Point] = self._get_standardized_points()
self._initialize_clusters()
def _get_standardized_points(self) -> List[Point]:
"""
標準化された座標のリストを取得する。
Notes
-----
標準化にはz-scoreの計算が使われる。
Returns
-------
standardized_points : list of Point
標準化後の各座標を格納したリスト。
"""
standardized_points: List[Point] = deepcopy(self._original_points)
self._standardize_x(points=standardized_points)
self._standardize_y(points=standardized_points)
return standardized_points
def _standardize_x(self, points: List[Point]) -> None:
"""
指定された座標のリストのX座標の標準化を行う。
Parameters
----------
points : list of Point
変換対象の座標のリスト。
"""
x_list: List[float] = [point.x for point in points]
x_list = self._apply_z_score(list_val=x_list)
for i, point in enumerate(points):
point.x = x_list[i]
def _standardize_y(self, points: List[Point]) -> None:
"""
指定された座標のリストのY座標の標準化を行う。
Parameters
----------
points : list of Point
変換対象の座標のリスト。
"""
y_list: List[float] = [point.y for point in points]
y_list = self._apply_z_score(list_val=y_list)
for i, point in enumerate(points):
point.y = y_list[i]
def _apply_z_score(self, list_val: List[float]) -> List[float]:
"""
指定された座標値を格納したリストにz-scoreの標準化を反映する。
Parameters
----------
list_val : list of float
座標値を格納したリスト。
Returns
-------
list_val : list of float
z-score反映後の座標値のリスト。
"""
mean_val: float = mean(list_val)
std_val: float = pstdev(list_val)
for i, coordinate in enumerate(list_val):
standardized_val: float = (coordinate - mean_val) / std_val
list_val[i] = standardized_val
return list_val
def _initialize_clusters(self) -> None:
"""
クラスターの初期化を行う。クラスター中心点(centroid)は
ランダムな位置が設定され、属する座標点は空の状態でリストが
生成される。
"""
self._clusters: List[Cluster] = []
for _ in range(self._k):
random_point: Point = self._get_standardized_random_point()
cluster: Cluster = Cluster(
centroid=random_point,
points=[])
self._clusters.append(cluster)
def _get_standardized_random_point(self) -> Point:
"""
ランダムな座標点を生成・取得する。
Returns
-------
random_point : Point
生成された座標点。
"""
x_min: float = self._get_standardized_x_min()
x_max: float = self._get_standardized_x_max()
y_min: float = self._get_standardized_y_min()
y_max: float = self._get_standardized_y_max()
random_x: float = random.uniform(a=x_min, b=x_max)
random_y: float = random.uniform(a=y_min, b=y_max)
random_point: Point = Point(x=random_x, y=random_y)
return random_point
def _get_standardized_x_max(self) -> float:
"""
標準化された座標値の中でのX座標の最大値を取得する。
Returns
-------
x_max : float
X座標の最大値。
"""
x_list: List[float] = self._get_standardized_x_list()
x_max: float = max(x_list)
return x_max
def _get_standardized_x_min(self) -> float:
"""
標準化された座標値の中でのX座標の最小値を取得する。
Parameters
----------
x_min : float
X座標の最小値。
"""
x_list: List[float] = self._get_standardized_x_list()
x_min: float = min(x_list)
return x_min
def _get_standardized_x_list(self) -> List[float]:
"""
存在する標準化された座標値(クラスターの中心座標を除く)のX座標の
リストを取得する。
Returns
-------
x_list : list of float
X座標のリスト。
"""
x_list: List[float] = [point.x for point in self._standardized_points]
return x_list
def _get_standardized_y_max(self) -> float:
"""
標準化された座標値の中でのY座標の最大値を取得する。
Returns
-------
y_max : float
Y座標の最大値。
"""
y_list: List[float] = self._get_standardized_y_list()
y_max: float = max(y_list)
return y_max
def _get_standardized_y_min(self) -> float:
"""
標準化された座標値の中でのY座標の最小値を取得する。
Returns
-------
y_min : float
Y座標の最小値。
"""
y_list: List[float] = self._get_standardized_y_list()
y_min: float = min(y_list)
return y_min
def _get_standardized_y_list(self) -> List[float]:
"""
存在する標準化された座標値(クラスターの中心座標を除く)のY座標の
リストを取得する。
Returns
-------
y_list : list of float
Y座標のリスト。
"""
y_list: List[float] = [point.y for point in self._standardized_points]
return y_list
def _assign_points_to_cluster(self) -> None:
"""
各座標を一番近いクラスターへ割り当てる(クラスターの座標のリストへ
各座標を追加する)。
Notes
-----
実行時点での割り当てられている座標は最初にリセットされる。
"""
self._reset_clusters_assignment()
for standardized_point in self._standardized_points:
nearest_cluster: Cluster = self._get_target_point_nearest_cluster(
standardized_point=standardized_point)
nearest_cluster.points.append(standardized_point)
def _reset_clusters_assignment(self) -> None:
"""
各クラスターへの座標の割り当てをリセット(空に)する。
"""
for cluster in self._clusters:
cluster.points.clear()
def _get_target_point_nearest_cluster(
self, standardized_point: Point) -> Cluster:
"""
対象の座標に対して一番近いクラスターを取得する。
Parameters
----------
standardized_point : Point
対象の標準化された座標。
Returns
-------
nearest_cluster : Cluster
対象の座標に一番近いクラスター。
"""
min_distance: float = self._clusters[0].centroid.distance(
other_point=standardized_point)
nearest_cluster: Cluster = self._clusters[0]
for cluster in self._clusters:
distance: float = cluster.centroid.distance(
other_point=standardized_point)
if distance >= min_distance:
continue
min_distance = distance
nearest_cluster = cluster
return nearest_cluster
def _update_cluster_centroid(self) -> None:
"""
クラスターに属している座標のリストを参照して、各クラスターの
中央座標(各座標の平均値)を更新する。
"""
for cluster in self._clusters:
if not cluster.points:
continue
x_list: List[float] = [point.x for point in cluster.points]
y_list: List[float] = [point.y for point in cluster.points]
mean_x: float = mean(x_list)
mean_y: float = mean(y_list)
cluster.centroid.x = mean_x
cluster.centroid.y = mean_y
def run_algorithm(self, max_iterations: int=100) -> List[List[Cluster]]:
"""
k-meansのアルゴリズムを実行する。
Parameters
----------
max_iterations : int
イテレーションの最大数。
Returns
-------
clusters_history : list of list
各イテレーションにおける、クラスター群を格納する多次元のリスト。
1次元目は各イテレーション、2次元目はそのイテレーションにおける
一通りのクラスターを格納する。
"""
clusters_history: List[List[Cluster]] = []
for iteration in range(max_iterations):
if iteration % 10 == 0:
print(
datetime.now(),
'イテレーション%sの計算を開始...' % iteration)
self._assign_points_to_cluster()
previous_clusters: List[Cluster] = deepcopy(self._clusters)
self._update_cluster_centroid()
if self._clusters == previous_clusters:
print('クラスターが変動しなくなったため処理を停止します。')
break
clusters_history.append(deepcopy(self._clusters))
return clusters_history
def plot_original_points(self) -> None:
"""
標準化前の各座標のプロットを行う。
Parameters
----------
points : list of Point
各座標を格納したリスト。
"""
x_list = [point.x for point in self._original_points]
y_list = [point.y for point in self._original_points]
plt.figure(figsize=(6, 6))
plt.scatter(x_list, y_list)
def plot_clusters(self, clusters: List[Cluster]) -> None:
"""
各クラスターの中心座標と属している各座標のプロットを行う。
Parameters
----------
clusters : list of Cluster
プロット対象のクラスターのリスト。
"""
plt.figure(figsize=(6, 6))
for cluster in clusters:
x_list: List[float] = [point.x for point in cluster.points]
y_list: List[float] = [point.y for point in cluster.points]
plt.scatter(x_list, y_list)
centroid_x: float = cluster.centroid.x
centroid_y: float = cluster.centroid.y
plt.scatter([centroid_x], [centroid_y], marker='*', s=200)
def _append_random_point_to_list(
num: int, x_min: float, x_max: float,
y_min: float, y_max: float, points: List[Point]) -> None:
"""
座標のリストへ、指定された件数分ランダムに生成された座標を
追加する。
Parameters
----------
num : int
リストに追加する座標数。
x_min : float
ランダムな座標範囲のX座標の最小値。
x_max : float
ランダムな座標範囲のX座標の最大値。
y_min : float
ランダムな座標範囲のY座標の最小値。
y_max : float
ランダムな座標範囲のY座標の最大値。
points : list of Point
追加先となるリスト。
"""
for _ in range(num):
random_x = random.uniform(a=x_min, b=x_max)
random_y = random.uniform(a=y_min, b=y_max)
point: point = Point(x=random_x, y=random_y)
points.append(point)
points: List[Point] = []
_append_random_point_to_list(
num=50, x_min=0, x_max=400, y_min=0, y_max=500, points=points)
_append_random_point_to_list(
num=100, x_min=200, x_max=400, y_min=300, y_max=500, points=points)
_append_random_point_to_list(
num=70, x_min=300, x_max=500, y_min=400, y_max=700, points=points)
kmeans = KMeans(k=3, points=points)
clusters_history: List[List[Cluster]] = kmeans.run_algorithm()
kmeans.plot_original_points()
kmeans.plot_clusters(clusters=clusters_history[0])
kmeans.plot_clusters(clusters=clusters_history[1])
kmeans.plot_clusters(clusters=clusters_history[2])