はじめに
以前k-meansに関する記事を投稿しました。
k-meansは初期値依存という問題を抱えているため、その克服を目指したk-means++というアルゴリズムが開発されています。
今回はk-means++について勉強した内容をまとめました。
参考
k-means++の理解に当たって下記を参考にさせていただきました。
- 言語処理のための機械学習入門 (自然言語処理シリーズ) 高村 大也 (著), 奥村 学 (監修) 出版社; コロナ社
- 機械学習のエッセンス 加藤公一(著) 出版社; SBクリエイティブ株式会社
- k-means++法 - Wikipedia
k-means++について
k-meansの復習
k-meansの概要
k-meansは、まずデータを適当なクラスタに分けた後、クラスタの平均を用いてうまい具合にデータがわかれるように調整させていくアルゴリズムです。任意の指定のk個のクラスタを作成するアルゴリズムであることから、k-means法(k点平均法)と呼ばれています。
k-meansのアルゴリズム
k-meansは具体的には下記のような工程を辿ります。
- 各点$x_{i}$に対してランダムにクラスタを割り振る
- 各クラスタに割り当てられた点について重心を計算する
- 各点について上記で計算された重心からの距離を計算し、距離が一番近いクラスタに割り当て直す。
- 2.と3.の工程を、割り当てられるクラスタが変化しなくなるまで行う
k-meansの問題点
k-meansは最初にランダムにクラスタを割り振るため、その初期値によって最適とはかけ離れたクラスタリングがなされてしまう可能性があります。また、これも初期値によって結果が収束するまでの時間も多く要します。
k-means++
k-means++の概要
k-means++は上記の初期値依存問題の克服を目指したアルゴリズムです。
k-means++は初期のクラスタの中心同士は離れていた方がよいという考え方に基づいて設計されており、初期のクラスタの割り振りはデータポイント間の距離に応じて確率的には割り振ります。
k-means++のアルゴリズム
- 各点$x_{i}$の中からランダムに1点を選び、クラスタの中心とする
- 各点$x_{i}$に関して、既存のクラスタ中心の中から最も近いクラスタ中心との距離$D(x)$を計算する
- 各点$x_{i}$に関して重み付き確率分布$\frac{D(x)^2}{\sum_{} D(x)^2}$を用いて、新しいクラスタ中心をランダムに選ぶ
- 2.と3.の工程をk個のクラスタ中心が選定できるまで行う
上記のように初期のクラスタ中心点をデータ点間の距離に基づいて確率的に決定することで、初期値依存問題の解決を試みています。
k-means++を実装する
ライブラリを用いないk-means++の実装
ライブラリを用いずk-means法を実装したものが下記になります。
機械学習のエッセンス記載のk-meansのコードをベースとし、k-means++に変更するにあたって自分で修正を加えています。
import numpy as np
class KMeans_pp:
def __init__(self, n_clusters, max_iter = 1000, random_seed = 0):
self.n_clusters = n_clusters
self.max_iter = max_iter
self.random_state = np.random.RandomState(random_seed)
def fit(self, X):
#ランダムに最初のクラスタ点を決定
tmp = np.random.choice(np.array(range(X.shape[0])))
first_cluster = X[tmp]
first_cluster = first_cluster[np.newaxis,:]
#最初のクラスタ点とそれ以外のデータ点との距離の2乗を計算し、それぞれをその総和で割る
p = ((X - first_cluster)**2).sum(axis = 1) / ((X - first_cluster)**2).sum()
r = np.random.choice(np.array(range(X.shape[0])), size = 1, replace = False, p = p)
first_cluster = np.r_[first_cluster ,X[r]]
#分割するクラスター数が3個以上の場合
if self.n_clusters >= 3:
#指定の数のクラスタ点を指定できるまで繰り返し
while first_cluster.shape[0] < self.n_clusters:
#各クラスター点と各データポイントとの距離の2乗を算出
dist_f = ((X[:, :, np.newaxis] - first_cluster.T[np.newaxis, :, :])**2).sum(axis = 1)
#最も距離の近いクラスター点はどれか導出
f_argmin = dist_f.argmin(axis = 1)
#最も距離の近いクラスター点と各データポイントとの距離の2乗を導出
for i in range(dist_f.shape[1]):
dist_f.T[i][f_argmin != i] = 0
#新しいクラスタ点を確率的に導出
pp = dist_f.sum(axis = 1) / dist_f.sum()
rr = np.random.choice(np.array(range(X.shape[0])), size = 1, replace = False, p = pp)
#新しいクラスター点を初期値として加える
first_cluster = np.r_[first_cluster ,X[rr]]
#最初のラベルづけを行う
dist = (((X[:, :, np.newaxis] - first_cluster.T[np.newaxis, :, :]) ** 2).sum(axis = 1))
self.labels_ = dist.argmin(axis = 1)
labels_prev = np.zeros(X.shape[0])
count = 0
self.cluster_centers_ = np.zeros((self.n_clusters, X.shape[1]))
#各データポイントが属しているクラスターが変化しなくなった、又は一定回数の繰り返しを越した場合は終了
while (not (self.labels_ == labels_prev).all() and count < self.max_iter):
#その時点での各クラスターの重心を計算する
for i in range(self.n_clusters):
XX = X[self.labels_ == i, :]
self.cluster_centers_[i, :] = XX.mean(axis = 0)
#各データポイントと各クラスターの重心間の距離を総当たりで計算する
dist = ((X[:, :, np.newaxis] - self.cluster_centers_.T[np.newaxis, :, :]) ** 2).sum(axis = 1)
#1つ前のクラスターラベルを覚えておく。1つ前のラベルとラベルが変化しなければプログラムは終了する。
labels_prev = self.labels_
#再計算した結果、最も距離の近いクラスターのラベルを割り振る
self.labels_ = dist.argmin(axis = 1)
count += 1
self.count = count
def predict(self, X):
dist = ((X[:, :, np.newaxis] - self.cluster_centers_.T[np.newaxis, :, :]) ** 2).sum(axis = 1)
labels = dist.argmin(axis = 1)
return labels
検証
このアルゴリズムで本当にクラスタリングができているか検証したものが下記になります。
import matplotlib.pyplot as plt
# 適当なデータセットを作成する
np.random.seed(0)
points1 = np.random.randn(80, 2)
points2 = np.random.randn(80, 2) + np.array([4,0])
points3 = np.random.randn(80, 2) + np.array([5,8])
points = np.r_[points1, points2, points3]
np.random.shuffle(points)
# 3つのクラスタに分けるモデルを作成
model = KMeans_pp(3)
model.fit(points)
print(model.labels_)
すると出力はこのような感じになります。
見事3つにラベルが振られていることがわかります。
[2 1 0 2 1 1 0 1 2 0 1 1 0 1 0 0 1 1 0 2 0 1 2 0 1 2 0 2 1 2 1 1 1 0 1 0 1
2 2 1 1 1 1 2 0 1 1 1 0 2 1 0 2 1 0 1 0 2 2 2 2 2 1 0 1 0 0 1 1 1 1 1 0 1
0 0 0 2 1 0 2 0 1 1 0 1 2 0 2 2 2 0 0 0 2 0 0 0 2 0 2 1 1 1 1 1 0 1 2 1 2
0 1 2 2 1 2 0 2 2 2 0 0 2 0 2 1 2 2 0 1 2 1 2 2 2 1 0 2 1 1 2 0 0 0 2 1 1
1 0 0 0 1 1 2 0 1 0 0 0 2 0 0 0 0 0 2 2 1 2 0 2 2 0 1 2 2 2 2 1 0 2 1 2 2
0 2 0 0 0 2 0 1 2 0 0 0 1 1 1 1 2 2 0 2 2 2 0 0 1 1 2 2 0 1 1 2 1 2 2 0 2
1 2 0 2 1 2 0 0 2 2 0 2 0 2 1 2 2 0]
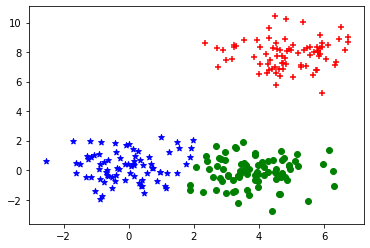
こちらをmatplotlibで図示してみます。
markers = ["+", "*", "o", '+']
color = ['r', 'b', 'g', 'k']
for i in range(4):
p = points[model.labels_ == i, :]
plt.scatter(p[:, 0], p[:, 1], marker = markers[i], color = color[i])
plt.show()
出力がこちら。概ね問題なくクラスタリングができていることがわかります。
また、クラスタリングが収束するまでの試行回数も出力してみます。
print(model.count)
4
今回k-means++のクラスタリングが収束するまでの試行回数は4回でした。普通のk-meansでも同様に試行回数をカウントすると、3回という結果でした。
本来であればk-means++の方が収束までの時間は短いとされているのでこのあたりはもう少し自分で検証したいと思います。
Next
混合正規分布によるクラスタリングやEMアルゴリズムによるクラスタリングにも挑戦していきたいと思います。