はじめに
機械学習において、ある任意の評価関数の値が最も良い値になるように、パラメターやモデルを調整することを最適化といいます。このページでは、最適化手法の中でも、機械学習(特にニューラルネットワーク)で最もよく使われる「勾配法」について紹介します。
Batch Gradient Descent (最急勾配法)
勾配法は一般的に下の式で表すことができます。$\theta$を最適化したいパラメター、Jを損失関数、μ を学習率とします。
\theta:=\theta-\theta \frac{\delta}{\delta \theta} J(\theta)
最急勾配法では、損失 J を以下の式で計算します。m 個のサンプル全ての損失を合計しているのが特徴です。パラメターをアップデートする度に、全サンプルの損失を計算しなくてはならないので、計算時間が大きく、メモリの使用量も相対的に大きいです。
J(\theta)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2}
Stochastic Gradient Descent(確率的勾配降下法)
確率的勾配降下法 SGDでは、ランダムに選ばれたサンプルを使って勾配を計算し、パラメター $\theta$をアップデートしていきます。SGDは最急勾配法に比べて、計算量とメモリの使用量も少ないですが、下のグラフを見ていただくとわかるように、最適値に収束するまでに上下の振れが見られます。
\theta=\theta-\eta \cdot \frac{\delta}{\delta \theta} J\left(\theta ; x^{(i)} ; y^{(i)}\right)
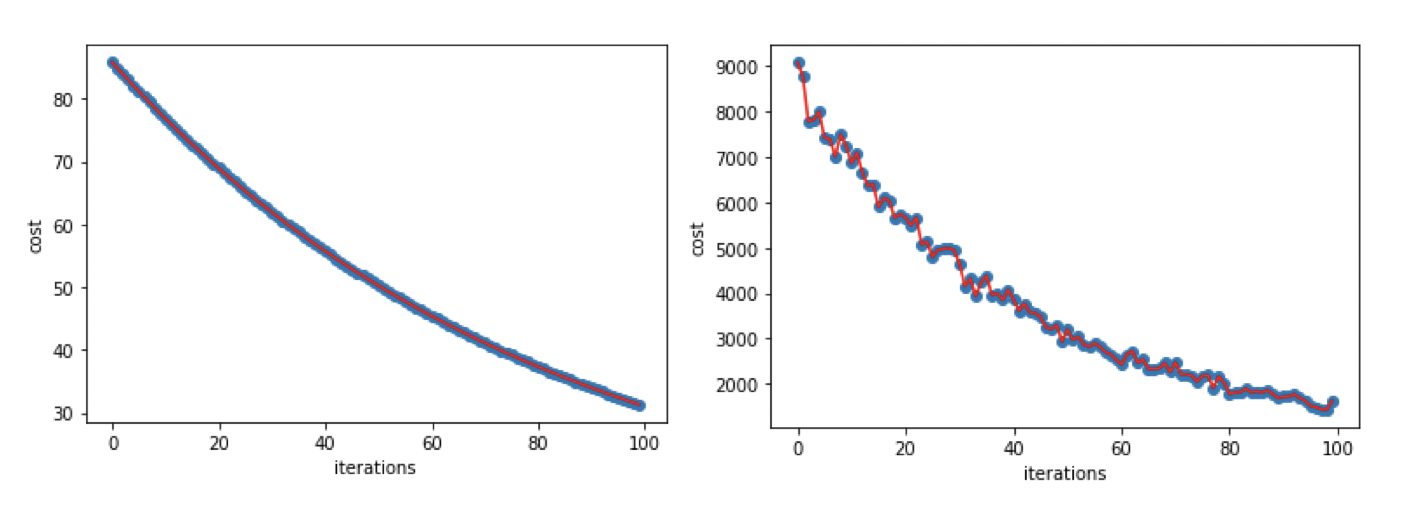(左: 最急勾配法、右: SGD)
Momentum SGD
シンプルなSGDだと、上下の振りが大きい場合、中々収束してくれないという問題が発生します。それを解決するのに、Momentum term (慣性項) を足した SGD が生み出されました。
$\theta_t$ を時点tでのパラメターとした時、$v_t$ は t-1の時のパラメターの変化、
$\gamma$ は予め設定された値で、一般的に0.9ぐらいに設定されます。
\theta_{t}=\theta_{t}-\eta \nabla J\left(\theta_{t}\right)+\gamma v_{t}
v_{t}=\gamma v_{t-1}+\eta \nabla_{\theta} J(\theta)
このmomentum項は、vt-1, vt-2, ... というように、過去の時点でのmomentumの情報を蓄積しています。これにより、アップデートを進めるにつれて、最適値への方向に押していく力が強くなっていき、収束までの時間を短くします。
Nesterov accelerated gradient
Momentum SGDの問題は、収束方向へ速く進みすぎた場合、最適値を通り過ぎてしまう可能性がある点です。
それを防ぐために、Nesterov accelerated gradient では、先に次の傾きを計算することで、最適値を通り過ぎる前に、ブレーキをかけることができます。下の２つ目の式を見ていただくとわかるよう、 $\theta-\gamma v_{t-1}$ つまりアップデート後のパラメターの推定値を使って Jの傾きを計算しています。
\theta_{t}=\theta_{t}-\eta \nabla J\left(\theta_{t}\right)+\gamma v_{t}
v_{t}=\gamma v_{t-1}+\eta \nabla_{\theta} J\left(\theta-\gamma v_{t-1}\right)
Adam
これまで見てきた勾配法では、学習率が常に一定の値でパラメターのアップデートが行われていました。
Adaptive Moment Estimation (Adam) では、学習率が最初は大きい値をとり、アップデートを進めるにつれ段々と小さくなっていく仕組みになっています。$m_{t}, v_{t}$ が Adamの Momentum項となります。mtとvtは両方とも、アップデートが進につれて指数的に小さくなっていきます。二つの違いは、 mtは平均の勾配、vtは勾配の分散を表したmomentumである点です。この２つの初期値は0ベクトルとなります。
$g=\nabla J\left(\theta_{t, i}\right)$, $\beta_{1}, \beta_{2}$ は momentum の補正値であり、γと同じ役割をします。一般的に $\beta_{1}: 0.999, \beta_{2}: 10^{-8}$ に設定されます。
$\epsilon$ は0で割るのを防ぐ為の値です。
\theta_{t+1}=\theta_{t}-\frac{\eta \cdot \hat{m}_{t}}{\sqrt{\hat{v}_{t}}+\epsilon}
\hat{m}_{t}=\frac{m_{t}}{1-\beta_{1}^{t}}
\hat{v}_{t}=\frac{v_{t}}{1-\beta_{2}^{t}}
m_{t}=\left(1-\beta_{1}\right) g_{t}+\beta_{1} m_{t-1}
v_{t}=\left(1-\beta_{2}\right) g_{t}^{2}+\beta_{2} v_{t-1}