評価関数とは?
評価関数とは、機械学習において、モデルの予測精度の評価に使われる関数です。機械学習モデルの構築では、この評価関数を最適にするパラメターが選択されます。モデルの評価関数に「損失関数」、「コスト関数」もしくは「目的関数」の三つを耳にすると思います。この三つはよく同じ意味で使われますが、それぞれ異なった定義を持っています。
まず、損失関数はある一つの点における正解の値からのずれを表した関数です。回帰問題の代表的な損失関数に、二乗誤差が挙げられます。
l(f(x_i|θ), y_i) = (f(x_i|θ)-y_i)^2
さらに分類問題では、
l(f(x_i|θ), y_i) = -t_ilog(f(x_i|θ))
など、確率分布を使った損失関数が使われます。
コスト関数はこの損失関数の全ての点の合計、もしくはそれに正則化項を加えた関数のことを示します。代表的なものに平均二乗誤差 (Mean Squared Error)が挙げられます。
MSE(θ) = \frac{1}{n} \sum (f(x_i|θ)-y_i)^2
目的関数は、さらに枠を広げて、最適化問題において、変数を変えることで、最大化もしくは最小化させ、最適なパラメーターを決定するための関数です。
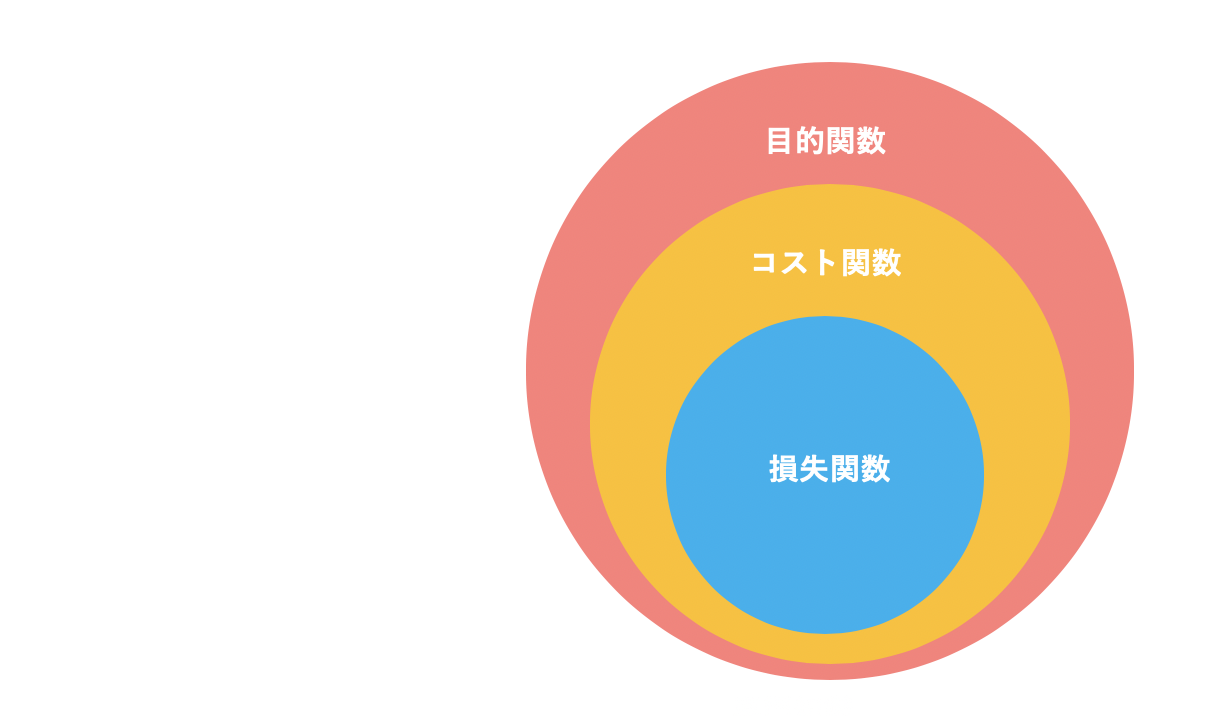 図で表すとこのような感じになります。
ただ、一般的に「損失関数」と言った時に、「コスト関数」のことを指す場合も多いのです。
図で表すとこのような感じになります。
ただ、一般的に「損失関数」と言った時に、「コスト関数」のことを指す場合も多いのです。
代表的な評価関数
回帰問題と分類問題には、それぞれ異なる損失関数が使われます。ここでは、回帰問題と分類問題それぞれで使われる代表的な評価関数を紹介します。
回帰問題の評価関数
平均二乗誤差 (Mean Squared Error)
MSE(a, b) = \frac{1}{n} \sum (y_i-(ax_i + b))^2
平均二乗誤差は回帰問題でよく使われる関数です。非常にシンプルで扱いやすいですが、外れ値に大きく影響を受けやすいのが欠点です。
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred)
二乗平均平方根誤差 (RMSE)
RMSE(a, b) = \sqrt{\frac{1}{n} \sum ((ax_i + b) - y_i) }
二乗平均平方根誤差は平均二乗誤差の平方根をとったものです。
scikit-learn では RMSE専用の実装はないので、代わりにMSEを利用します。
平均絶対誤差 (Mean Absolute Error)
MAE(a, b) = \frac{1}{n} \sum |y_i-(ax_i + b)|
平均絶対誤差は平均二乗誤差に比べて外れ値の影響を受けずらいのが特徴です。
from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_true, y_pred)
平均二乗誤差は回帰問題でよく使われる損失関数です。非常にシンプルで扱いやすいですが、外れ値に大きく影響を受けやすいのが欠点です。
Huber誤差
loss = \left\{
\begin{array}{ll}
\frac{1}{2}(f(x)-y)^2 & (|f(x) - y |\geq δ) \\
δ(|f(x) - y |)- \frac{1}{δ}& (other)
\end{array}
\right.
Huber誤差は二乗誤差(L2)と絶対値誤差(L1)の両方を取り入れた損失関数です。小さい誤差では二乗損失、大きい誤差では絶対誤差をとります。これにより、外れ値の影響を小さくできます。
分類問題の評価関数
次に分類問題における評価関数を紹介します。
機械学習において、分類問題の精度評価を議論する上で、混同行列(Confusion Matrix)の存在を忘れてはなりません。下の図は混同行列(Confusion Matrix)と呼ばれる、分類結果を種類を表した行列です。

tp = np.sum((np.array(y_true) == 1) & (np.array(y_pred) == 1))
tn = np.sum((np.array(y_true) == 0) & (np.array(y_pred) == 0))
fp = np.sum((np.array(y_true) == 0) & (np.array(y_pred) == 1))
fn = np.sum((np.array(y_true) == 1) & (np.array(y_pred) == 0))
confusion_matrix1 = np.array([[tp, fp],
[fn, tn]])
# scikit learn を使う場合:
confusion_matrix = confusion_matrix(y_true, y_pred)
Recall
Recall = \frac{TP}{TP+FN}
Recall は分類問題の精度評価関数の中でも最もシンプルなものです。真の値が正例のうち、どの程度正例として予測できているかを表しています。
from sklearn.metrics import accuracy_score
accuracy_score(y_true, y_pred)
Precision
Precisionは正例と予測したもののうち、真の正例である割合を表しています。
Precision = \frac{TP}{TP+FP}
from sklearn.metrics import precision_score
precision_score(y_true, y_pred)
F1-score
F1-score は Precision と Accuracy の調和平均をとったものです。Precision と Accuracy は互いにトレードオフの関係にあるので、F1-Score はその両方をバランスをとって考慮した評価関数です。
F1 = 2\times\frac{(Precision \times Accuracy)}{(Precision + Accuracy)}
= \frac{2TP}{2TP+FP+FN}
from sklearn.metrics import f1_score
f1_score(y_true, y_pred)
0-1 損失関数
loss = \left\{
\begin{array}{ll}
0 & (f(x)y = 1) \\
1& (f(x) y = -1)
\end{array}
\right.
0-1損失関数では、予測と正解データが一致すれば1、一致しないと0となります。
ロジスティック損失関数 (Log loss)
loss = log(1+exp(-f(x)y))
ロジスティック損失では、判別成功の場合でも、境界に近い場合は小さい損失を与えます。Cross entropy とも呼ばれています。
from sklearn.metrics import log_loss
logloss = log_loss(y_true, y_prob)
ヒンジ損失関数
loss = max(1-f(x)y,0)
ヒンジ損失は、SVMでよく使われる損失関数です。これは、ロジスティック損失と同様、境界面に近い成功にも損失を与えます。逆に判別に成功し、境界から一定以上離れた場合には損失を0にします。判別に失敗した場合は、正解から離れた分だけ、ペナルティが大きくなるような関数となっています。
ROC曲線
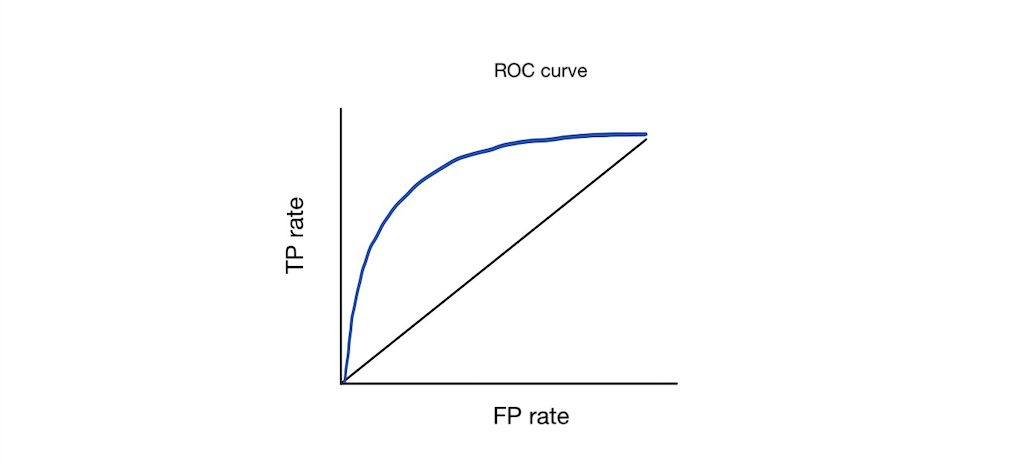
ROC曲線(Receiver Operating Characteristic Curve)は偽陽性率(FP rate)をx真陽性率(TP rate)をyととった曲線です。
この曲線の下面積を AUC (Area Under Curve)といい、予測が正しくなるほど面積が大きくなります(カーブが速く上に到達する)。完璧な予測を行った時、 (0.0, 1.0)を通り、AUCは1.0となります。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, auc
from sklearn.metrics import roc_auc_score
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
roc_auc[i] = auc(fpr[i], tpr[i])
# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])
plt.figure()
lw = 2
plt.plot(fpr[2], tpr[2], color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.show()
Gini係数
Gini係数は以下の式で表されているように、AUCと線形な関係になり、1に近いほど良いモデルとして捉えることができます。
Gini = 2 \times AUC - 1
多クラス分類の評価関数
ロジスティック損失 (Log loss)
N個のサンプルをM個のクラスに分類する時、ロジスティック損失は下の式で計算できます。
\text { multiclass logloss }=-\frac{1}{N} \sum_{i=1}^{N} \sum_{m=1}^{M} y_{i, m} \log p_{i, m}
scikitlearnは自動でマルチクラスに対応してくれます。
from sklearn.metrics import log_loss
log_loss(y_true, y_pred)
F1スコア (マルチラベル)
マルチラベル分類とは、一つのインスタンス(レコード)に対し複数の正解ラベルが存在する分類です。
例えば、ある生徒が数学、国語、理科の中から1つ以上のテストを受験した時に、それぞれ受験した科目で合格か不合格を予測するとします。
| 生徒ID | 正解 | 予測 |
|---|---|---|
| 1 | (0,1,0) | (0,1,1) |
| 2 | (0,0) | (0,0) |
| 3 | (0,1,1) | (0,1,1) |
| 4 | (0) | (1) |
この時、F1スコアは mean-F1, macro-F1, micro-F1 の3つのF1スコアの計算方法を考えます。
- mean-F1 は単純に、各レコード(生徒)のF1スコアを計算し、その平均値を全体の評価指標とします。
- macro-F1 は、クラス(科目)ごとのF1スコアを計算し、平均値を算出します。
- micro-F1 は、レコード x クラスの混同行列からF1スコアを計算します。
scikitlearn では averageを指定することで、どの計算方法を使うかを指定できます。
from sklearn.metrics import f1_score
f1_score(y_true, y_pred, average='samples')
f1_score(y_true, y_pred, average='macro')
f1_score(y_true, y_pred, average='micro')
Quadratic Weighted Kappa (順序つき多クラス問題)
Quadratic Weighted Kappa (QWK) (日本語では重み付きカッパ係数) は多クラス分類において、ラベルに順序がある時に使用する評価関数です。
例えば、レストランを4段回で評価する際、本来はランク1のお店を4と予測するのは、2と予測するより損失が大きいと考えられます。
QWKではそのような順序ありの多クラス分類に対し、以下の式で評価を行います。
\kappa=1-\frac{\sum_{i, j} w_{i, j} O_{i, j}}{\sum_{i, j} w_{i, j} E_{i, j}}
ここで
$Q_{i,j}$ は予測値の混同行列(Confusion matrix)
$E_{i,j}$ は各クラスの真の割合と観測された割合が互いに独立とした時に期待される混同行列
$w_{i,j}$ は混同行列の各マスで予測を外した時の重み ( $(i-j)^2$ として、混同行列のクラス間の距離をとることが多いです)
になります。
なんだかごちゃごちゃしていて分かり辛いですが、一言でいうと、
$E_{i,j}$ を入れることで偶然の一致を無視して、$w_{i,j}$ を入れることで、順序を考慮した評価になる
ということですね。
from sklearn.metrics import cohen_kappa_score
cohen_kappa_score(y_true, y_pred, weights='quadratic')
参照