taxi-durationコンペのデータ分析（pandas用いた基礎集計）

データ分析の練習として、pandasを用いてtaxi-duration（タクシーの利用時間を予測）のデータを分析してみました。

データセットはこちら→https://www.kaggle.com/c/nyc-taxi-trip-duration/data

データ概要

• 特徴量が10個のニューヨークタクシーの利用ログ、1458644件
• 目的変数はタクシーが乗客を乗せてから目的地点に到達するまでにかかる時間（連続値）。単位は秒

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import copy 
import matplotlib.cm as cm
%matplotlib inline

data = pd.read_csv("train.csv")
del data["dropoff_datetime"]
data['pickup_datetime'] = pd.to_datetime(data['pickup_datetime'])

data.head()

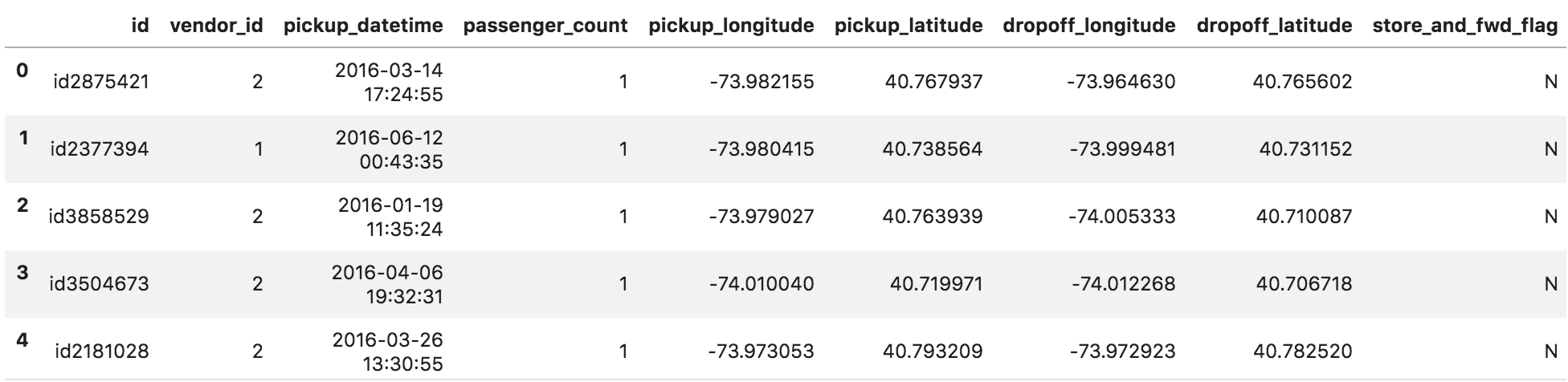
以下、順に特徴量についてEDAをして行きます。

特徴量1 idカラムについて

data["id"].nunique() == len(data)
# True

Trueが返ってくるのでダブりはありません。タクシーの利用ログだからと言ってダブりがないとは限りません。

特徴量2 vendor_idについて

data["vendor_id"].nunique()
#2

vendor_idは2種類のようです。棒グラフで比率がどんなもんか見ます。

data["vendor_id"].value_counts().plot.bar()

ラベルについて深掘りしていきたいが、kaggleのページを見ても旅行コードと紐づいているプロバイダーのidとして書かれていません。 プロバイダーを調べたいところですが、ニューヨークでタクシーを提供している会社を調べるのはだるいので、ここでは割愛します。

特徴量3 pickup_datatimeを確認する

仮説としては、日付単位で利用者数の推移をみた時に1週間単位で周期性がありそう。1日ごとの利用者数の合計としてここでは、日付でグルーピングしpassenger_countを足し合わせます。

data2 = data.copy()
data2.set_index('pickup_datetime', inplace=True)
data3 = data2.sort_index()

data_day = data3.groupby(pd.Grouper(level=0, freq='D')).sum()
data_day["passenger_count"].plot()

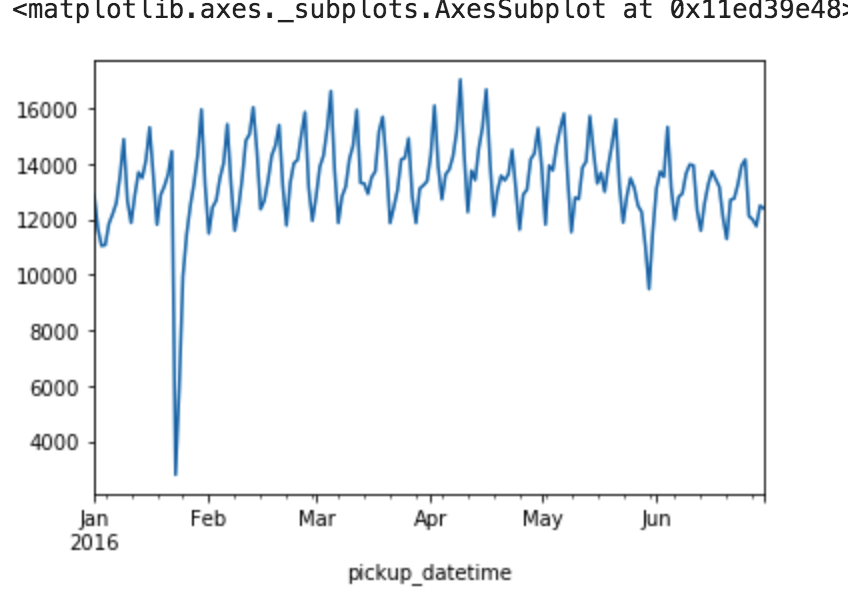
仮説通り、週間単位での周期性が見られる。一点やけに利用者数が少ない日があるので、確認する

data_week["passenger_count"].argmin()
# Timestamp('2016-01-23 00:00:00', freq='D')

1月23日に何かあったようですね。ググりまくって調べました。キング牧師の記念日の影響とか、テロの爆破予告とか色々考えましたが、個人的には以下の記事を見つけたので「記録的な暴風雪」という結論に至りました。
https://www.afpbb.com/articles/-/3074403

おそらく、休みの会社などが多く普段利用しているビジネスマンなどが利用しなかったのではないでしょうか？ついでに2016年1月23日は金曜日です。

特徴量4 passenger_countについて確認する

data["passenger_count"].value_counts().sort_values(ascending=False)

1    1033540
2     210318
5      78088
3      59896
6      48333
4      28404
0         60
7          3
8          1
9          1
Name: passenger_count, dtype: int64

乗客人数5人以上など日本では珍しい人数が無視できない割合でデータに存在する。ニューヨークタクシーでは、リムジンタクシーと呼ばれる大人数向けのタクシー送迎サービスがあるので、これらは異常値ではないと考える。乗客人数0人の60件のデータについては深掘りしていき、異常値がどうかを判断する必要がある。

data[data["passenger_count"]==0]

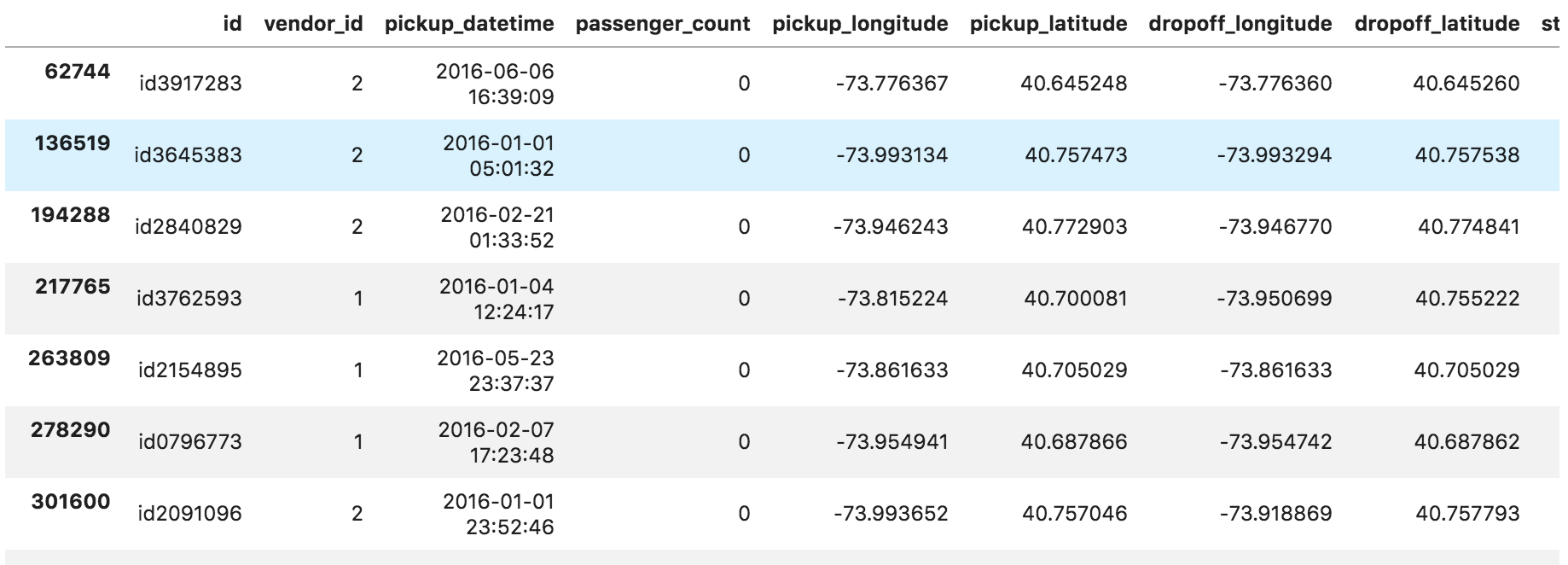
ぱっと見、乗車場所と降車場所の緯度経度が一致しているように見えるので、確認する。

len(data[data["passenger_count"]==0][(data["pickup_longitude"]==data["dropoff_longitude"])
    &(data["pickup_latitude"]==data["dropoff_latitude"])])

8

乗客人数0かつ乗車地点=降車地点のデータは8件存在する。

乗客人数0人のデータだけで要約統計量を確認する。

data_passenger_0 = data[data["passenger_count"]==0]
data_passenger_0.describe(include="all")

経度緯度から、ほとんど同じ場所だと考えられるので地理的な制約が乗客人数0人の原因と考えられる。地図検索をすると、住宅街であることが確認できる。 利用時間の中央値が20秒であることを考えると、タクシーが乗客（これから乗せる人）の場所までの移動時間のログがこれらのデータだと考えられる。 ここでの予測は、乗客を乗せた後にその乗客の目的地までかかる時間を予測することであるから、これら60件のデータは異常値として削除する。

特徴量5と６　pickup_latitudeとpickuplongtitudeについて確認する

data["pickup_latitude"].hist(bins=20)

data["pickup_longitude"].hist(bins=20)

データの分布が不均衡であることが確認できるので（データがある一部の範囲に固まっている）、実際に何%なのかを確認する。

len(data[(data["pickup_latitude"]>40.0)&(data["pickup_latitude"]<41.0)
        &(data["pickup_longitude"]> -75)&(data["pickup_longitude"]<-72)])
#1458546

len(data[(data["pickup_latitude"]>40.0)&(data["pickup_latitude"]<41.0)
        &(data["pickup_longitude"]> -75)&(data["pickup_longitude"]<-72)])/len(data)
#0.999932814312471

経度が-75°~-72°、緯度40°~41°の範囲にあるデータは1458546件あり、これは全体の99.99%以上のデータを占めている。
今回のデータがニューヨーク市内のタクシーのログデータなので、当然の結果である。この多くが存在するデータの範囲に絞ってヒストグラムを確認する。

data["pickup_latitude"].hist(bins=50,range=(40.62, 40.88))

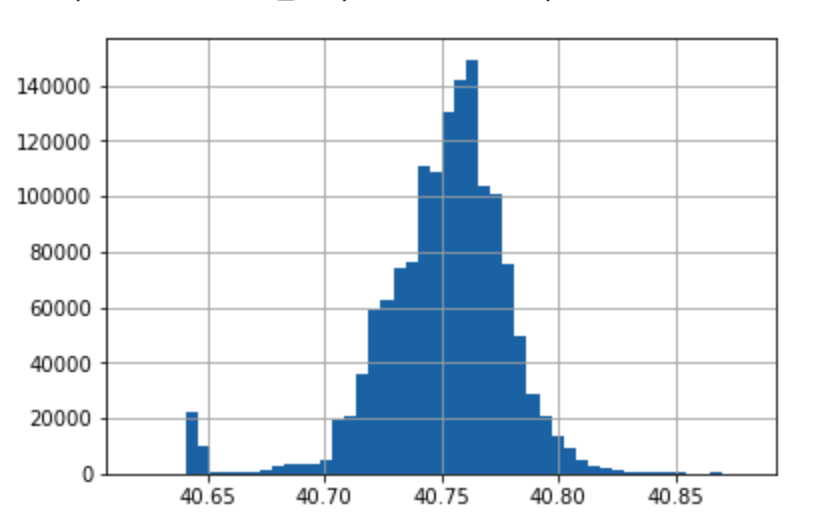
data["pickup_longitude"].hist(bins=50,range=(-74, -73.7))

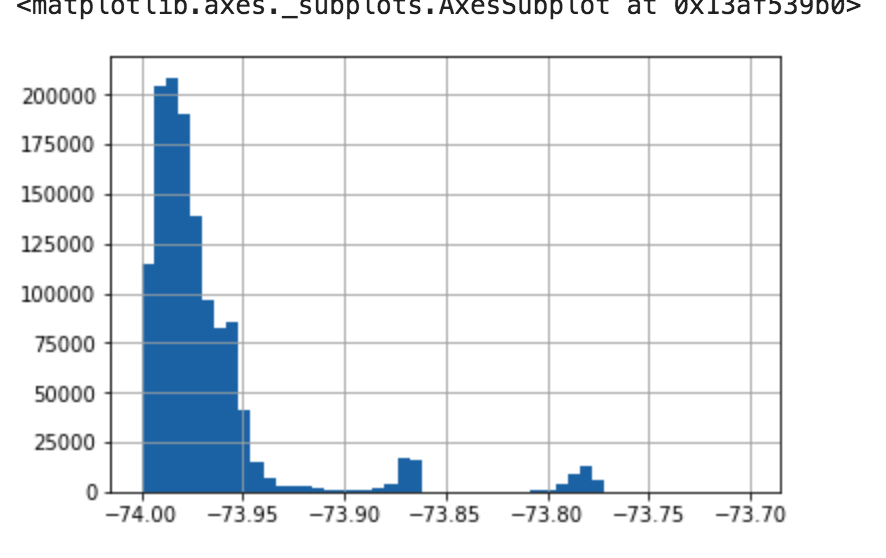
上記のヒストグラムのレンジの数値指定はいくつか試して見た目が良さそうなものを選んでいます。ビンの数も同様です。ビンの数は理論的に決める方法もありますが、今は大まかな分布がわかれば良いので、決め打ちです。

特徴量7 store_and_fwd_flagについて確認する

data["store_and_fwd_flag"].value_counts()

N    1450599
Y       8045
Name: store_and_fwd_flag, dtype: int64

割合を確認します。

###データ###
data2 = data["store_and_fwd_flag"].value_counts().values
label = ["N", "Y"]
###綺麗に書くためのおまじない###
plt.style.use('ggplot')
plt.rcParams.update({'font.size':15})
###各種パラメータ###
size=(5,4.5)
col=cm.cool(np.arange(len(data2))/float(len(data2)))
###pie###
plt.figure(figsize=size,dpi=100)
plt.subplots_adjust(left=0,right=0.7)
plt.pie(data2,colors=col,counterclock=False,startangle=90,autopct=lambda p:'{:.1f}%'.format(p) if p>=5 else '')

ラベルの不均衡性を示すのに、棒グラフ使うのか円グラフ使うのか、グラフは何も表示しないで、カウント数だけ表にして見せるのかなど、見せ方のテクニックでデータ分析のセンスが問われる気がします（自分はないです）。

ついでに簡単にそれぞれのラベルが何を意味しているのかについて論じます。

ラベルY（圧倒的に少ない方）
これは、タクシー配送ベンダーとそのタクシー車両にサーバー接続がされていないがために車両上のメモリに旅行記録が保持されているかどうかを意味します。Yなので、車両メモリに保持されている、つまり、サーバー接続がされていない方ということになります。分析要件によりますが、ベンダーに送られていない車両のデバイスに記録されている情報なんてあてになるのかな？場合によっては、yのデータは正確性という意味でかけるので、全部削除ということも考えられますね。

ラベルN（圧倒的に多い方）
上とは逆で車両メモリに保持されていないもの、つまりサーバー接続され旅行記録がベンダーに送られていたものと考えられます。

正直、この辺はkaggleのデータの説明+自分の推測なのでデータの正確な解釈ができていないです。

特徴量についてのEDAは以上です。こうやって一つ一つ丁寧に見ていくと知見が得られて面白いですね。まだ見ていない特徴量が3つありますが、pickupと対をなす特徴量なので、今は控えます。特徴量生成の際に必要になればまた見ます。

それでは今回の目的変数について確認します。

目的変数（目的地点までの時間）

今回の目的変数は連続値なので、ヒストグラムで分布を見てみます。

data["trip_duration"].hist(bins = 1000, range=(0,10000))

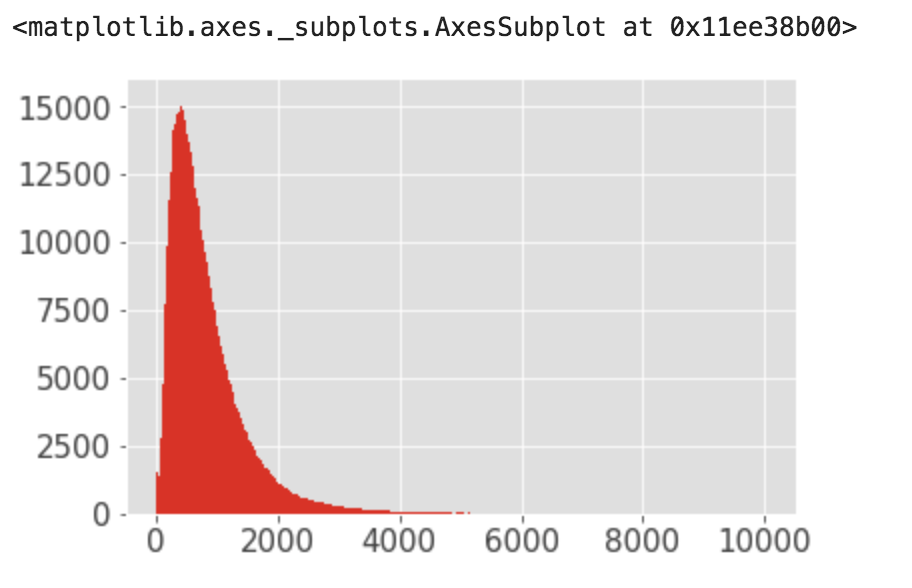
多くのデータが2000sec未満であり、一部3000000secなどの時間が見られるためこれらについて異常値がどうか判断するため詳細に見ていく

data[data["trip_duration"]>10000]

上記のレコードのうち、上から3番目のレコードの乗車地点と目的地点までの移動時間をgooglemapで調べると、予定時間15分（900sec）と計算される。実際のデータは 86352sec(約24時間)となっているので、ログ取得の際の恣意的な操作が原因と考えられる。 このデータを見てみると、多くがtrip_duration86400sec付近になっているので、ログ取得は一日ごとに自動で更新される仕組みになっていると仮説が立てられる。

ここでは、まず3時間以上の利用は異常値として分析をしていくことにする。

len(data[(data["trip_duration"]>86000)&(data["trip_duration"]<86400)])/len(data[data["trip_duration"]>10８00])

異常値と仮定した42%が86000sec(23.9時間)以上、86400sec（24時間）未満のログである。これらのデータについては仮説通り、ログ取得が恣意的な 操作によって失敗してると考えられるため、本分析においては異常値として除去する。

残りのtrip_durationが10000以上、86000未満のデータについても中身を確認する

data_eda = data[(data["trip_duration"]<86000)&(data["trip_duration"]>10000)]
data_eda[data_eda["trip_duration"]==11477]

上記データについて、googleマップで移動距離、移動時間を確認すると、タクシーで37分と表示される。渋滞などを考慮すると11477/3600=約3時間はまだ現実的な範囲である。 異常データとみなす閾値を3時間とすると交通状況などにより実際に起こりうるデータも異常と皆し兼ねない。

一般的に移動距離が長くなるほど、到達時間も長くなる。さらに利用時間が長くなればタクシーが渋滞に捕まる可能性が高くなることも考えると、移動時間と移動距離から異常値の閾値を決めるのは困難である。

まずは、移動距離が長くなると、到達時間が長くなるという仮説を検証するため、移動距離と到達時間の相関をみる。

手元のデータには経度、緯度の情報しかないので、これらのデータから実際の移動距離（ユークリッド距離）に変換する必要がある。経度、緯度からユークリッド距離に変換するコードはこちらを引用した。https://gist.github.com/rochacbruno/2883505

import math

def distance(origin, destination):
    lat1, lon1 = origin
    lat2, lon2 = destination
    radius = 6371 # km

    dlat = math.radians(lat2-lat1)
    dlon = math.radians(lon2-lon1)
    a = math.sin(dlat/2) * math.sin(dlat/2) + math.cos(math.radians(lat1)) \
        * math.cos(math.radians(lat2)) * math.sin(dlon/2) * math.sin(dlon/2)
    c = 2 * math.atan2(math.sqrt(a), math.sqrt(1-a))
    d = radius * c

    return d

start_loc = data[["pickup_longitude", "pickup_latitude"]].values.tolist()
end_loc = data[["dropoff_longitude", "dropoff_latitude"]].values.tolist()
stock = []
for start,end in zip(start_loc, end_loc):
    euclid = distance(start,end)
    stock.append(euclid)

data["distance"] = stock

data_dist = data[(data["trip_duration"]<1000000)&(data["distance"]<10)]
dist = data_dist["distance"]
duration = data_dist["trip_duration"]
x_line = [x*7200 for x in range(11)]
plt.plot(x_line, color = "b")
plt.scatter(dist,duration)

上の散布図から、仮説は間違っており、移動距離に関係なく、到達時間80000secを超えているデータが一定数存在する。他にも、移動距離（横軸）の増加に対して、異常に到達時間がかかっているデータが存在する。

今回は、距離と時間の関係から異常データを決めるのは困難であるため**「人間が一回の利用でタクシーに乗っていられる現実的な時間」**として、閾値を決めることにする。

さらに範囲を絞って分布を確認してみる。

data_dist = data[(data["trip_duration"]<5000)&(data["distance"]<10)]
dist = data_dist["distance"]
duration = data_dist["trip_duration"]
x_line = [x*7200 for x in range(11)]
plt.ylim(0,5000)
plt.plot(x_line, color = "b")
plt.scatter(dist,duration)

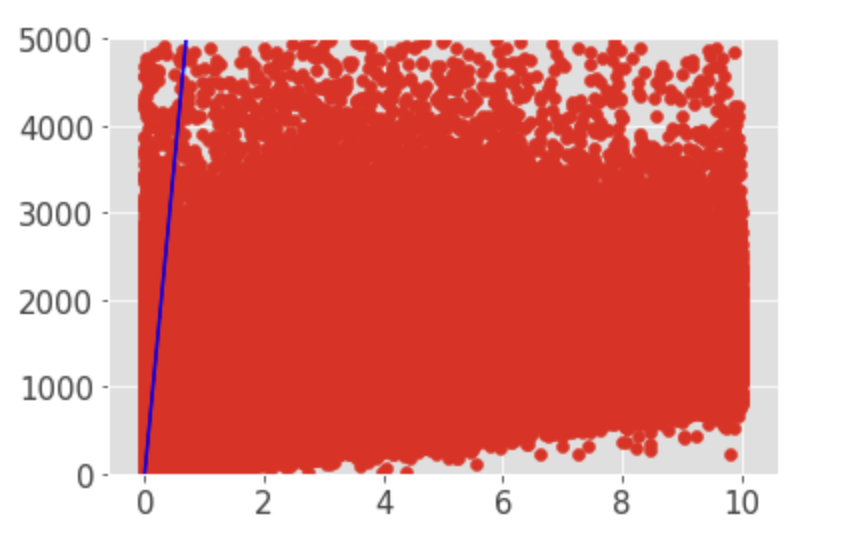
範囲を絞って確認すると、大部分のデータが移動距離と移動時間に相関がないことが確認できる（ピアソン相関係数0.1以下）。これまでの分析の結果、異常値とみなし、 予測モデルの学習に使用しないデータは以下のデータである。

• 1日の活動時間を12時間とすると、12＊3600=43200秒以上の利用は、ログ取得（※）の際の人為的ミスと考えられるので、本分析においては trip_duration>43200sec以上のデータは異常値として扱うことにする。
• 1km移動するのに2時間以上かかっているデータ.要するに上の散布図で$y=7200x$(3600sec*2)の青い直線より上のデータ点も異常値として削除する。

最後に

モデリングは別の記事で書こうと思います。モデリングしなくても一つのテーブルデータをこうやって分析するだけでも多くの知見が得られたので、満足しています。

本当はデータ分析の難しさは、複数のテーブルデータを扱うようになってからが本番だと思っています。

マーケティング系のデータではよくありますが、ユーザー情報が格納されているテーブル（基本的にユーザーでユニーク）とユーザーの使用履歴（トランザクション情報やwebサービスならログイン履歴）は別のテーブルで存在します。これらをマージする時のPK(Primary Key)チェック、innerでいくのか、leftで行くのか、抜け落ちたデータはどうするか、Nullで水増しされた分はどうするかなど、扱うファイルが複数になった途端、データ分析はコーディング、モデリング（データ作成）の両方の面で難しくなると思っています。

次自分で分析するときはその辺が体験できる、難しすぎず、ビッグデータすぎないデータに取り組もうと思います。