もともとは、日本ディープラーニング協会 E資格対策用に自学速習資料として作っていました。ただ、ディープラーニング全般を浅く、ほどよく広く学んだ人の復習用に使えそうな気もします。
*まだ作りかけです
TODO
- アテンション機構
- メモリネットワーク
- 参考文献
- 試験終わったらもうすこし範囲を広げて厚くする
※ソースは、桁あふれなどの考慮はしてません。
行列
- 特異値分解
A = U \Sigma V^{\mathrm{T}}
確率
| 分布 | 確率密度(質量)関数 | 期待値 | 分散 |
|---|---|---|---|
| 離散確率分布 | $f_X(x)=P(X=x)$ | $\sum_{i} x_i p_i $ | $\operatorname{E}[X^2]-\operatorname{E}[X]^2 $ |
| ベルヌーイ分布 | $f(x;p)=p^x(1-p)^{1-x}$ | $p$ | $p(1-p)$ |
| マルチヌーイ分布 | * | $np_i$ | $np_i (1-p_i )$ |
| ガウス分布 | $f(x)=\frac{1}{\sqrt{2\pi \sigma^2}} \exp \left( -\frac{(x-\mu)^2}{2\sigma^2} \right) $ | $\mu$ | $\sigma^2$ |
*マルチヌーイ分布の確率密度関数
f(x_1 ,\cdots ,x_k ;n,p_1 ,\cdots ,p_k )=\begin{cases}
\dfrac{n!}{x_1 !\cdots x_k !} p_1^{x_1} \cdots p_k^{x_k} &\text{when } \sum_{i=1}^k x_i =n \\[1ex]
0 &\mbox{上記以外}
\end{cases}
条件付き確率
$$
\operatorname{P}(A\mid B)=\frac{\operatorname{P}(A \cap B)}{\operatorname{P}(B)}
$$
$$
\operatorname{P}(A \cap B)= \operatorname{P}(B)\operatorname{P}(A\mid B) = \operatorname{P}(A)\operatorname{P}(B\mid A)
$$
ベイズの定理
$$
\operatorname{P}(A\mid B)=\frac{ \operatorname{P}(A)\operatorname{P}(B \mid A)}{\operatorname{P}(B)}
$$
情報
自己情報量
事象$E$が起こる確率を$\operatorname{P}(E)$とするとき、 事象$E$が起こったことを知らされたとき受け取る(選択)情報量$\operatorname{I}(E)$は
$$
\operatorname{I}(E) = −\log \operatorname{P}(E)
$$
平均情報量(エントロピー)
$ \Omega $ を、台が有限集合である確率空間とする。$ \Omega $ 上の確率分布Pが与えられたとき、各事象$ A\in \Omega $ の選択情報量$-\log \operatorname{P}(A)$の期待値は
$$
H(P) = - \sum_{A\in\Omega} P(A) \log \operatorname{P}(A)
$$
$X$ の取りうる値は 0,1 の2値。それぞれの値が生じる確率は $1−p,p$ であるから、 エントロピーは
$$
\left. H(X)= - p \log{p} - (1-p)\log{(1-p)} \right.
$$
KL情報量
\begin{align}
D_{\mathrm{KL}}(P\|Q) &= \sum_i P(i) \log \frac{P(i)}{Q(i)} \\
&= -\sum_x p(x) \log q(x) + \sum_x p(x) \log p(x)
\end{align}
機械学習
検証方法
- k-分割交差検証法
- ホールドアウト法
- 回帰問題の評価指標、相互誤差、決定係数
損失関数
二乗和誤差
L = \frac{1}{2}\sum^K_k (y_k - t_k)^2
def mean_squared_error(y, t):
loss = np.sum((t - y)**2)
return loss
バイナリクロスエントロピー
2値分類におけるクロスエントロピー
$$
L = - t \log{y} - (1-t)\log{(1-y)}
$$
def binary_cross_entropy(y, t):
loss = -1 * (t * np.log(y) + (1 – t) * np.log(1 – y))
return loss
クロスエントロピー
多クラス分類におけるクロスエントロピー
L = -\sum_k^K t_k \log y_k
def cross_entropy(y, t):
loss = -np.sum(t * np.log(y))
return loss
行列積
class MatMul(object):
def __init__(self, x1, x2):
self.x1 = x1
self.x2 = x2
def forward(self):
y = np.dot(self.x1, self.x2)
self.y = y
return y
def backward(self, grad):
grad_x1 = np.dot(grad, self.x2.T)
grad_x2 = np.dot(self.x1.T, grad)
return (grad_x1, grad_x2)
全結合層
class Affine:
def __init__(self, W, b):
self.W =W
self.b = b
self.x = None
self.original_x_shape = None
# 重み・バイアスパラメータの微分
self.dW = None
self.db = None
def forward(self, x):
# テンソル対応
self.original_x_shape = x.shape
x = x.reshape(x.shape[0], -1)
self.x = x
out = np.dot(self.x, self.W) + self.b
return out
def backward(self, dout):
dx = np.dot(dout, self.W.T)
self.dW = np.dot(self.x.T, dout)
self.db = np.sum(dout, axis=0)
dx = dx.reshape(*self.original_x_shape) # 入力データの形状に戻す(テンソル対応)
return dx
活性化関数
シグモイド
f(x) = \frac{1}{1+e^{- x}}
$x$に関する$f(x)$の微分は、
\frac{\partial f(x)}{\partial x} = f(x)(1-f(x))
class Sigmoid(object):
def __init__(self):
self.params, self.grads = [], []
self.out = None
def forward(self, x):
out = 1 / (1 + np.exp(-x))
self.out = out
return out
def backward(self, dout):
dx = dout * (1.0 - self.out) * self.out
return dx
ReLU
f(x) = \max(0, x) \\
\mbox{または、} \\
f(x) = \begin{cases}
x & (x>0) \\
0 & (x\leqq0)
\end{cases}
$x$に関する$f(x)$の微分は、
\frac{\partial f(x)}{\partial x} = \begin{cases}
1 & (x>0) \\
0 & (x\leqq0)
\end{cases}
class Relu(object):
def __init__(self):
self.mask = None
def forward(self, x):
self.mask = (x<=0)
out = x.copy()
out[self.mask] = 0
return out
def backward(self, dout):
dout[self.mask] = 0
dx = dout
return dx
LeakyReLU
f(x) = \begin{cases}
x & (x>0) \\
ax & (x\leqq0)
\end{cases}
$x$に関する$f(x)$の微分は、
\frac{\partial f(x)}{\partial x} = \begin{cases}
1 & (x>0) \\
a & (x\leqq 0)
\end{cases}
class LeakyRelu(object):
def __init__(self, a):
self.mask = None
self.a = a
def forward(self, x):
self.mask = (x<=0)
out = x.copy()
out[self.mask] = self.a*x[self.mask]
return out
def backward(self, dout):
dout[self.mask] = self.a*dout[self.mask]
dx = dout
return dx
Tanh
f(x) = \frac{\sinh x}{\cosh x} = \frac {e^x - e^{-x}} {e^x + e^{-x}}
= \frac{e^{2x} - 1} {e^{2x} + 1}
$x$に関する$f(x)$の微分は、
\frac{\partial f(x)}{\partial x} = (1-f(x)^2)
class Tanh:
def __init__(self):
self.params, self.grads = [], []
self.out = None
def forward(self, x):
y = np.tanh(x)
self.y = y
return y
def backward(self, dout):
dx = dout * (1.0 - self.out**2)
return dx
Hardtanh
f(x) = \begin{cases}
-1 & (x < -1) \\
x & (-1\leqq z \leqq 1) \\
1 & (x > 1)
\end{cases}
$x$に関する$f(x)$の微分は、
\frac{\partial f(x)}{\partial x} = \begin{cases}
1 & (-1\leqq z \leqq 1) \\
0 & 上記以外
\end{cases}
最適化
| 1次 | Momentum | 物理法則に準じる動きをする。進む方向と勾配方向が同じであれば移動量が大きくなる。 |
| Nesterov AG | Momentumの改良版。次の位置を予測し、その位置の勾配も加味する。 | |
| AdaGrad | 学習が進むにつれ、見かけの学習率が減衰していく。パラメータ毎に学習率を設定する。 | |
| RMSProp | 勾配の指数移動平均を蓄積することで、過去の勾配情報よりも直近の勾配情報をより重視する。 | |
| AdaDelta | 勾配の二乗の指数移動平均と、更新量の指数移動平均を蓄積する。 | |
| Adam | RMSPropとMomentumを組み合わせたような方法。 | |
| 2次 | ニュートン法 | ヘッセ行列を使用する。 |
| 共役勾配法 | 共役方向によって逆ヘッセ行列の計算を効率化する。 | |
| BFGS | 各ステップでのヘッセ行列の近似を改良したもの。 | |
| L-BFGS | 省メモリ化したBFGS。 |
SGD
表現1
$$
\theta_{t+1} = \theta_t - \eta \frac{\partial L}{\partial \theta_t}
$$
表現2
$$
w := w - \eta \nabla Q(w) = w - \eta \sum_{i=1}^n \nabla Q_i(w)
$$
表現3
$$
\theta \gets \theta - \frac{\epsilon}{m} \nabla_\theta \sum_i L(f(x^{(i)};\theta), y^{(i)})
$$
class SGD(object):
def __init__(self, lr):
self.lr = lr
def update(self, params, grads):
for key in params.key():
params[key] -= self.lr * grads[key]
MomentumSGD
- 前時刻の勾配影響を反映する。
v_{t+1} = \alpha v_t - \eta \frac{\partial L}{\partial \theta_t} \\
\theta_{t+1} = \theta_t + v_{t+1}
class MomentumSGD:
def __init__(self, lr, momentum):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, param in params.items():
self.v[key] = np.zeros_like(param)
for key in params.key():
self.v[key] = self.momentum * self.v[key] - self.lr * grads[key]
params[key] += self.v[key]
Nesterov Accelerated Gradient
- Momentumの改良版。
- 次時刻の位置を大雑把に見積もり、そこでの勾配の大きさを用いる。
v_{t+1} = \alpha v_t - \eta \frac{\partial L}{\partial ( \theta_t + \alpha v_t)} \\
\theta_{t+1} = \theta_{t}+v_{t+1}
class NesterovAG:
def __init__(self, lr, momentum):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, param in params.items():
self.v[key] = np.zeros_like(param)
for key in params.key():
v_pre = self.v[key].copy()
self.v[key] = v_pre * self.momentum - self.lr * grads[key]
params[key] += -self.momentum* v_pre + (self.momentum+1) * self.v[key]
AdaGrad
- パラメータ方向の勾配ごとに学習率を導入した。
- 過去の勾配成分の二乗和の平方根で学習率を割る。
- すでに大きな勾配値を取ってきた方向に対しては学習率を小さくする。
h_{t+1} = h_t + \frac{\partial L}{\partial \theta_t} \odot \frac{\partial L}{\partial }{\partial \theta_t} \\
\theta_{t+1} = \theta_t - \eta \frac{1}{\varepsilon + \sqrt{h_{t+1}}} \odot \frac{\partial L}{\partial \theta_t}
class AdaGrad:
def __init__(self, lr):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, param in params.items():
self.h[key] = np.zeros_like(param)
for key in params.key():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
RMSProp
- AdaGradでは勾配の更新量は下がり続け、一度0になると二度と有限の値に戻ることはない。
- 勾配の二乗和ではなく、指数的な移動平均を用いて学習率を変化させていく。
- 移動平均をとると、過去の情報が少しずつ薄れていき、新しい情報が反映されやすくなる。
h_{t+1} = \rho h_t + (1 - \rho) \frac{\partial L}{\partial \theta_t} \odot \frac{\partial L}{\partial \theta_t} \\
\theta_{t+1} = \theta_t - \eta \frac{1}{\sqrt{\varepsilon + h_{t+1}}} \odot \frac{\partial L}{\partial \theta_t}
class RMSprop:
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, param in params.items():
self.h[key] = np.zeros_like(param)
for key in params.key():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)
AdaDelta
- 次元量が違うものでのスケール変換に対応した。
- 勾配の二乗の指数移動平均と、更新量の指数移動平均を蓄積する。
h_{t+1} = \rho h_t + (1-\rho)\frac{\partial L}{\partial \theta_t} \odot \frac{\partial L}{\partial \theta_t} \\
\varDelta\theta_t = - \frac{\sqrt{\varepsilon + r_t}}{\sqrt{\varepsilon + h_{t+1}}} \odot \frac{\partial L}{\partial \theta_t} \\
r_{t+1} = \rho r_t + (1- \rho) \varDelta \theta_t \odot \Delta \theta_t \\
\theta_{t+1} = \theta_t + \varDelta\theta_t
class Adadelta:
def __init__(self, rho=0.95):
self.h = None
self.r = None
self.rho = rho
self.epsilon = 1e-6
def update(self, params, grads):
if self.h is None:
self.h = {}
self.r = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
self.r[key] = np.zeros_like(val)
for key in params.keys():
rms_param = np.sqrt(self.r[key] + self.epsilon)
self.h[key] = self.rho * self.h[key] + (1 - self.rho) * grads[key] * grads[key]
rms_grad = np.sqrt(self.h[key] + self.epsilon)
dp = - rms_param / rms_grad * grads[key]
params[key] += dp
self.r[key] = self.rho * self.r[key] + (1 - self.rho)*grads[key] * dp * dp
Adam
- RMSPropとMomuntumSGDを組み合わせたような方法
m_{t+1} = \rho_1 m_t + (1-\rho_1) \frac{\partial L}{\partial \theta_t} \\
v_{t+1} = \rho_2 v_t + (1-\rho_2) \frac{\partial L}{\partial \theta_t} \\
\hat{m}_{t+1} = \frac{m_{t+1}}{1-\rho_1^t} \\
\hat{v}_{t+1} = \frac{v_{t+1}}{1-\rho_2^t} \\
\\
\theta_{t+1} = \theta_t - \eta \frac{1}{\sqrt{\hat{v}_{t+1}} + \varepsilon} \odot \hat{m}_{t+1}
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, param in params.items():
self.m[key] = np.zeros_like(param)
self.v[key] = np.zeros_like(param)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.key():
self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
CNN
畳み込み後のサイズ
$$
\mathrm{O}_h = \frac{H+2P-F}{S}+1
$$
im2col
def im2col(input_data, filter_h, filter_w, stride=1, pad=0, constant_values=0):
"""
input_data : (データ数, チャンネル, 高さ, 幅)の4次元配列からなる入力データ
filter_h : フィルターの高さ
filter_w : フィルターの幅
stride : ストライド
pad : パディング
return : 2次元配列
"""
N, C, H, W = input_data.shape
# 出力データ(畳み込みまたはプーリングの演算後)の形状を計算する
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
# パディング処理
img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)],
'constant', constant_values=constant_values)
col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))
# 配列を並び替える(フィルター内のある1要素に対応する画像中の画素を取り出してcolに代入する)
for y in range(filter_h):
#フィルターの高さ方向のループ
y_max = y + stride*out_h
for x in range(filter_w):
#フィルターの幅方向のループ
x_max = x + stride*out_w
col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]
col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1)
return col
def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0, is_backward=False):
"""
col : 2次元配列
input_shape : (データ数, チャンネル, 高さ, 幅)の4次元配列からなる入力データ
filter_h : フィルターの高さ
filter_w : フィルターの幅
stride : ストライド
pad : パディング
return : (データ数, チャンネル数, 高さ, 幅)の4次元配列,画像データの形式を想定
"""
N, C, H, W = input_shape
# 出力(畳み込みまたはプーリングの演算後)の形状を計算する
out_h = (H + 2*pad - filter_h)//stride + 1
out_w = (W + 2*pad - filter_w)//stride + 1
col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)
img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1))
for y in range(filter_h):
#フィルターの高さ方向のループ
y_max = y + stride*out_h
for x in range(filter_w):
#フィルターの幅方向のループ
x_max = x + stride*out_w
if is_backward:
img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]
else:
img[:, :, y:y_max:stride, x:x_max:stride] = col[:, :, y, x, :, :]
return img[:, :, pad:H + pad, pad:W + pad]
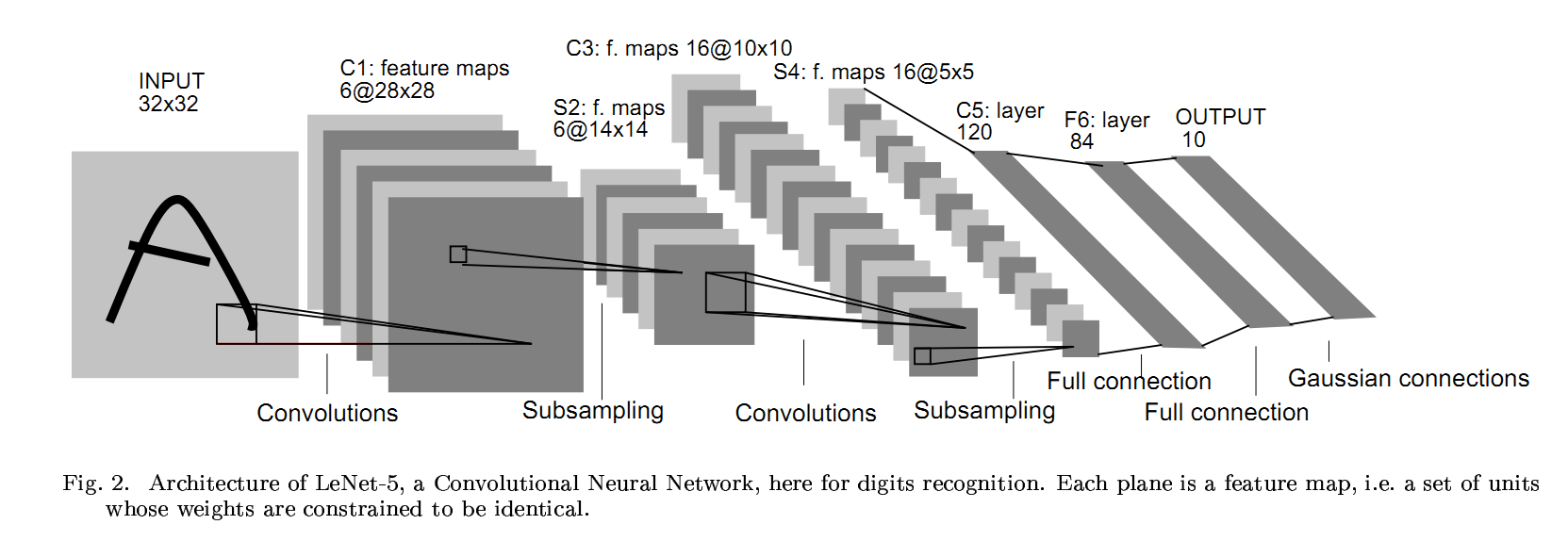
LeNet
- LeNet-5は、6層構造(CNN層が5つ)のネットワーク。
- 32x32pxのパッチ画像を入力とする。
- 1998年頃にYann LeCunらによって提案された。
- 畳み込み層の考え方は、1989年頃から提案された。
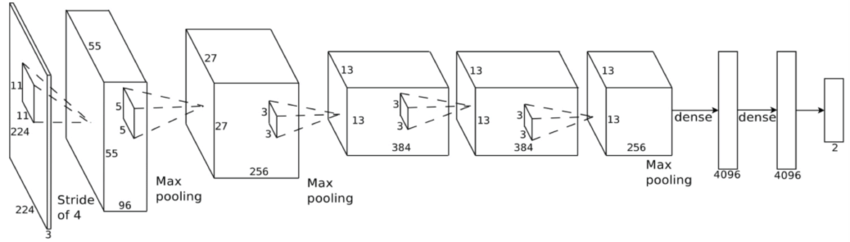
AlexNet
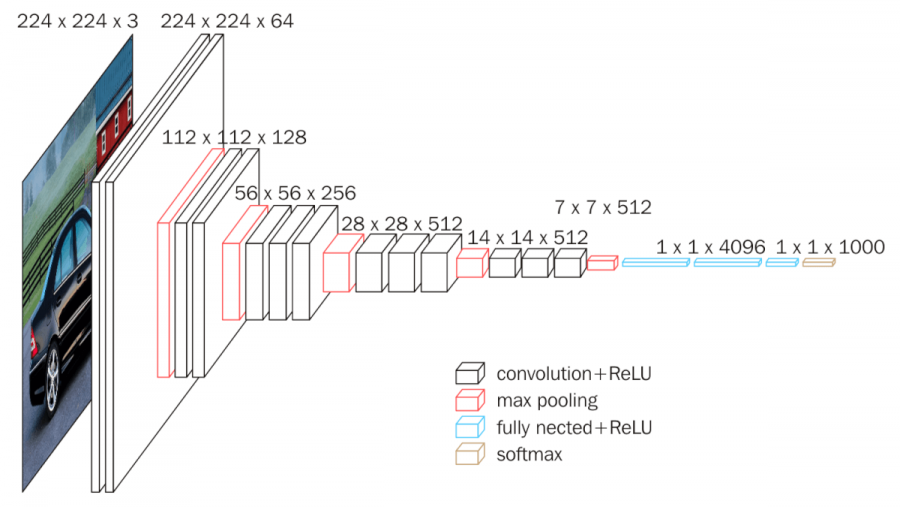
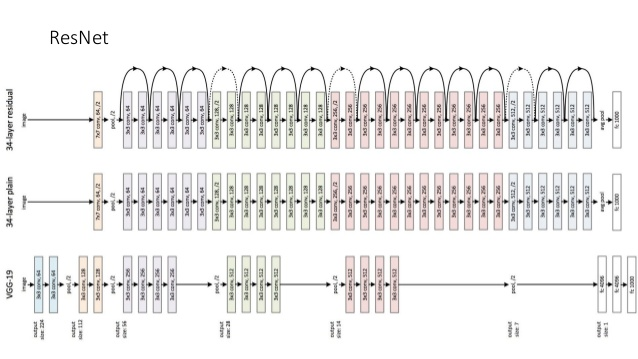
VGG
- 2014年のILSVRCで2位になったネットワーク。
- AlexNetよりも深いネットワーク構造(16/19)。
- パラメータ数は約1億4,000万個
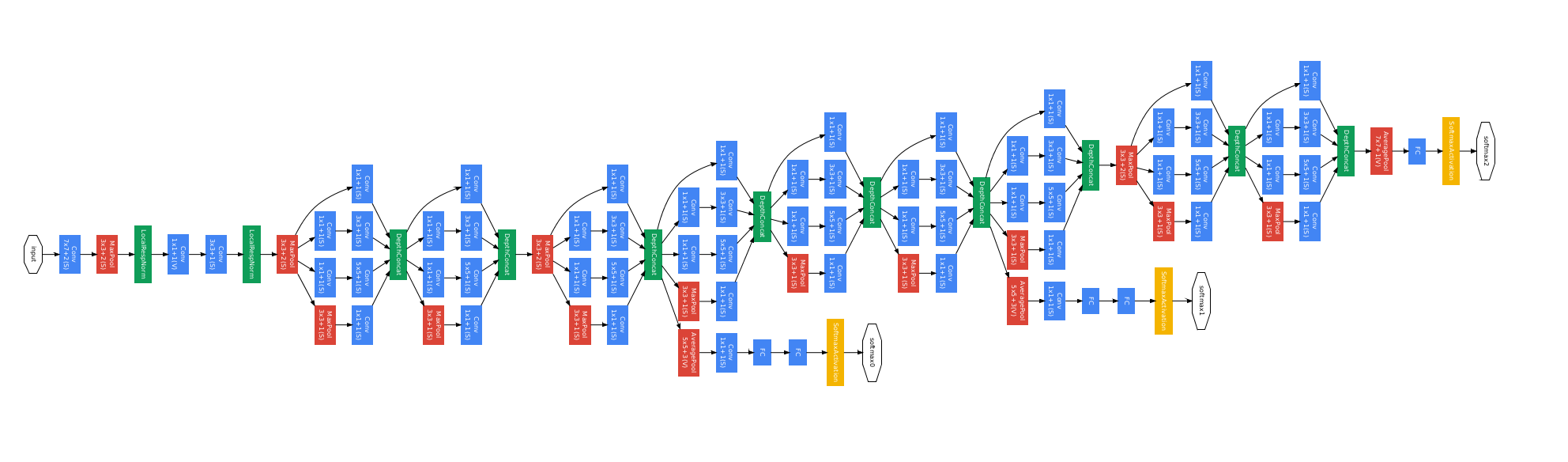
GoogLeNet
- 2014年のILSVRCで1位になったネットワーク。
- Inception module
- 大きな畳込みフィルタを小さな畳込みフィルタのグループで近似することで、モデルの表現力とパラメータ数のトレードオフを改善していると言える。
- 1*1の畳み込みフィルタが使われているが、このフィルターは次元削減と等価な効果がある。
- 小さなネットワークを1つのモジュールとして定義し、モジュールの積み重ねでネットワークを構築する。
- Auxiliary Loss
- ネットワークの途中から分岐させたサブネットワークにおいてもクラス分類を行う。
- AuxililaryLossを導入しない場合でもBatch Normalizationを加えることにより、同様に学習がうまく進むことがある。
- アンサンブル学習と同様の効果が得られるため、汎化性能の向上が期待できる。
ResNet
- 2015年のILSVRCで1位になったネットワーク。
- Residual Block
- ブロックへの入力似これ以上の変換が必要ない場合は重みが0となり、小さな変換が求められる場合は対応する小さな変動をより見つけやすくなることが期待される。
- Identity mapping
- 層をまたがる結合のこと。このショートカット結合により、逆伝播時に購買が減衰していくことを抑えることができる。
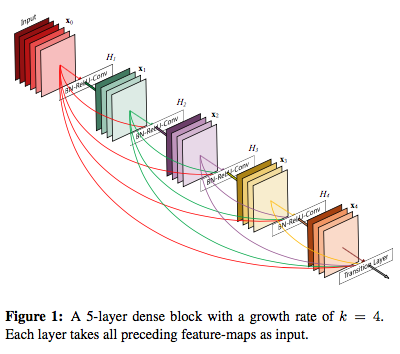
DenseNet
- ResNetに似たショートカット結合を持つネットワーク。
- 特徴量を再利用する結合になっている。
- DenseBlockによって構成される。
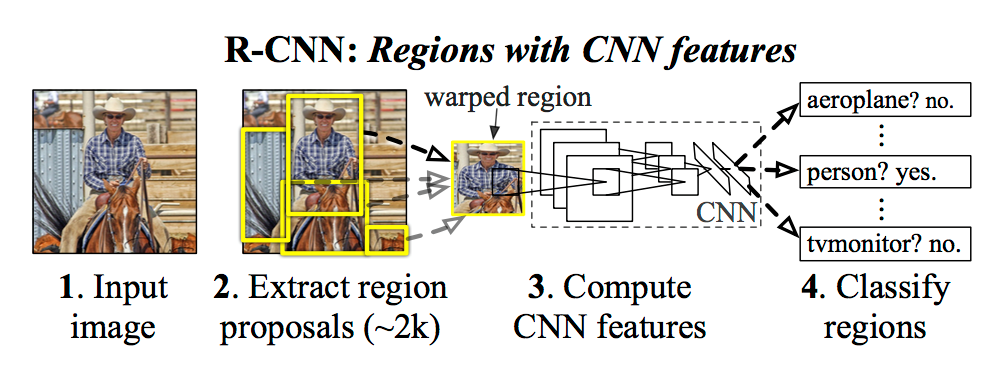
R-CNN
- 物体候補領域画像をアスペクト比を保たずリサイズして、CNNで特徴を取り出す。
- 特徴抽出のCNN、カテゴリ推定のSVMなど各学習の目的ごとに別々に学習させる必要がある。
手順
- 入力画像に対して、物体が写っている領域の候補を選択的検索法(Selective Search) で約2,000個抽出する
- CNN のインプットの大きさに合うようにそれぞれの領域中の画像をリサイズする
- それぞれの物体領域候補に対して、CNN (原著論文ではAlexNet) で特徴マップを計算する
- それぞれの領域に何が写っているかSVMで分類する
- 物体の詳細位置を決めるために、特徴マップとバウンディ ングボックス座標を回帰させる問題を解く
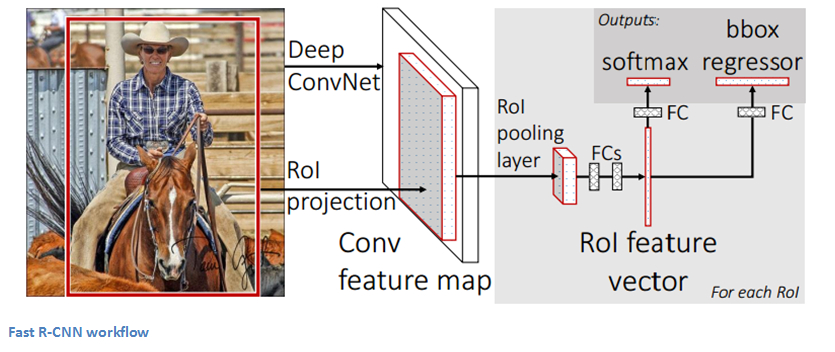
Fast R-CNN
- 画像全体を入力して計算した特徴マップをすべ ての物体領域候補で再利用することで、R-CNNを高速化させたもの。
手順
- 選択的検索法を利用して物体領域候補を算出する
- 画像全体をCNNに入力して特徴マップを計算する
- 物体領域候補ごとに以下の計算を行う
- 物体領域候補に対応する特徴マップを抽出する
- 特徴マップをRoI(Region of Interest)プーリング層に渡し、次元数の異なる特徴マップを一定の大きさのベクトルに変換する
- 物体の詳細位置を決めるために、特徴マップとバウンディングボックス座標を回帰させる問題を解く
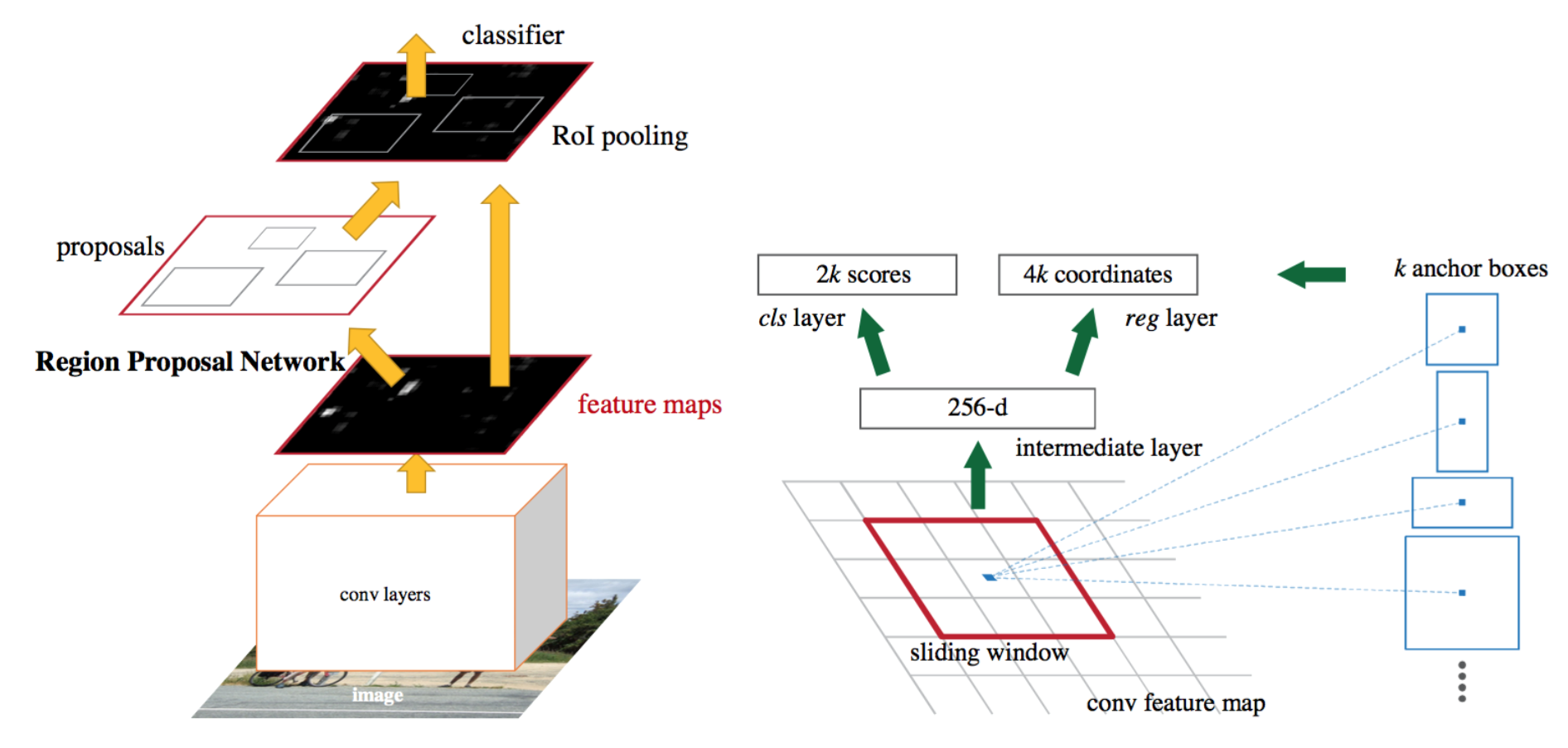
Faster R-CNN
- end-to-end学習が可能なネットワークアーキテクチャである。
- 特徴マップから物体領域候補を推定する領域提案ネットワーク(RPN)とFast R-CNNの2つのネットワークで構成される。
- 2つのネットワークで特徴マップを共有しているため、計算が効率的。
- 矩形領域回帰の誤差関数はFast R-CNNと同じ。
- CNN(conv layer)で特徴マップを生成し、RPNで領域候補を推定した後、RoI Poolingという手法で固定サイズに変形する。
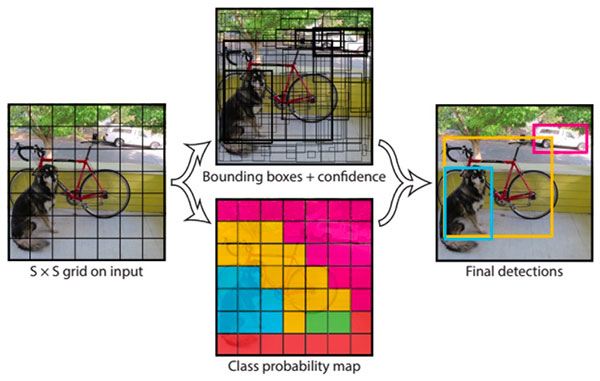
YOLO
- 画像全体をグリッドに分割(セル)し、セル毎にクラスとバウンディングボックスを求める方法。
- 検出速度は高速だが、画像内のオブジェクト同士が複数重なっている場合に上手く検出できないという欠点がある。
- セル内で出力できるクラスは1つのみ。
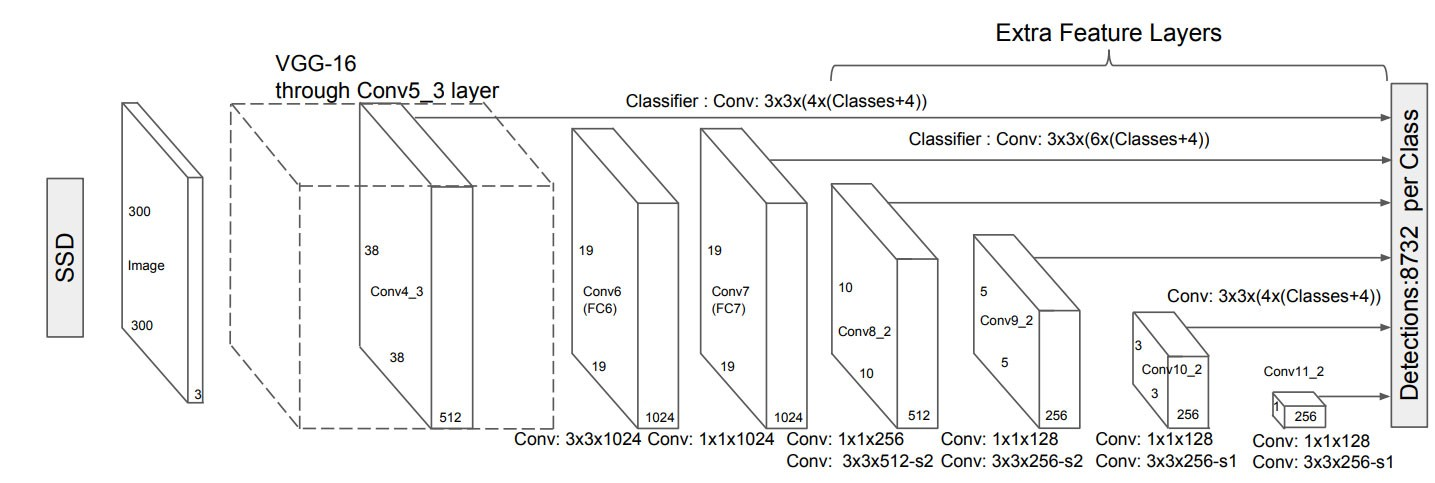
SSD
- YOLOと似たアルゴリズム。
- 様々な階層の出力層からマルチスケールな 検出枠を出力できるように工夫されている。
- NNでは、出力層に近いほど特徴マップのサイズが小さくなるので、それぞれの層の特徴マップには様々なサイズの物体を検出できる情報があるはずである。つまり、出力層に近い特徴マップほど大きな物体を検知しやすくなり、入力層に近い特徴マップほど小さな物体を検知しやすくなると考えられる。
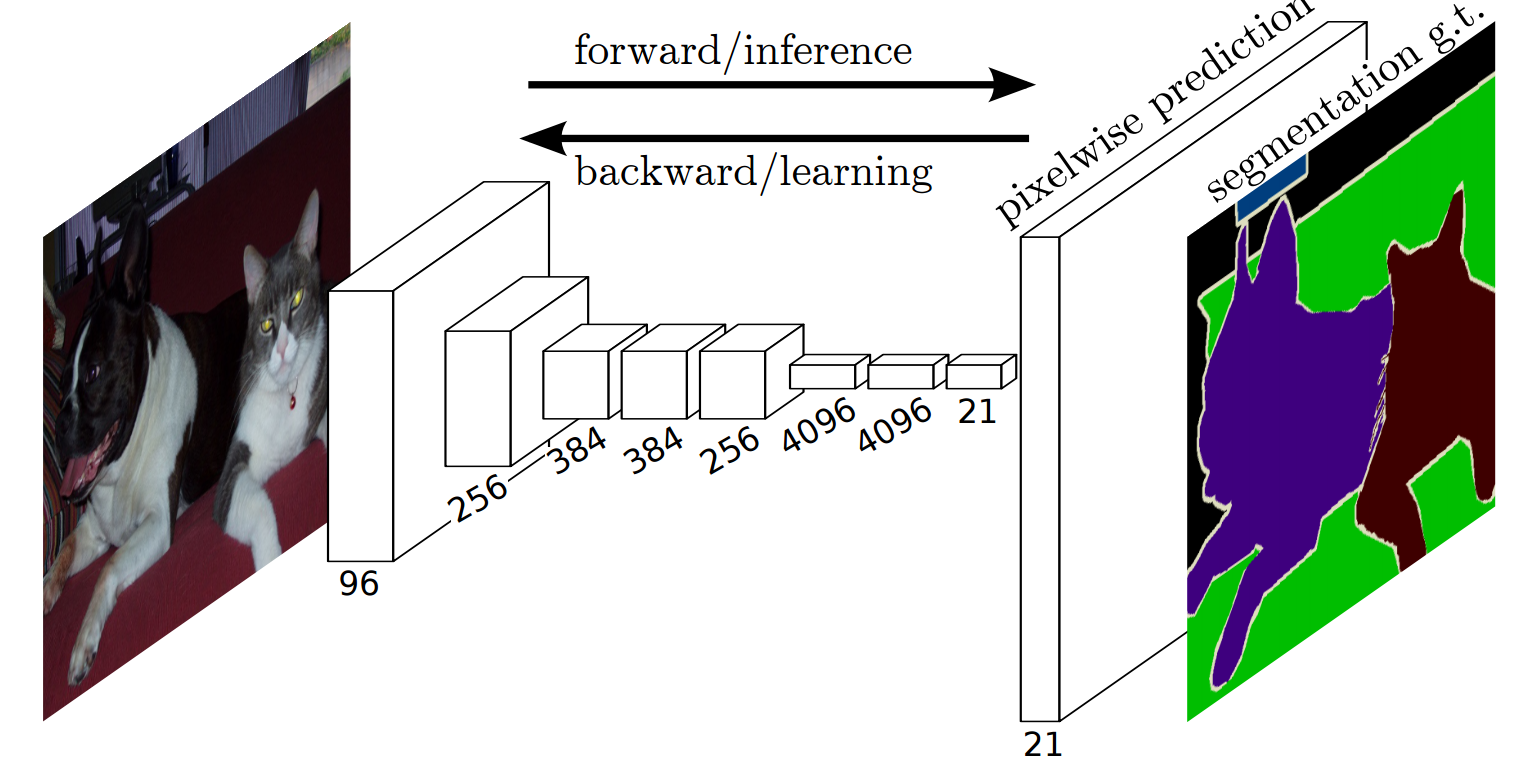
FCN
- プーリング層では、特徴マップはダウンサンプリングされる。
- プーリング層の後、逆畳込みを用いてアップサンプリングを施すことで、出力される画像サイズを大きくする。
- 損失は、ピクセルごとのクロスエントロピー誤差の合計。
- ダウンサンプリングされた特徴マップに対して単純に逆畳み込みを適用するだけでは、出力結果が粗くなってしまうため、スキップ接続を用いて情報ロスが発生する前の情報をアップサンプリング処理に入力する。
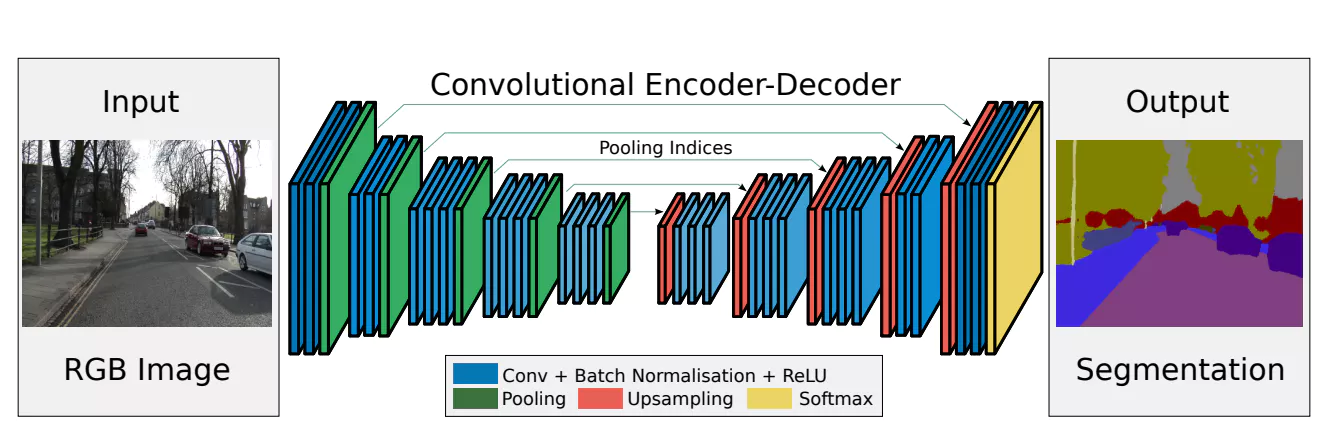
SegNet
- エンコーダ(encoder)部分とデコーダ(decoder)部分で構成されるセマンティックセグメンテーションのためのネットワーク。
- FCNのようにプーリング前の特徴をアップサンプリング層にコピーするのではなく、 エンコーダ部分のマックスプーリング層で採用した値の場所を記録しておき、デコーダ部分のアップサンプリング時にその場所を使って特徴マップを拡大する。
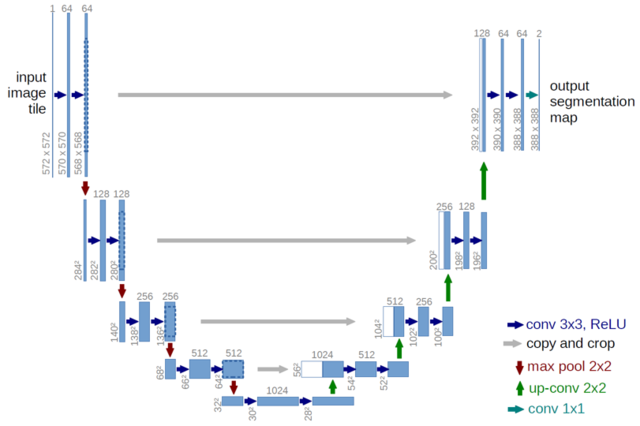
U-Net
- 横向きのパスは畳み込み
- 下向きのパスはmax-pooling
- 上向きのパスはup-conv (逆畳み込み)
- 最終的な特徴マップを1x1 convで セグメンテーションマップに変換
- FCNでは入力側の中間表現を出力側に反映する際、チャンネルごとの足し算を行っていたが、U-Netでは足し算ではなく”連結”することで入力を位置情報を保持している。
GAN
\min_G \max_D V(G,D) = \mathbb{E}_{x \sim p_{data}(x)} [\log D(x)] + \mathbb{E}_{z \sim p_{z}(z)} [\log (1 - D(G(z)))]
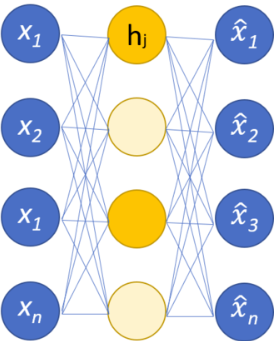
オートエンコーダ
- 特徴抽出器(次元圧縮)、ノイズ除去、階層型NNの初期パラメータの取得、復元誤差を利用した異常検知などに利用される。
- 入力層(エンコーダ)と復元層(デコーダ)に同じデータを入れて学習を行う。
- スパース自己符号化器は、自己符号化器に正則化項を加えて学習させる方法。
- 雑音除去自己符号化器は、ランダムなノイズを加えたデータを入力層に入れる方法。復元層から出てくるデータがノイズを加える前のデータに近くなるように学習させる。
- 変分自己符号化器(VAE)は、データが生成するメカニズムを仮定する(生成モデル)。
VAE
-
自己符号化器と同じように、入力を再現する学習を行う。
-
データが生成するメカニズムを仮定する点が自己符号化器と異なる。
-
潜在変数に確率分布(ガウス分布など)を仮定する。
-
Reparameterization trick
- サンプリングで誤差逆伝播法を使えないことを解決するための方法
VAEを最尤推定問題として定式化すると以下になる。
\begin{align}
\mathcal{L}(q) &= \mbox{再構成による対数尤度の期待値} - \mbox{正則化項} \\
&= \mathbb{E}_{z\sim q(z|x)}\log p_{model}(x|z) - D_{KL}(q(z|x)||p_{model}(z)) \\
\end{align}
\\
\mathbb{E}_{z\sim q(z|x)}\log p_{model}(x|z) = \sum^D_{i=1} x_i \log y_i + (1-x_i)\cdot \log(1-y_i) \\
D_{KL}(q(z|x)||p_{model}(z)) = D_{KL}(N(\mu, \Sigma)||N(O,I)) = - \frac{1}{2} \sum^J_j(1+\log(\sigma_j^2)-\mu_j^2-\sigma_j^2)
よって、損失関数は以下になる。
L=-\sum^D_{i=1}x_i \log y_i + (1-x_i) \cdot \log(1-y_i) - \frac{1}{2}\sum_j^J(1+\log(\sigma_j^2)-\mu_j^2-\sigma_j^2)
RNN
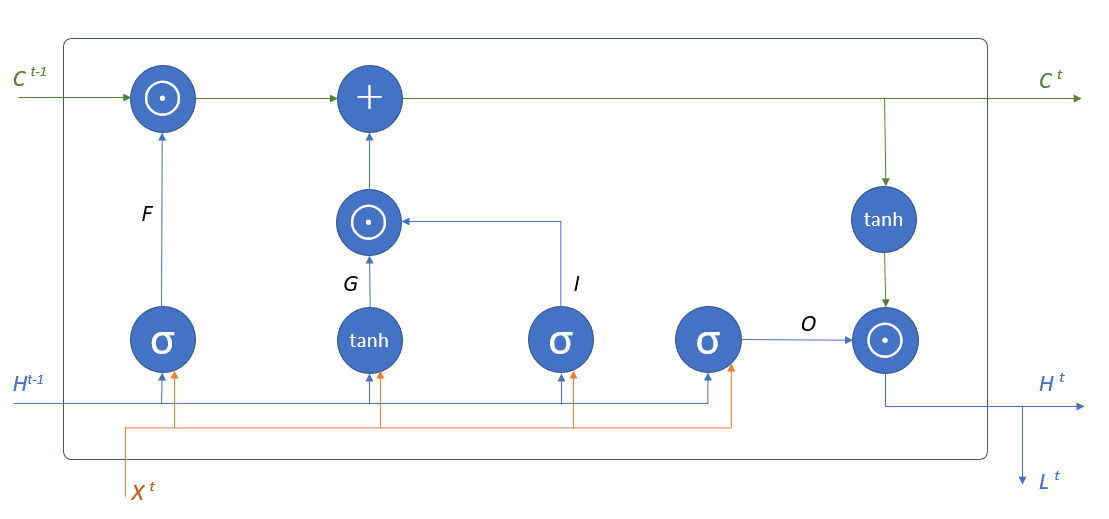
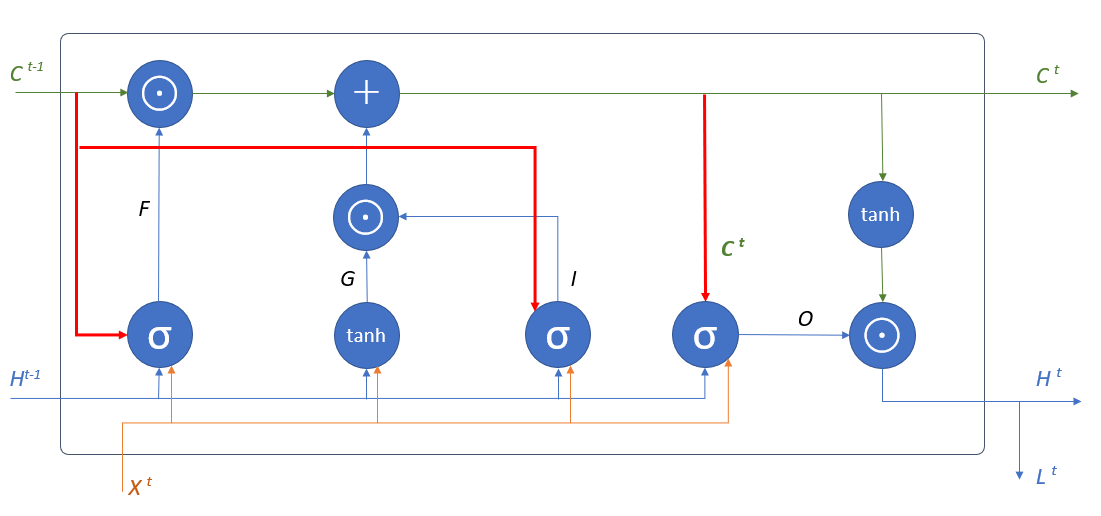
LSTM
- 出力ゲート(Output gate)
- 取り出した記憶について、各要素を弱める度合いを決めるゲート
- 忘却ゲート(Forget gate)
- 記憶セルの各要素を弱める(忘れる)度合いを決めるゲート
- 入力ゲート(Input gate)
- 記憶セルに追加されるGの各要素を弱める割合を決めるゲート
- 記憶セル(Memory cell)
- 過去の情報を記録する部分
\begin{align}
&F = \sigma \left( X^tW_x^{(f)} + H^{t-1}W_h^{(f)}+B^{(f)}\right) \\
&G = \operatorname{tanh} \left( X^tW_x^{(g)} + H^{t-1}W_h^{(g)}+B^{(g)}\right) \\
&I = \sigma \left( X^tW_x^{(i)} + H^{t-1}W_h^{(i)}+B^{(i)}\right) \\
&O = \sigma \left( X^tW_x^{(o)} + H^{t-1}W_h^{(o)}+B^{(o)}\right) \\
&H^t = O \odot \operatorname{tanh} C^t \\
&C^t = G \odot I + F \odot C^{t-1} \\
&\text{$\sigma$はシグモイド関数}
\end{align}
class LSTM:
def __init__(self, Wx, Wh, b):
'''
Parameters
----------
Wx: 入力`x`用の重みパラーメタ(4つ分の重みをまとめる)
Wh: 隠れ状態`h`用の重みパラメータ(4つ分の重みをまとめる)
b: バイアス(4つ分のバイアスをまとめる)
'''
self.params = [Wx, Wh, b]
self.grads = [np.zeros_like(Wx), np.zeros_like(Wh), np.zeros_like(b)]
self.cache = None
def forward(self, x, h_prev, c_prev):
Wx, Wh, b = self.params
N, H = h_prev.shape
A = np.dot(x, Wx) + np.dot(h_prev, Wh) + b
f = A[:, :H]
g = A[:, H:2*H]
i = A[:, 2*H:3*H]
o = A[:, 3*H:]
f = sigmoid(f)
g = np.tanh(g)
i = sigmoid(i)
o = sigmoid(o)
c_next = f * c_prev + g * i
h_next = o * np.tanh(c_next)
self.cache = (x, h_prev, c_prev, i, f, g, o, c_next)
return h_next, c_next
def backward(self, dh_next, dc_next):
Wx, Wh, b = self.params
x, h_prev, c_prev, i, f, g, o, c_next = self.cache
tanh_c_next = np.tanh(c_next)
ds = dc_next + (dh_next * o) * (1 - tanh_c_next ** 2)
dc_prev = ds * f
di = ds * g
df = ds * c_prev
do = dh_next * tanh_c_next
dg = ds * i
di *= i * (1 - i)
df *= f * (1 - f)
do *= o * (1 - o)
dg *= (1 - g ** 2)
dA = np.hstack((df, dg, di, do))
dWh = np.dot(h_prev.T, dA)
dWx = np.dot(x.T, dA)
db = dA.sum(axis=0)
self.grads[0][...] = dWx
self.grads[1][...] = dWh
self.grads[2][...] = db
dx = np.dot(dA, Wx.T)
dh_prev = np.dot(dA, Wh.T)
return dx, dh_prev, dc_prev
覗き穴結合
記憶セルの状態を各ゲートに伝えることでゲートの開き具合を決める際に記憶セルの情報を利用する。
\begin{align}
&F = \sigma \left( X^tW_x^{(f)} + H^{t-1}W_h^{(f)}+C^{t-1}W_c^{(f)}+B^{(f)}\right) \\
&G = \operatorname{tanh} \left( X^tW_x^{(g)} + H^{t-1}W_h^{(g)}+B^{(g)}\right) \\
&I = \sigma \left( X^tW_x^{(i)} + H^{t-1}W_h^{(i)}+C^{t-1}W_c^{(i)}+B^{(i)}\right) \\
&O = \sigma \left( X^tW_x^{(o)} + H^{t-1}W_h^{(o)}+C^{t}W_c^{(o)}+B^{(o)}\right) \\
&H^t = O \odot \operatorname{tanh} C^t \\
&C^t = G \odot I + F \odot C^{t-1} \\
&\text{$\sigma$はシグモイド関数}
\end{align}
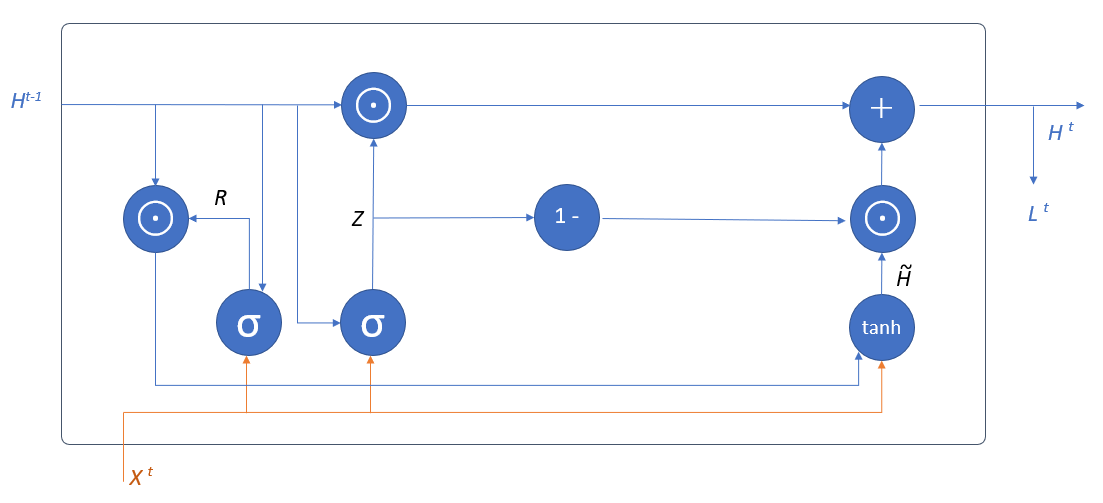
GRU
- LSTMよりパラメータの少ないゲート付きRNN
- リセットゲート
- 過去の隠れ状態をどのくらい弱めるかを決めるゲート
- 更新ゲート
- 過去と仮の隠れ状態の混合割合を決めるゲート
\begin{align}
&R = \sigma \left( X^tW_x^{(r)} + H^{t-1}W_h^{(r)}+B^{(r)}\right) \\
&Z = \sigma \left( X^tW_x^{(z)} + H^{t-1}W_h^{(z)}+B^{(z)}\right) \\
&\widetilde{H} = \operatorname{tanh} \left( X^tW_x^{(\widetilde{h})} + (R \odot H^{t-1})W_h^{(\widetilde{h})}+B^{(\widetilde{h})}\right) \\
&H^t = Z \odot H^{t-1} + (1-Z) \cdot \widetilde{H}
\end{align}
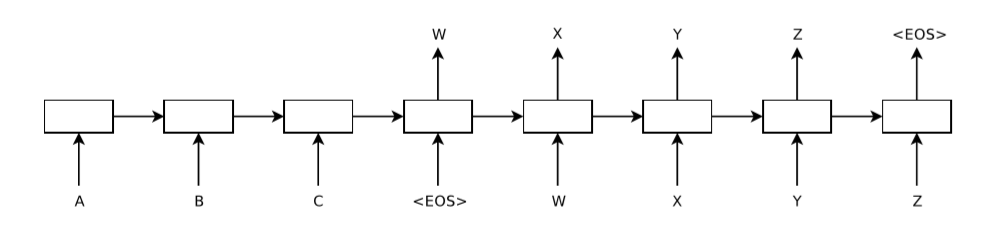
seq2seq
- sequence-to-sequence
- RNN版エンコーダー・デコーダ
- 入力系列の長さと出力系列の長さは一致しなくても良い。
- 系列の長さは、データによって異なっていても良い。
アテンション機構
- 系列が長くなると、最初に入力された情報がデコーダ側まで伝播しづらくなるため、LSTMのようなゲート付きRNNを使っても学習が難しい。
- このような課題をアテンションによって対処。
- ソフトアテンション
- 確率分布による重み付き平均をとる
- seq2seqモデルで用いるアテンション
- ハードアテンション
- 確率分布に従って1点だけに注目する方法
- アテンションを行うためのレイヤはエンコーダとデコーダの間に位置づけられる。
- アテンション付き系列変換モデルは、全時刻の中間状態を参照する。
- その際に重要な中間状態をより重視するように参照する。
メモリネットワーク
強化学習
- 動的計画法 ・・・環境のモデルが既知の場合にベルマン方程式を解いて最適な方策を得る
- 方策反復法
- 価値反復法
- モンテカルロ法 ・・・ 実際に思考を繰り返して得られた報酬から価値を推定する
- TD学習 ・・・ 実際の報酬から方策関数や価値関数を改善しながらベルマン方程式を解く
- Sarsa
- Q学習
- DQN
- 方策勾配法
- マルチステップ学習法
- Actor-Critic
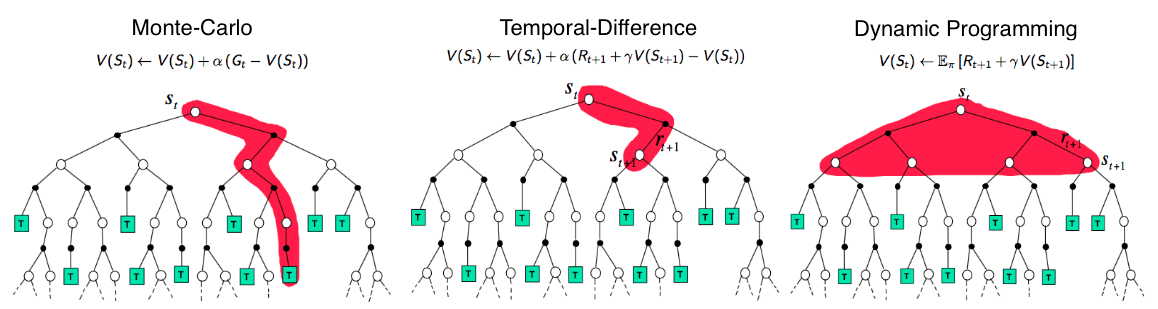
A (Long) Peek into Reinforcement Learning
ベルマン方程式
価値観数を再帰的に定義し期待値を展開したものをベルマン方程式という。ベルマン方程式が成り立つためには、マルコフ決定過程である必要がある。
状態価値に関するベルマン方程式
\begin{align}
V^\pi(s) &= \mathbb{E}^\pi[G_t|s_t=s] \\
&= \mathbb{E}^\pi \left[\gamma \sum^{\infty}_{k=0} \gamma^kr_{t+1+k}|S_t=S\right] \\
&= \mathbb{E}^\pi \left[ r_{t+1} + \gamma \sum^{\infty}_{k=0} \gamma^kr_{t+2+k}|S_t=S\right] \\
&= \sum_a\pi(a|s)\sum_{s'}P(s'|s,a)[r(s,a,s')+\gamma V^{\pi}(s')]
\end{align}
\boxed{
\begin{align}
\pi(s,a) & \mbox{:方策関数} \\
P(s'|s,a) & \mbox{:状態遷移関数} \\
r(s,a,s') & \mbox{:報酬関数}
\end{align}
}
行動価値関数に関するベルマン方程式
\begin{align}
Q^{\pi}(s,a) &= \mathbb{E}^\pi[G_t|s_t=s, a_t=a] \\
&= \mathbb{E}^\pi \left[ \sum^\infty_k \gamma^k r_{t+1+k}| s_t=s,a_t=a \right] \\
&= \mathbb{E}^\pi \left[ r_{t+1} + \sum^\infty_k \gamma^k r_{t+2+k}|s_t=s, a_t=a \right] \\
&= \sum_{s'} P(s'|s,a)[r(s,a,s')+\gamma V^\pi (s')]
\end{align}
\\
V^\pi (s) = \sum_a \pi(a|s)Q^\pi(s,a) \mbox{より、}\\
Q^\pi(s,a)=\sum_{s'}P(s'|s,a)[r(s,a,s')+\gamma \sum_a \pi(a'|s')Q^\pi(s',a')]
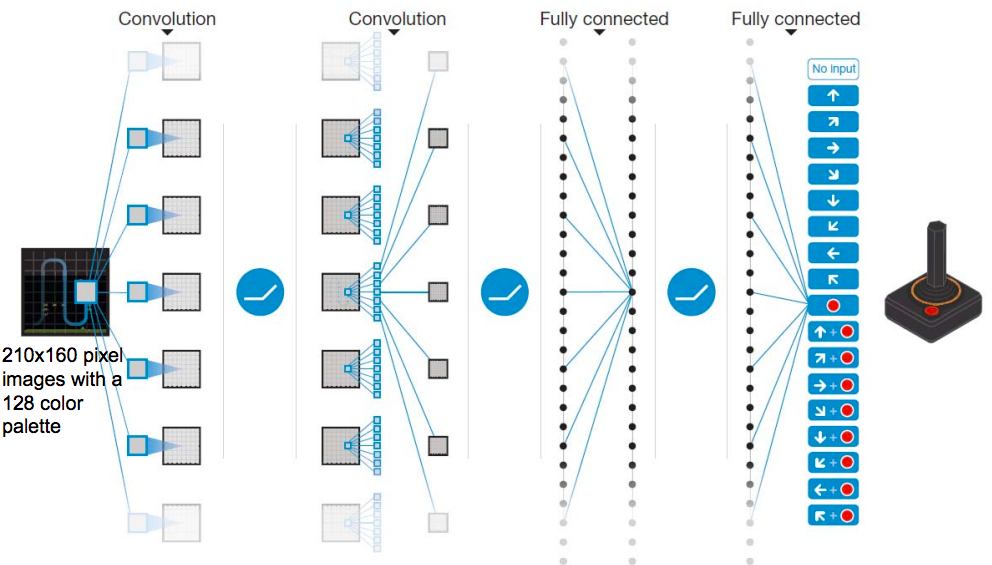
DQN
- 強化学習に深層学習を適用し成功した例
- ゲームの画面自体を入力とするCNNモデルを行動価値関数(Q関数)として利用している。
- CNNでは、入力として状態情報(ある時点におけるゲーム画面の画像)を受け取り、そのとき取りうる各行動の価値を出力する。
- NNで出力される行動価値が真の行動価値に近づくように学習する。
- Experience Replay
- 時系列データは、近い時間のデータが似通ってしまうため、相関性の強い系列となる。
- 強い相関性を持つ入力系列に対して学習を行うと、直近の入力に引きずられてパラメータが修正されるため、過去の入力に対する推定が悪化し、収束性が悪くなる。
- エージェントが経験した状態・行動・報酬・遷移先は一旦メモリに保存される。 損失の計算を行う際には、メモリに保存した値からランダムサンプリングを行う。
L(\theta) = \mathbb{E}_{s,a,r,s'\sim D} \left[ \left( r + \gamma \max_{a'}Q(s',a';\theta) -Q(s,a;\theta) \right)^2 \right]\\
\boxed{
\begin{align}
\mathbb{E}_{s,a,r,s'\sim D} & \mbox{:ランダムサンプリングされたデータを用いて学習する。}\\
r + \gamma \max_{a'}Q(s',a';\theta) & \mbox{:目標値(教師信号)}\\
Q(s,a;\theta) & \mbox{:NNの出力}
\end{align}
}
- Target Q-Networkの固定
- 学習の目標値(教師信号)算出に用いるネットワークと、行動価値Qの推定に用いるネットワークが同じ場合、行動価値関数を更新すると目標値(教師信号)も変化してしまい、学習が不安定になる。
- 学習の目標値の計算に用いる価値関数を固定する。一定期間の学習の間、目標値の計算に用いる価値関数ネットワークのパラメータを固定し、一定周期でこれを 更新することで学習を安定させる。
$r + \gamma \max_{a'}Q(s',a';\theta^-)$ ・・・過去のある時点のパラメータ$\theta^-$を使って行動価値関数$Q$が最大になる行動$a$を求める。
-
報酬のクリッピング
- ゲームの種類によって得点の範囲が異なるため、報酬のスケールがゲームによって異なる。このままだと学習が不安定になる。
- 報酬の値を[-1, 0, 1] の3通りに制限することで学習を安定させる。
-
Huber損失
- 誤差が大きい場合に二乗誤差を使用すると誤差関数の出力が大きくなりすぎて学習が安定しづらい。
\begin{equation}
L_\delta (a) =
\begin{cases}
\frac{1}{2}a^2 & |a|\leqq 1 \\
\delta (|a| - \frac{1}{2}\delta) & \text{上記以外}
\end{cases}
\end{equation}
参考
https://ja.wikipedia.org/w/index.php?title=%E7%A2%BA%E7%8E%87%E7%9A%84%E5%8B%BE%E9%85%8D%E9%99%8D%E4%B8%8B%E6%B3%95
https://en.wikipedia.org/wiki/Autoencoder
- Ilya Sutskever, Oriol Vinyals, Quoc V. Le. Sequence to Sequence Learning with Neural Networks.2014.
- 『ゼロから作る Deep Learning』のリポジトリ
- 『ゼロから作る Deep Learning ❷』のリポジトリ