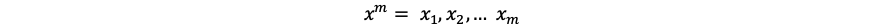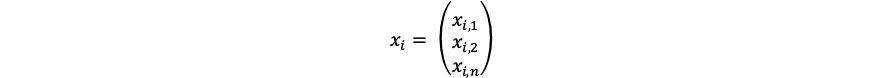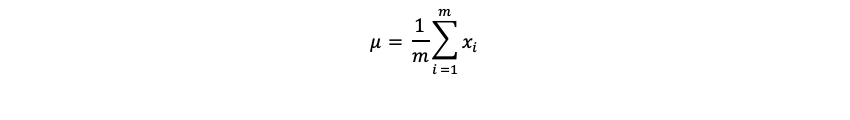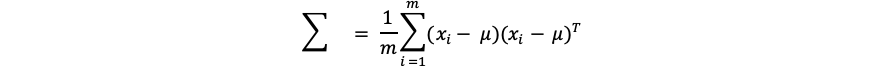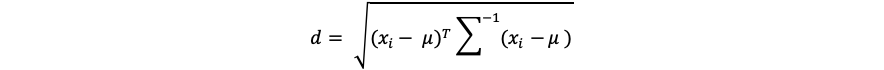はじめに
大学院で受講していた講義で、k-NNを用いて教授と自分の色覚がどの程度似ているのかを算出するプログラムを作成するといった課題がありました。
本記事は、その課題の条件である
k-NNの仕組みを理解するために、機械学習ライブラリを用いることなく実装せよ。
というものにのっとり、進めていきます。
よって、**「こちとら時間がないんじゃあ!!」**という場合(その様なケースが殆ど?)には、
あまり適していないのかもしれません。悪しからず。
間違えている部分がございましたらご指摘のほどよろしくお願い致します!
また、今回Qiita初投稿なので、「わかりにくいんだよっ!こらっ!」ってことがあれば、
ゴリゴリ指摘をいただきたいです。
環境
・python3.6
・macOS Mojave
k-NNとは
k-NNとは、k近傍法のことで、機械学習アルゴリズムの一つです。
また、教師あり学習のクラス分類手法の一つです。
クラス分類時には、あらかじめ学習データが既知で、そのデータの各データ点と、新しく取得した未知のデータとの距離を、近い順にk個算出し、多数決でクラスを推定しています。
以下のページがとても参考になりました。
k_NNでの距離とは
k-NNでは、前項でも述べた様にデータとデータの距離を算出して、クラスの推定を行います。
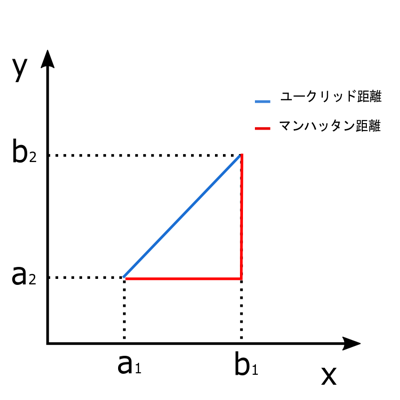
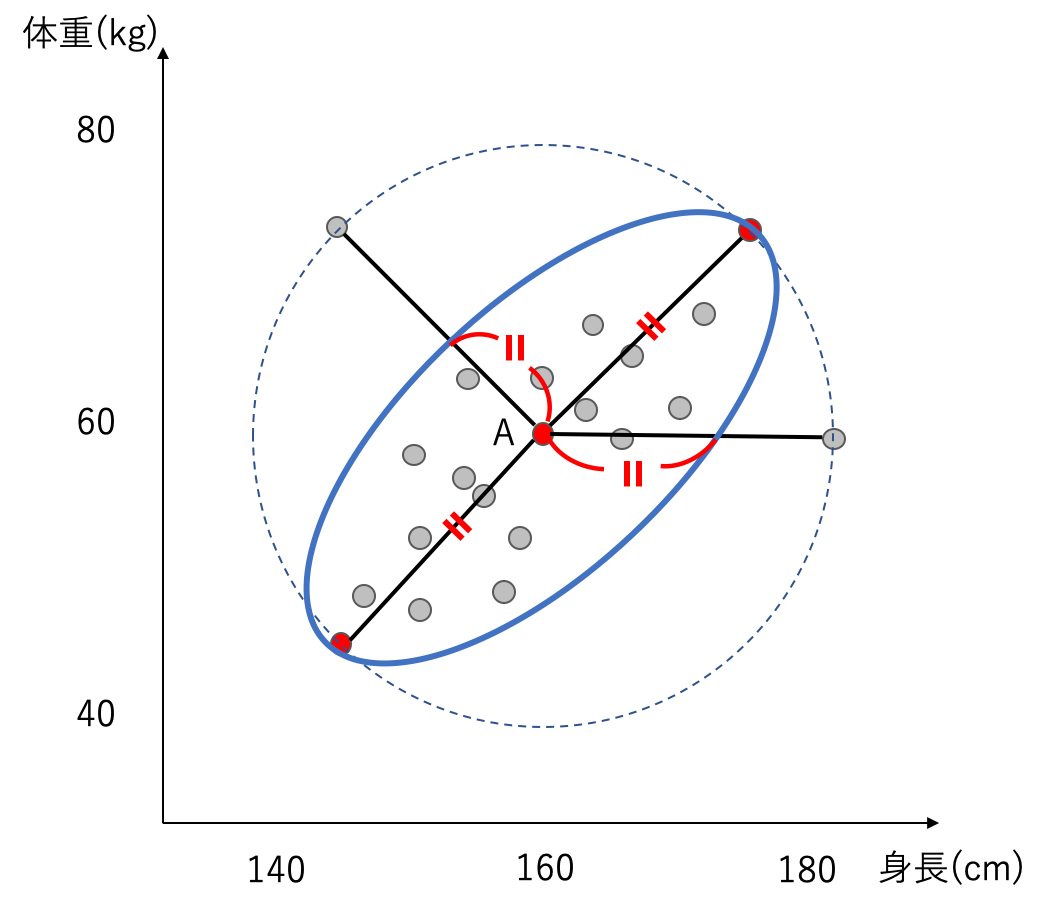
その距離の算出方法として、一般的にはユークリッド距離が用いられることが多い様です。ユークリッド距離とは以下の図の青色の線の部分です。
ユークリッド距離
ユークリッド距離dは以下の式で表されます。
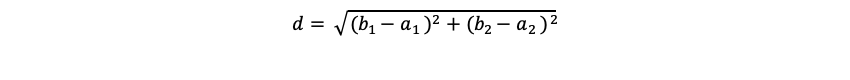
例として、以下の図のような、身長と体重をプロットした平面を考えます。各点は対象とした人々を表しています。平均的なデータとなるAから赤くプロットした点の距離を考えてみると、全て同じ距離を示します。ユークリッド距離は、変数間の相関を考慮しないので、データの集まりから遠く離れている点でも平等に扱います。
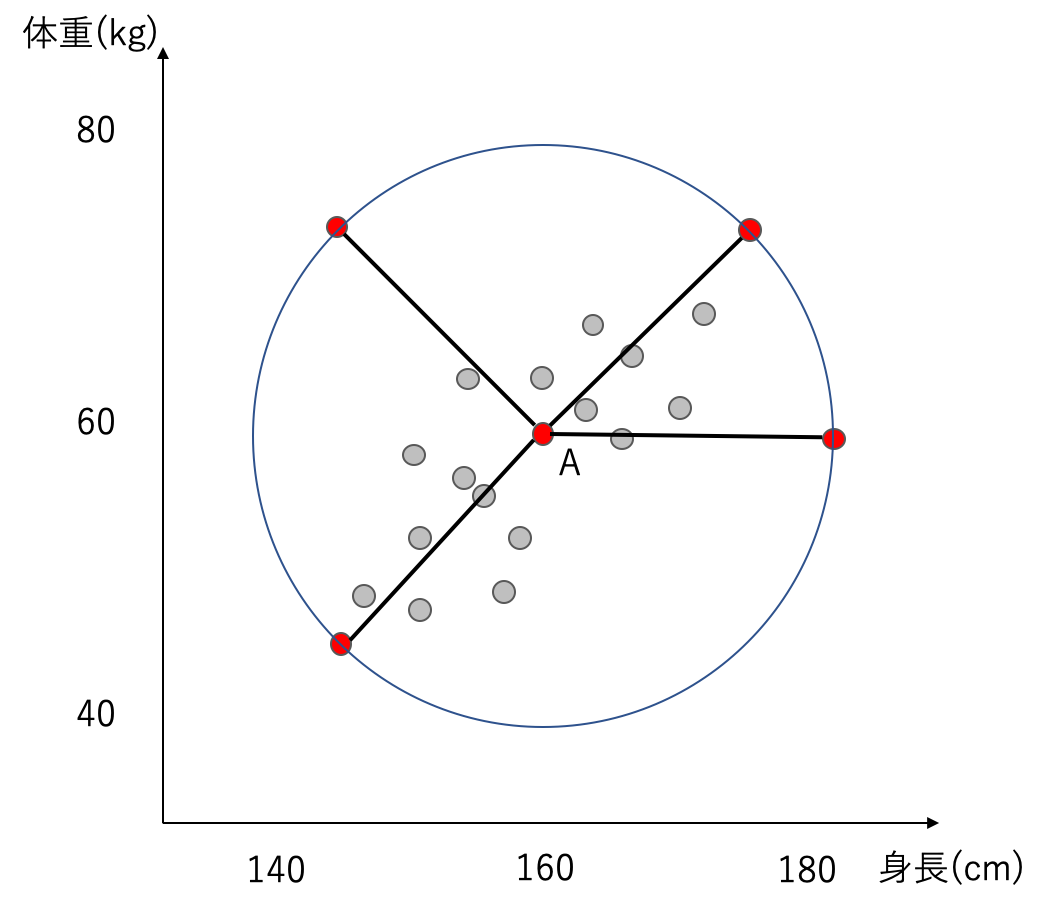
この様な、変数間に相関がある場合は、ユークリッド距離は良い距離とは言えません。
マハラノビス距離
マハラノビス距離を簡単に述べると、「変数間の相関を考慮した距離」です。
仮にデータがn次元でm個あったとすると、得られたデータ列を
として、i番目のデータは、
となります。この時の平均値ベクトルは
となり、分散共分散行列は、
となります。
先ほどの例で考えると、以下の図の様になり、相関が強い方向の距離は、実際の距離よりも相対的に短くなります。
つまり、分散が大きいと、原点からの距離はあまり離れていないと解釈することができ、
分散が小さいと、原点からの距離は大きく離れているということになります。
使用したデータについて
- あらかじめ用意された、**「乱数を用いて生成された緑と青の中間色を提示し、緑と青のどちらの色かを判断した結果をCSVファイルに保存する」**という内容のプログラムを使用し、教授が生成したdata.csvを学習データとして用いる。
- テストデータとして、自らも先のプログラムを使用し、test.csvを生成する。
- 生成されたcsvファイルの中身は、提示された色のRGBの内、GとBの値と、判断されたクラスが各行にデータ毎に記されている。
G, B, Class
310,207,0
170,144,0
196,178,0
126,266,1
176,279,1
.
.
.
合計100個のデータ
実装・前処理
データ読み込み
まずは、作成したdata.csvとtest.csvを読み込みます。
def csv_read(csv_f):
# データ読み込み
df = pd.read_csv(csv_f,header=None)
N = len(df)
T = np.zeros((N,2))
X = np.zeros((N,2))
# for i in N:
for k in range(2):
# G&B
X[:,k] = df[k]
T[:,0] = df[2]
T[:, 1] = [1 if i == 0 else 0 for i in T[:,0]]
X = min_max(X)
return X, T, N
この関数ではXとTとNが返り値として設定されています。それぞれ、GとBの値が入った二次元配列、One hot表現で示されたクラスが入った二次元配列、データの総数となっています。
これを用いて、以下の様にデータを読み込みます。
# 引数はdata.csv
# X0 = 2つの変数のデータが入る2次元配列, T0 = X0のクラスが入る2次元配列 , N0 = 要素数
X0, T0, N0 = csv_read(csv_f[0])
# テストデータが指定されている場合に行う
if len(csv_f) > 1:
# 引数はtest.csv
X1, T1, N1 = csv_read(csv_f[1])
else:
X1, T1, N1 = X0, T0, N0
メイン処理
次に、data.csvの分散共分散行列を求めます。
def covariance_and_inverse(a, b):
"""a,bの異なる変数の共分散をして、逆行列を返す関数"""
co = np.cov(a,b)
return np.linalg.inv(co)
以下の様にして求めます。
# 引数の逆行列が返る
g = covariance_and_inverse(X0[:,0],X0[:,1])
次が、本プログラムの核となる部分です。
k=3~16とし、どのkが一番結果がよくなるのかを確認します。
knn_mah_list = np.zeros((N0,N0))
knn_mah_result = []
TT = np.zeros((N0))
# 最適なKを見つけるため
for k in range(3,16):
for i, t in enumerate(X1):
for j, r in enumerate(X0):
knn_mah_list[i,j] = mah(r - t, g)
# 値が小さい順にk個のインデックスを取得
# それぞれのインデックスのクラスを取得し、合計をとる
k_sum = sum(T0[np.argpartition(knn_mah_list[i,:], k)[:k],0])
# 多数決をし、クラスを決定する
if k_sum / k >= 0.5 :
TT[i] = 1
else:
TT[i] = 0
knn_mah_result.append(np.sum(T1[:,0] == TT))
プログラム中でマハラノビス距離を計算している関数は以下です。
def mah(x, g):
"""マハラノビス距離を返す関数"""
return np.dot(np.dot(np.transpose(x), g), x)
結果の表示部分は以下となっています。
"""結果表示部"""
print("正解率は{0}%です。".format(max(knn_mah_result) / N0 *100))
print("最も正解率の高いkは{0}です。".format(knn_mah_result.index(max(knn_mah_result))+3))
print(knn_mah_result)
x = [3,4,5,6,7,8,9,10,11,12,13,14,15]
plt.plot(x,knn_mah_result)
plt.xlabel('k')
plt.ylabel('accuracy rate')
plt.show()
そして!たくさんの方が気になりまくりであろう**(絶対なってない)**、
私と教授の色覚の類似度は、
k=10の時に、95%となっております!!!
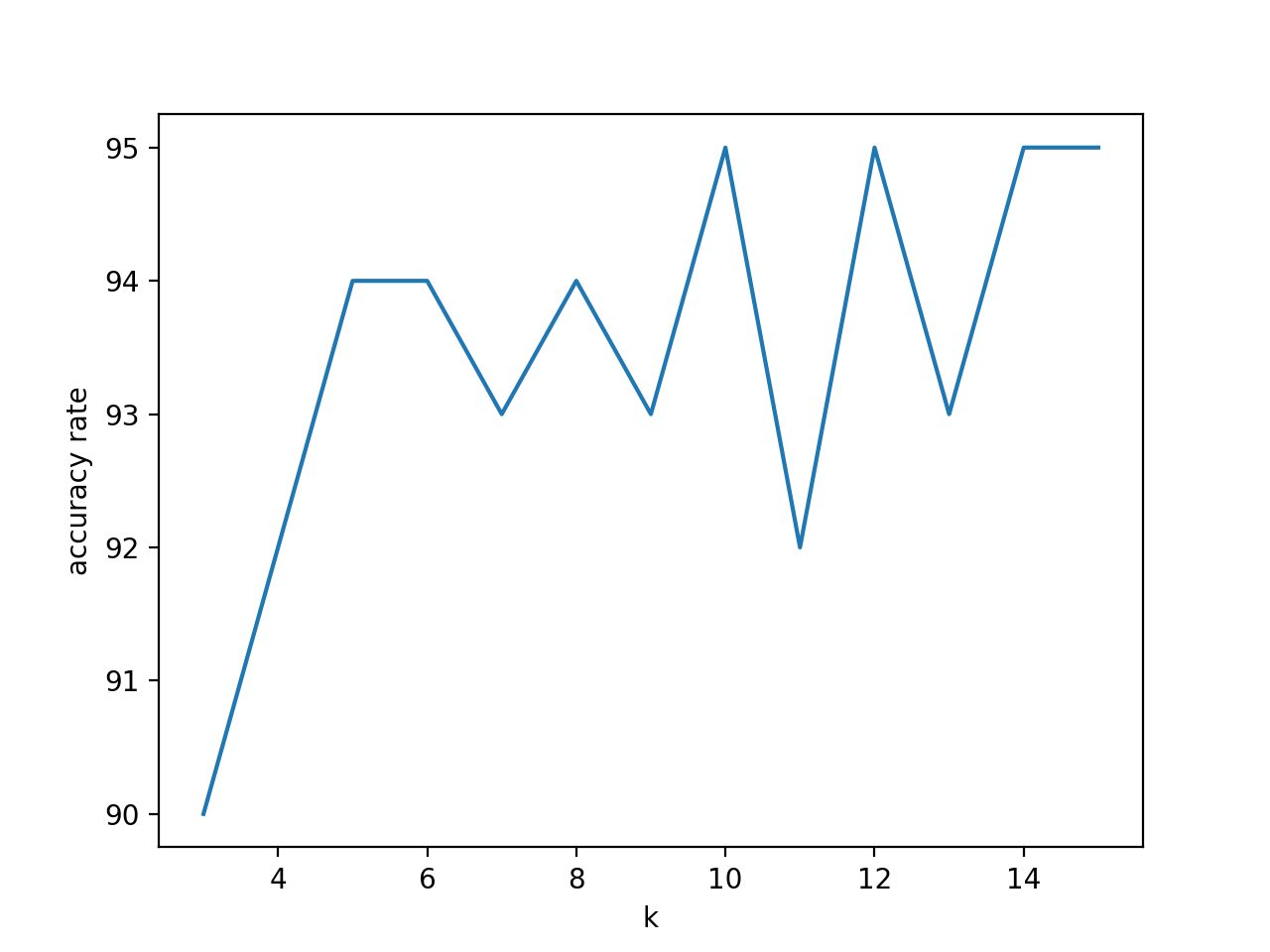
そして、本記事のはじめに表示されている画像は、一致しなかった色の一例です。
みなさんは、何色に見えましたか?コメントお待ちしております!
私は、左が青で、右が緑と判定していました。
プログラム全文
import numpy as np
import matplotlib.pyplot as plt
import sys
import os.path
from study_machine_learning_calc import covariance_and_inverse, mah, csv_read
def knn_mah(*csv_f):
"""マハラノビス距離を用いたk近傍法"""
# X0 = 2つの変数のデータが入る2次元配列, T0 = X0のクラスが入る2次元配列 , N0 = 要素数
X0, T0, N0 = csv_read(csv_f[0])
# テストデータが指定されている場合に行う
if len(csv_f) > 1:
X1, T1, N1 = csv_read(csv_f[1])
else:
X1, T1, N1 = X0, T0, N0
# 引数の逆行列が返る
g = covariance_and_inverse(X0[:,0],X0[:,1])
knn_mah_list = np.zeros((N0,N0))
knn_mah_result = []
TT = np.zeros((N0))
#最適なKを見つけるため
for k in range(3,16):
for i, t in enumerate(X1):
for j, r in enumerate(X0):
knn_mah_list[i,j] = mah(r - t, g)
# 値が小さい順にk個のインデックスを取得
# それぞれのインデックスのクラスを取得し、合計をとる
k_sum = sum(T0[np.argpartition(knn_mah_list[i,:], k)[:k],0])
# 多数決をし、クラスを決定する
if k_sum / k >= 0.5 :
TT[i] = 1
else:
TT[i] = 0
knn_mah_result.append(np.sum(T1[:,0] == TT))
"""結果表示部"""
print("正解率は{0}%です。".format(max(knn_mah_result) / N0 *100))
print("最も正解率の高いkは{0}です。".format(knn_mah_result.index(max(knn_mah_result))+3))
print(knn_mah_result)
x = [3,4,5,6,7,8,9,10,11,12,13,14,15]
plt.plot(x,knn_mah_result)
plt.xlabel('k')
plt.ylabel('accuracy rate')
plt.show()
if __name__ == "__main__":
args = sys.argv
# 学習データとテストデータが引数で設定されている場合
if len(args) == 3:
if os.path.splitext(args[1])[1] == ".csv" or os.path.splitext(args[2])[1] == ".csv":
knn_mah(args[1], args[2])
else:
print("csvファイルでお願い申す。")
# 学習データのみの場合
elif len(args) == 2:
if os.path.splitext(args[1])[1] == ".csv":
knn_mah(args[1])
else:
print("csvファイルでお願い申す。")
elif len(args) == 1:
print("学習させたいデータのファイルを引数に設定してくだせえ。")
else:
print("学習させたいデータのファイルは1つにしてくだせえ。")
def csv_read(csv_f):
# データ読み込み
df = pd.read_csv(csv_f,header=None)
N = len(df)
T = np.zeros((N,2))
X = np.zeros((N,2))
# for i in N:
for k in range(2):
# G&B
X[:,k] = df[k]
T[:,0] = df[2]
T[:, 1] = [1 if i == 0 else 0 for i in T[:,0]]
X = min_max(X)
return X, T, N
def covariance_and_inverse(a, b):
"""a,bの異なる変数の共分散をして、逆行列を返す関数"""
co = np.cov(a,b)
return np.linalg.inv(co)
def mah(x, g):
"""マハラノビス距離を返す関数"""
return np.dot(np.dot(np.transpose(x), g), x)