はじめに
果物は食べる前にしっかり冷やしておきたいですが、どのくらい待っていれば良いのでしょうか?。あるサイトでは、「(メロンを)冷蔵庫に移すのは、実際に食べる2~3時間前の範囲が理想です」と書いてあります。しかしながら、大きいメロンもあれば小さいメロンもあり、大きさによって冷やすべき時間も変わってくるハズです。本記事では、2~3時間という目安時間の妥当性を検討しつつ、任意の大きさの場合について冷やす時間の目安を非定常熱伝導方程式を用いて検討してみたいと思います。*お肉の焼き方について、同様の検討を行っている方がいらっしゃいました。
条件
非定常熱伝導方程式を球座標について検討した情報は自分が調べた限りだと見当たらなったことから、解析解と数値計算の両方を用いて計算を行い、それらが一致することを確かめることで計算結果の正確さを担保していきたいと思います。
計算に用いた物理量や各種条件は以下の通りです。果物の8~9割が水分であるため、いくつかは代替として水の物理量を用いています。
密度 1000 kg/m^3 (水)
比熱 3952 J/(kgK) (甘露メロン)データ元
熱伝導率 0.582 W/mK(水)
初期条件 20度 (室温)
境界条件 0度 (計算簡略化の為、実際の冷蔵庫温度よりも少し低めに設定)
解析解の導出
まずは境界条件及び初期条件に基づいて非定常熱伝導方程式を解いていきます。変数分離とフーリエ級数を用いて解を求めています。解法は調べても出てこなかったことから手計算したため、どこか怪しい個所があったら是非コメントをお願い致します。
非定常熱伝導方程式の一般形($D=\frac{\kappa}{\rho c}$)
$\frac{\partial u}{\partial t}=D\nabla^2 u$
境界条件と初期条件。
$B.C. u(R,t)=0 $
$I.C. u(r,0)=T_0 $
温度の対称性を考慮すると、支配方程式は以下の形となる。
$\frac{\partial u}{\partial t}=D\frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial u}{\partial r})$
変数分離法を用いる為、u(r,t)がrとtのみの関数の積で表されると仮定する。
$u=R(r)T(t)$
微分方程式へ代入して解く。
$R(r)\frac{1}{D}\frac{dT}{dt}=T(t)\frac{1}{r^2}\frac{d}{dr}(r^2\frac{dR}{dr}) $
両辺をR(r)T(t)で割る。
$\frac{1}{DT}\frac{dT}{dt}=\frac{1}{R}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{dR}{dr})$
左辺はtのみ、右辺はtのみであるので、これらは定数となる。その定数の値を$-\alpha^2$と置く。
$\frac{1}{DT}\frac{dT}{dt}=-\alpha^2 $...(1)
$\frac{1}{R}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{dR}{dr})=-\alpha^2 ...(2)$
(1)のtについての式から解く。
$\frac{1}{DT}\frac{dT}{dt}=-\alpha^2$
$\frac{dT}{T}=-\alpha^2 Ddt$
$T=C\exp(-\alpha^2Dt)...(3)$ (Cは定数)
(2)については、変数変換を経て解く。
$\frac{1}{R}\frac{1}{r^2}\frac{d}{dr}(r^2\frac{dR}{dr})=-\alpha^2$
整理すると以下の式を得る。
$r^2R''+2rR'+\alpha^2 r^2R=0$
$R=\frac{v}{r}$と置いて、微分を計算する。
$R''=\frac{v''}{r}-\frac{2v'}{r^2}+\frac{2u}{r^3}$
$R'=\frac{v'}{r}-\frac{v}{r^2}$
以上を代入して整理すると、以下の式を得る。
$v''+\alpha^2v=0$
この微分方程式の解は三角関数となるので、AとBを定数として、以下の解を得る。
$v=A\cos(\alpha r)+B\sin(\alpha r)$
$r \to 0$でRの値を有限とする為に、$A=0$とする。($\lim_{\theta \to 0} \frac{\sin(\theta)}{\theta}=1$なので$B$の方は有限値に留まるハズ)
よって、$R$は以下の形で書くことができる。
$R=\frac{B\sin(\alpha r)}{r}...(4)$
(3)と(4)より、$u$は以下の形を取る。
$u=\frac{B\sin(\alpha r)}{r}\exp(-\alpha^2 Dt)$
$u(R,t)=0$を代入する。
$\frac{B\sin(\alpha R)}{R}\exp(-\alpha^2 Dt)=0$
$\sin(\alpha R)=0$
これを満たす為には、以下の条件を取る。
$\alpha=\frac{n\pi}{R}$
よって、一般解は重ね合わせで表現できる。
$u=\sum_{n=1}^\infty \frac{C_n \sin(\frac{n\pi r}{R})}{r} \exp(-(\frac{n\pi}{R})^2 Dt)$
$u(r,0)=T_0$より
$\sum_{n=1}^\infty \frac{C_n \sin(\frac{n\pi r}{R})}{r}=T_0$
$\sum_{n=1}^\infty C_n \sin(\frac{n\pi r}{R})=T_0 r$
これはフーリエ級数展開の一例であるので、$B_n$は以下の様に求まる
$B_n=\frac{2T_0}{n\pi}R(-1)^{n+1}$
以上より、$u$は以下の形で表現できる。
$u=\sum_{n=1}^{\infty}\frac{2T_0}{n\pi}R(-1)^{n+1}\frac{\sin(\frac{n\pi r}{R})}{r}\exp(-(\frac{n\pi}{R})^2 Dt)$
解析解に基づいた温度計算
解析解が求まったので、温度計算を行っていきましょう。中心部分($r=0$)は扱えない為、中心から1 mmの地点での温度変化を追いかけていきます。ざっくりですが5度ほどを食べごろの
温度と考えて、中心から1 mmの距離が5度を下回る時間を教えてくれる関数を実装します。
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm
from scipy.sparse import csr_matrix
# 第500 項までの和で解析解を近似
def thermal_conduction(t,R):
temp=0
for n in range(1,500):
nth_term=(2*T0*R/(n*np.pi))*((-1)**(n+1))*(np.sin(n*np.pi*r/R)/r)*np.exp(-((n*np.pi/R)**2)*(kappa/(ro*c))*t)
temp=temp+nth_term
return temp
def tabegoro_calculator(f,R):
t=np.linspace(1,3600*15,300)
for time in t:
if f(time,R)<5:
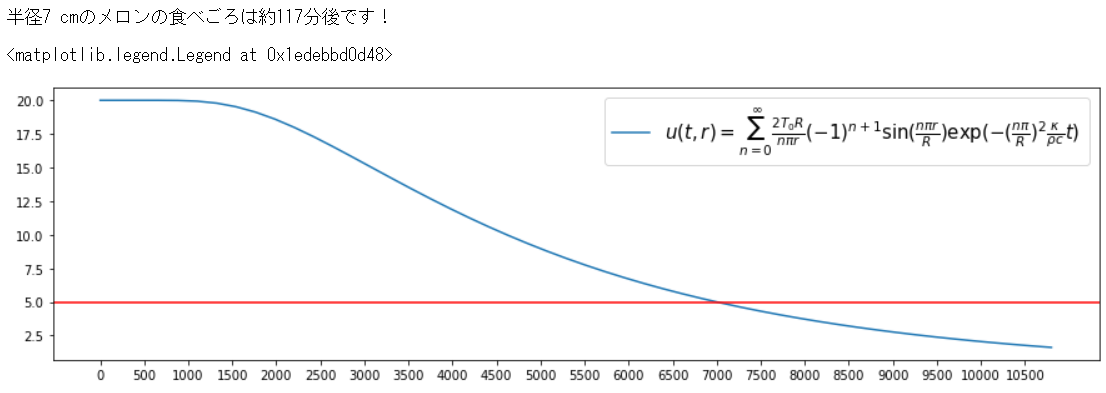
print(f"半径{int(R*100)} cmのメロンの食べごろは約{int(time/60)}分後です!")
endtime=time+3600
break
else:
continue
半径7 cmのメロンを想定して計算してみた結果です。
ro=1000
c=3952
kappa=0.582
T0=20
r=0.001
endtime=3
tabegoro_calculator(thermal_conduction,R=0.07)
t=np.linspace(1,3600*endtime)
fig=plt.figure(figsize=(15,4))
ax=fig.subplots()
ax.plot(t,[thermal_conduction(t,R=0.07) for t in t],
label=r"$u(t,r)=\sum_{n=0}^\infty \frac{2T_{0}R}{n\pi r}(-1)^{n+1} \sin(\frac{n\pi r}{R})\exp(-(\frac{n\pi}{R})^2\frac{\kappa}{\rho c}t)$ ")
ax.axhline(5,color="red")
ax.set_xticks(np.arange(0, 3600*endtime, 500))
ax.legend(fontsize=15)
117分≒約2時間となりました!一般的に冷やす時間の目安とされている2時間~3時間と概ね一致します。若干時間が短いのは、水の物理量を代替として用いていることや、より熱を通しにくいと考えられる果皮の影響を考慮していない事が原因として考えられます。本来は多層構造をしている果物の構造を均一に単純化しているのも、原因の一つかもしれません。
数値計算による検算
解析解による温度計算結果は一般的な冷やす目安時間と類似した値となりましたが、偶然による一致である可能性も考えられます。そのため、数値計算によっても同様の結果が出るかを確かめてみました。
数値計算には様々な方法がありますが、数値計算については大昔に講義でExcelを使った計算をちょっとやったきりなので、今回は最もシンプルな差分法(陽解法)を用いたいと思います。
微分方程式の数値計算では、連続的な方程式を離散化して計算を進めていきます。今回は偏微分方程式ですので、時間についての微分と空間についての微分で別々の刻み幅を使って離散化していきます。以下では$i$は時間のインデックス、$j$は空間のインデックスとなっています。
$\frac{\partial u}{\partial t}\simeq\frac{u_j^{i+1}-u_j^i}{k}$
$\frac{\partial u}{\partial r}\simeq\frac{u_{j+1}^{i}-u_j^i}{h}$
$\frac{\partial^2 u}{\partial r^2}\simeq\frac{u_{j+1}^{i}-2u_j^i+u_{j-1}^i}{h^2}$
これらを支配方程式へと代入して整理すると、以下のベクトルの内積の形へまとめることができます。
$u_j^{i+1}=\frac{kD}{h^2}[1,\frac{h^2}{kD}-\frac{2}{j}-2,\frac{2}{j}+1][u_{j-1}^i,u_j^i,u_{j+1}^{i}]^T$
このことを利用すると、系の時間発展は疎行列の掛け算で考えることができます。pythonではscipyのsparse matrixを利用することで、高速で疎行列の演算を行う事ができます。これによって、通常の方法では20分以上かかる計算を、最速で20秒弱まで短縮することが出来ました。数値計算を行う上で必要となった球体中心($r=0$)における境界条件は、温度分布の対称性を考え、温度の$r$に対する一回微分の値が中心でゼロとなるものとしています。
# 疎行列を用いた計算
R=0.07
k=0.01 #時間の刻み幅は 0.01 s
h=0.0001 #空間の刻み幅は 0.00001 m
n=int(R/h) #空間計算グリッド数
Tf=0.0 #境界条件
T0=20.0 #初期条件
init=np.array([T0 for p in range(n)])
D=kappa/(ro*c)
A=np.zeros((n-2,n))
for j in range(1,n-1):
A[j-1,j+1]=2/j+1
A[j-1,j]=(h**2)/(k*D)-2/j-2
A[j-1,j-1]=1
A=csr_matrix((k*D/(h**2))*A)
def forward_calc_2(ith_arr):
i_plus1_th_arr=A*ith_arr
i_plus1_th_arr=np.append(i_plus1_th_arr,Tf)
i_plus1_th_arr=np.append(i_plus1_th_arr[1],i_plus1_th_arr)
return i_plus1_th_arr
time=3 #3時間分の計算
init=np.array([T0 for p in range(n)])
values=[init]
for N in tqdm(range(int(time*3600/k))):
ith_arr=values[N]
i_plus1_th_arr=forward_calc_2(ith_arr)
values.append(i_plus1_th_arr)
各時刻における温度分布を表示してみます。
fig=plt.figure(figsize=(15,4))
ax=fig.subplots()
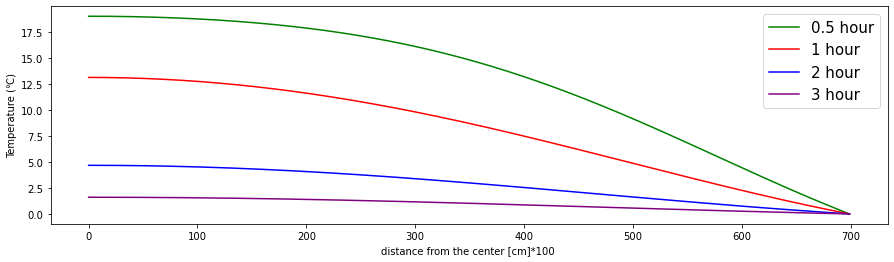
ax.plot(values[int(1800/k)],label="0.5 hour",color="green")
ax.plot(values[int(3600/k)],label="1 hour",color="red")
ax.plot(values[int(7200/k)],label="2 hour",color="blue")
ax.plot(values[int(10800/k)],label="3 hour",color="purple")
ax.set_xlabel("distance from the center [cm]*100 ")
ax.set_ylabel("Temperature (℃)")
ax.legend(fontsize=15)
上記の出力結果より、3時間でメロンの全体が冷えている様子が分かります。
半径7 cm、中心からの距離1 mmの地点における温度変化の値を比較することで、数値計算の結果と、解析解の結果を比較してみましょう。
endtime=3
t=np.arange(0,3600*endtime)
fig=plt.figure(figsize=(15,4))
ax=fig.subplots()
ax.plot(t,[thermal_conduction(t,R=0.07) for t in tqdm(t)],
label=r"$u(t,r)=\sum_{n=0}^\infty \frac{2T_{0}R}{n\pi r}(-1)^{n+1} \sin(\frac{n\pi r}{R})\exp(-(\frac{n\pi}{R})^2\frac{\kappa}{\rho c}t)$ ")
tempChange_at_core=[values[T][int(r/h)] for T in tqdm(range(int(time*3600/k)))]
t=np.arange(0,len(tempChange_at_core),1)
ax.plot(t*k,tempChange_at_core,label="Numerical calculation result",color="red",linestyle="dotted")
ax.set_xlabel("time [s]")
ax.set_ylabel("Temperature (℃)")
ax.legend(fontsize=15)
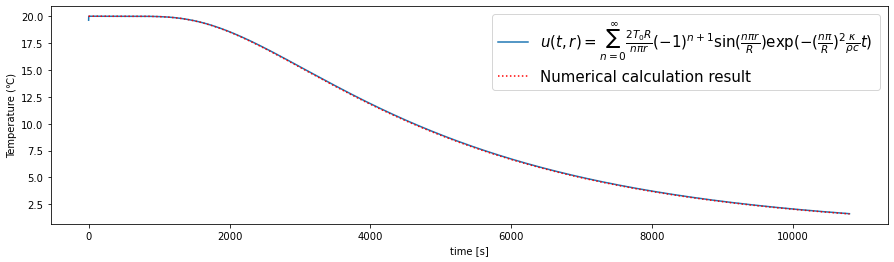
上記の結果から、解析解による温度変化の計算結果と、数値計算の結果がほぼ一致していることが分かります。
最後に
本記事では、非定常熱伝導方程式の解析解の導出とその結果を用いた温度の時間変化の計算に加えて、偏微分方程式の差分化と疎行列を用いた計算高速化、解析解の結果との比較を行いました。解析解の強みは一度手で解いてしまえば実装が行いやすいことですが、初期条件や境界条件を変える度に計算をやり直さなくてはいけません。対して数値計算の場合には、少し計算を工夫することで計算速度の問題を低減でき、また境界条件や初期条件の変更が容易です。しかしながら、時間や空間の刻み幅を荒くすると途端に解が不安定となってしまったため、調整がやや難かったです。
メロンを美味しく食べたいという願望から生まれた記事でしたが、もし楽しく読んでいただけた方がいらっしゃったら幸いです。それでは、よきフルーツライフを!