はじめに
GHZ状態とは
にもある通り、
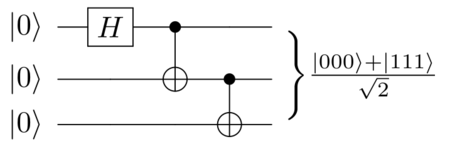
こんな感じで、利用量子ビットについてすべて0状態と、全て１の状態の重ね合わせ状態です。
この、GHZの作成回路には、なにやらバリエーションがありそうなので、列挙してみたいと思います。
（あまり、内容の無い記事で恐縮です。）
また、他の量子コンピュータ関係の他の記事は、下記で紹介しています。
$$
% basic braket
\newcommand{\bra}[1]{\left\langle #1 \right|}
\newcommand{\ket}[1]{\left| #1 \right\rangle}
\newcommand{\bracket}[2]{\left\langle #1 \middle| #2 \right\rangle}
\newcommand{\ketbra}[2]{\left| #1 \right\rangle \left\langle #2 \right|}
\newcommand{\ketbraket}[3]{\left| #1 \right\rangle \left\langle #2 \middle| #3 \right\rangle}
% small-size
\newcommand{\bras}[1]{\left\langle {\scriptsize #1} \right|}
\newcommand{\kets}[1]{\left| {\scriptsize #1} \right\rangle}
\newcommand{\brackets}[2]{\left\langle {\scriptsize #1} \middle| {\scriptsize #2} \right\rangle}
\newcommand{\ketbras}[2]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \right|}
\newcommand{\ketbrakets}[3]{\left| {\scriptsize #1} \right\rangle \left\langle {\scriptsize #2} \middle| {\scriptsize #3} \right\rangle}
% Matrix
\newcommand{\tate}[2]{\begin{bmatrix} #1 \ #2 \end{bmatrix}}
\newcommand{\yoko}[2]{\begin{bmatrix} #1 & #2 \end{bmatrix}}
\newcommand{\mtrx}[4]{\begin{bmatrix} #1 & #2 \ #3 & #4 \end{bmatrix}}
$$
GHZ状態はどんな状態？
000と111の重ね合わせ
下記は３量子ビットですので、3ビットともに0の$\ket{000}$と、3ビットともに1の$\ket{111}$の重ね合わせとなっています。
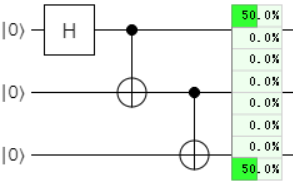
Quirkで見てみるとこんな感じで、000と111の重ね合わせになっています。
余談（均等重ね合わせ）
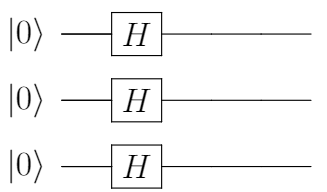
では、余談ですが、これはどうでしょう？
これは、下記8個の状態の均等な重ね合わせなので、GHZ状態ではありません。
\ket{\psi} = \frac{1}{2\sqrt{2}}
\left(
\ket{000} + \ket{001} + \ket{010} + \ket{011}
+ \ket{100} + \ket{101} + \ket{110} + \ket{111}
\right)
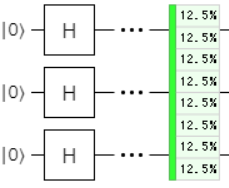
Quirkで見てみるとこんな感じで、8状態の均等な重ね合わせになっています。
Nビットでは
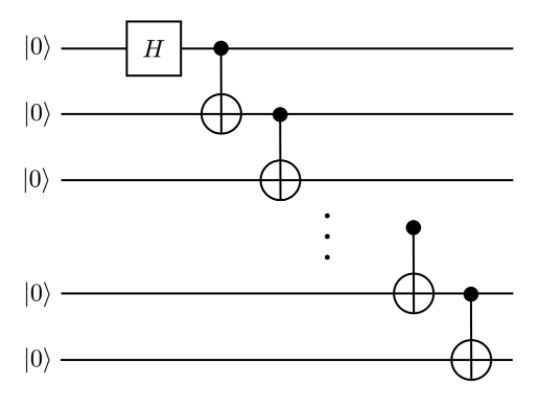
Nビットに対しては1、
\ket{GHZ} = \frac{1}{\sqrt{2}} \left(\ket{0}^{\otimes N} + \ket{1}^{\otimes N} \right)
となり、こんな感じで連鎖的に$Cnot$を適用することで、Nビットの$GHZ$状態が作成できます
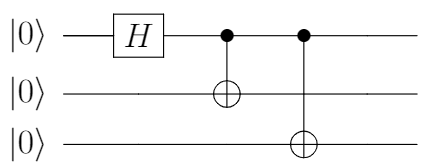
基本形？
これが、一番一般的な形かと思うのですが、この回路でGHZ状態になるかを確認しておきましょう。
\displaylines{
\ket{000}
\xrightarrow{H_1}
\frac{1}{\sqrt{2}}\left( \ket{0} + \ket{1} \right) \otimes \ket{00}
\\
\xrightarrow{Cnot_{12}}
\frac{1}{\sqrt{2}}\left( \ket{000} + \ket{110} \right)
\\
\xrightarrow{Cnot_{23}}
\frac{1}{\sqrt{2}}\left( \ket{000} + \ket{111} \right)
}
なお、Quirkで状態が確認できるようリンクしておきます
変形１
当たり前ではあるのですが、これでもGHZ状態が作れます。
数式で確認すると、上記式の最後の矢印の$Cnot_{23}$が$Cnot_{13}$になりますが、
制御ビットが、1ビット目でも2ビット目でもどちらでも1となっているので結果は変わりません。
\displaylines{
\ket{000}
\xrightarrow{H_1}
\frac{1}{\sqrt{2}}\left( \ket{0} + \ket{1} \right) \otimes \ket{00}
\\
\xrightarrow{Cnot_{12}}
\frac{1}{\sqrt{2}}\left( \ket{000} + \ket{\color{red}{11}0} \right)
\\
\xrightarrow{\color{red}{Cnot_{13}}}
\frac{1}{\sqrt{2}}\left( \ket{000} + \ket{111} \right)
}
なお、Quirkで状態が確認できるようリンクしておきます
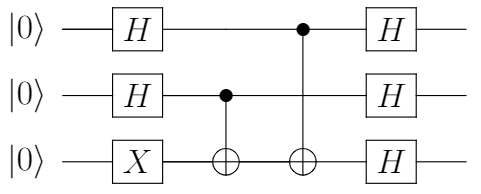
変形２
こんなのでも、GHZ状態が作れます。
計算過程は、こちらの記事に分かりやすく解説されているのでリンクさせていただきます。
なお、Quirkで状態が確認できるようリンクしておきます
まとめ
見つけたバリエーションとしては、３パターンでした。
いずれの回路も、結果は下記のように000と111の重ね合わせでした。1
\ket{GHZ} = \frac{1}{\sqrt{2}} \left( \ket{000} + \ket{111} \right)
| 回路図 | |
|---|---|
| 基本形? |  |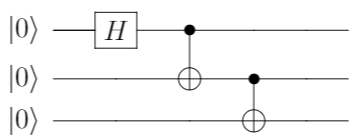
| 変形１ |  |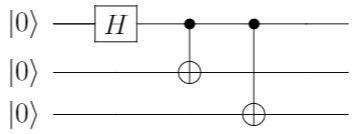
| 変形２ | 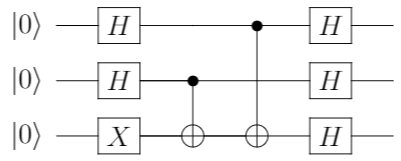 |