はじめに
音声分析におけるスペクトログラムを得るまでに必要な知識をまとめた。
具体的には以下の用語の意味・関係をまとめた。
- フーリエ変換 (FT: Fourier Transform)
- 高速フーリエ変換 (FFT: Fast Fourier Transform)
- 短時間フーリエ変換 (STFT: Short-Time Fourier Transform)
- スペクトル・周波数スペクトル (Spectrum)
- スペクトログラム (Spectrogram)
フーリエ変換とは (FT: Fourier Transform)
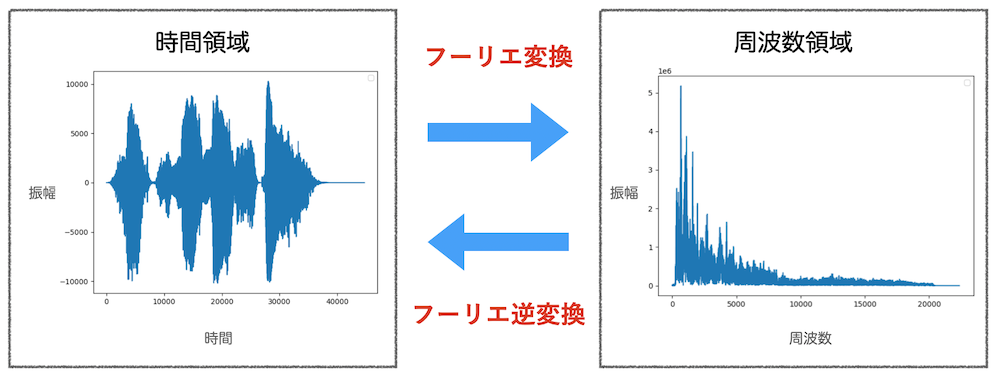
フーリエ変換は時間領域(wavファイルのような横軸を時間、縦軸を振幅としたもの)の値を周波数領域(横軸を周波数、縦軸を振幅としたもの)に変換する手法の1つ。
機械学習等で音声を扱うときは、時間領域のままでは上手く扱うことができず、周波数領域の値を使う方が好ましい。
時間領域から周波数領域に変換することを、まとめてフーリエ変換と言っていることが多いが厳密には違う。
時間領域から周波数領域の変換は、連続値と離散値の組み合わせで4種類あり、フーリエ変換はその1つである。
| 時間領域 | 周波数領域 | 変換手法 |
|---|---|---|
| 連続 | 離散 | フーリエ級数展開 |
| 連続 | 連続 | フーリエ変換 |
| 離散 | 連続 | 離散時間フーリエ変換 |
| 離散 | 離散 | 離散フーリエ変換 (DFT: Discrete Fourier Transform) |
コンピュータでは基本的に離散値しか扱えないため、音声分析に使用されるのは主に離散フーリエ変換となる。DFTという略称でかかれることも多い。
この記事の以下でも、一般化のため、時間領域から周波数領域の変換を総称してフーリエ変換と表現する。
高速フーリエ変換とは (FFT: Fast Fourier Transform)
高速フーリエ変換(こうそくフーリエへんかん、英: fast Fourier transform, FFT)は、離散フーリエ変換(英: discrete Fourier transform, DFT)を計算機上で高速に計算するアルゴリズムである。
引用:高速フーリエ変換 - Wikipedia (https://ja.wikipedia.org/wiki/高速フーリエ変換)
高速フーリエ変換は、離散フーリエ変換をコンピュータで高速に計算する手法である。得られる値は離散フーリエ変換と同じ。なので、python等のライブラリを使ってフーリエ変換を行う場合は、基本的に高速フーリエ変換を用いる。FFTという略称でかかれることも多い。
短時間フーリエ変換とは (STFT: Short-Time Fourier Transform)
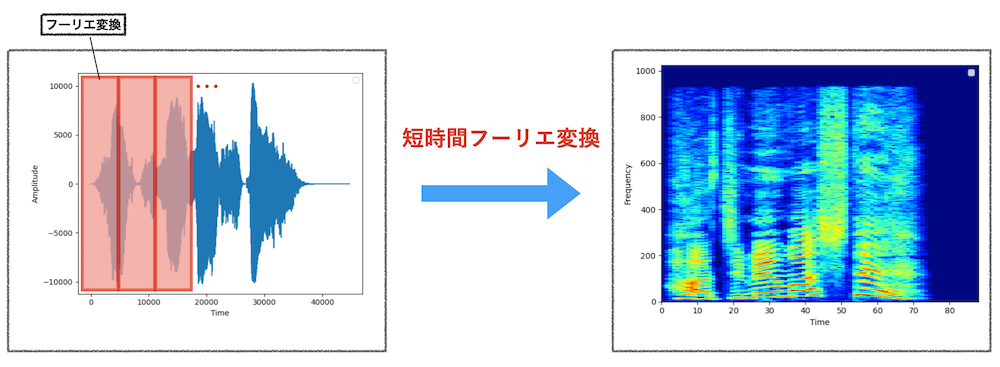
フーリエ変換は時間領域全体に対して適用されるため、フーリエ変換後の周波数領域に時間情報はない。
ただ、音声分析では「こんにちは」という文章全体の周波数情報ではなく「k,o,n,n,n,i,c,h,i,w,a」といった音素ごとの周波数情報を得ることが重要である。
短時間フーリエ変換では時間領域を区間的にフーリエ変換する。それにより、時間変化する音声の分析を行うことが可能になる。短時間フーリエ変換後の値は「時間・周波数・振幅」の三次元の値になる。以下の図では見やすさのために振幅をdbに変換して表示している。
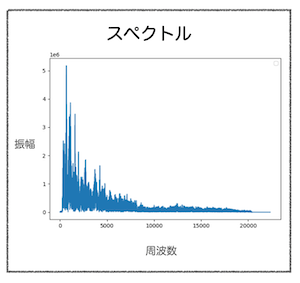
スペクトル・周波数スペクトルとは (Spectrum)
音声分析では、音声をフーリエ変換したものをスペクトル、または周波数スペクトルと呼ぶ。簡単に言うと以下の図のこと。音声をスペクトルで分析することをスペクトル分析という。英語ではSpectrumなので、スペクトラムやスペクトラル分析と言うこともある。
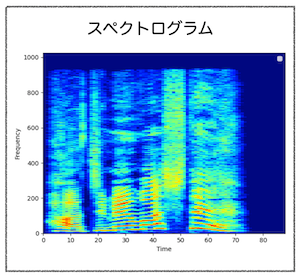
スペクトログラムとは (Spectrogram)
音声分析では、音声を短時間フーリエ変換したものをスペクトログラムと呼ぶ。簡単に言うと以下の図のことである。
まとめ
音声分析では、似たような言葉で同じ意味・違う意味のものが多く存在し、混乱したのでまとめてみた。他にもケプストラムやメルスペクトラムといった専門用語もあるので、次はその辺りもまとめていきたい。
参考文献
離散フーリエ変換(DFT)の仕組みを完全に理解する
https://qiita.com/TumoiYorozu/items/5855d75a47ef2c7e62c8