Rubyでミンコフスキー距離

##ITP1_10_D
AOJより、ミンコフスキー距離を算出する問題

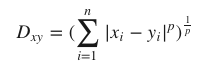
文系の僕には式を見ても何も理解出来ませんでした。
Σなんて高校数学以来触ってすらない・・・。
Σを用いない計算式がググってもなかなか見つからずに困ったので備忘録用に。

##結論

n = gets.to_i
a=gets.split.map &:to_i
b=gets.split.map &:to_i
c=n.times.map{|i|(a[i]-b[i]).abs}
p c.sum
p c.map{|i| i**2}.inject(:+)**0.5
p c.map{|i| i**3}.inject(:+)**(1/3.to_f)
p c.max

##p=1~2までのそれぞれの距離の定義

#マンハッタン距離
Dxy=|x1−y1|+|x2−y2|+...+|xn−yn|

#ユークリッド距離
Dxy=√(|x1−y1|)**2+(|x2−y2|)**2+...+(|xn−yn|)**2)

#チェビシェフ距離
Dxy=maxni=1(|xi−yi|)

問題文に付属していた公式が上記。
p=1,2の場合は理解出来るがp=3の事例は見当たらずチェビシェフ距離の公式に至っては何を意味してるのかが分からない。
Wikipediaよりチェビシェフ距離とはチェス盤の距離らしいので、なんだ(|x2-x1|,|y2-y1|)のことかと解決。
今回の場合では絶対値の最大値を取ってあげれば解決。

##p=3の距離の定義

Dxy=(|x1−y1|)**3+(|x2−y2|)**3+...+(|xn−yn|)**3)**(1/3)

ググったところ、p=2のケースに１足して考える模様。
√は**(1/2)とも受け取れるので、+1して**(1/3)にするようです。

##追記
@scivola さんの投稿 ミンコフスキー距離を絵にしてみた にて絵にして頂きました、光栄の限りです・・。