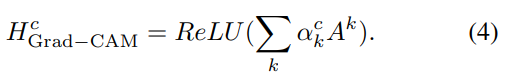【論文読み】深層距離学習でGrad-CAM

通常の画像分類問題などで「判断根拠の可視化」を行う場合、Grad-CAMが良く用いられます。
これはGrad-CAMが一番分かりやすく、過不足なく可視化してくれるためだと思われます。

本稿で紹介する論文は、このGrad-CAMを深層距離学習に適用できるようにしたものです。

※本稿の図は、基本的に「Adapting Grad-CAM for Embedding Networks」より引用しています。

#概要

• 深層距離学習（特にTriplet）にGrad-CAMを適用して、可視化するのは難しい
• しかし、深層距離学習の場合、埋め込み空間上で近いものは似た特徴を持っているはず
• そこで、埋め込み空間上でデータベースを構築して近いものを参照することで、可視化が可能になるはず
• 実験の結果、Grad-CAM++（Triplet）に本手法を適用し、従来手法を上回る結果に
• さらに、通常、可視化能力はGrad-CAM"＜"Grad-CAM++だが、本手法を適用することでGrad-CAM"＝"Grad-CAM++くらいまで性能を引き上げることが可能に

Grad-CAMを適用する難しさ

※論文では、Tripletに主眼が置かれているため、ネットワークはTripletを使っているとします。

Grad-CAMを、Tripletの埋め込み空間上で適用した場合、論文では、二つの難しさがあるといっています。

• 埋め込み空間上では、全てのクラスのスコアが提供しているわけではない（そのため、クラス間の違いを見分ける根拠の可視化が難しい）
• テスト時に一枚の画像しか与えられないため（ペアではない）、Grad-CAMで使用する勾配を計算できない

#Grad-CAM
Grad-CAMのおさらいをしておきます。以下の文は、私の解釈も混じっているため、
正確な表現かは怪しいですが、ご容赦ください。

画像分類問題（犬 or 猫など）を考えます。

input画像が与えられたとして、Grad-CAMを適用したい層の出力をAとし、最終出力（例えば、犬のスコア）を
yとすると、以下のように偏微分することが可能です。

ただし、kはチャンネルの番号です。

これは、出力yは、各層の出力Aの関数と見なせるため、各層の出力で偏微分することが可能になって
います。そして、その偏微分した値が大きければ大きいほど、出力y（犬）と判断したことに大きく
寄与していると考えられます。

Grad-CAMでは、偏微分した値をそれぞれのチャンネルで平均化をして重みを計算しています。
当然、重みが大きければ大きいほど、重要度が高いチャンネルです。チャンネルkの重み$\alpha_k$は
以下で定義されます。

ただし、iとjは空間方向の広がりを表しています。ZはZ=i*jです。

##MobileNet V2を例に
（2）式と（3）式は直感的に分かりにくいです。
MobileNet V2を例にすると分かりやすいです。

MobileNet V2には、block_16_expand_reluという最終層に近い層の出力があります。
入力画像が96963（カラー）の場合、この層の出力は(33480)となります。

これは直感的にいうと、3*3サイズの特徴マップが480個あるということです。
画像を見分ける際、猫の場合、No.1-50の特徴マップが大きく寄与し、犬の場合、No.100-200の
特徴マップが大きく寄与しているケースなどが考えられます。従って、input画像に対し判断根拠の
可視化をするには、画像に対応した特徴マップの重みが必要になってきます。

このとき（3）式に当てはめると、k=480、i=j=3、Z=i*k=9となります。
チャンネルkの重み$\alpha_k$は480個存在しています。

Grad-CAMでは、この480個の出力に重みを付けて、大きく寄与したチャンネル（特徴）
ほど重要度が高いとして、可視化の際に重要視しています。（2）式、（3）式で計算した
重み$\alpha_k$に対し、出力$A_k$(3*3)を掛けて

\alpha_k\times A_k

が得られます。このときの出力は（3*3）です。大きく寄与した特徴マップほど大きな値に
なっています。そして、480個を一気に足して

\sum_k\alpha_k\times A_k

ヒートマップが得られます。ただし、このマップのサイズは33です。
最後に、この33を96*96にリサイズしてinput画像に合成しています。

※画像は「Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization」より引用

ただし、ヒートマップは0以下を切り捨てています。

#提案手法
本論文の焦点になるのは、

• この重み$\alpha_k$をデータベース化したい
• さらに、重要な（$\alpha_k$が大きい）チャンネルを絞った方がよいのでは？

ということです。順を追って説明します。

##重みのデータベース化
Tripletでも基本的に、Grad-CAMが適用可能です。これはペアで学習させたとしても
ペアの違いを見分けるように学習するため、クラスの違いを見分けるマップが作成される
ことが期待されるためです。

ここで、問題となるのは、ペアを使って可視化した場合、一部の特徴しか可視化
できないことが考えられます。この場合、あくまでもペア間の違いしか見分けない
ことが予想され、一部の特徴しか可視化されない可能性が考えられます。

そこで、論文では1つのペアだけではなく、複数のペアを用意し、それぞれの
マップを足せば、一部の特徴だけではなく、本質的な特徴の可視化が可能に
なるのではないかと考えています。

上の図はtripletを使って可視化した結果です。

• (a)：オリジナル画像
• (b)：1つのペアで可視化した場合
• (c)：50枚のペアで可視化した場合
• (d)：50枚のペアで、かつtop-50チャンネルで可視化した場合（提案手法）

ご覧のように複数のペアで可視化した方が、より本質的な可視化に成功している
ように見えます。

##重要なチャンネルを絞った方がよいのでは？
既に上の図で出てしましましたが、先行研究では、重要なチャンネルk（$\alpha_k$が大きい）だけを使って
Grad-CAMを適用すれば、より過不足なく可視化できることが報告されているらしいです。

MobileNetV2でいうと480チャンネル全てを使うわけではなく、$\alpha_k$が大きいtop-50の
チャンネルだけを用いて可視化するということになります。

##推論時の処理
Tripletを使っても、「複数のペアで可視化」と「top-50チャンネル」を使えば、過不足なく
可視化できることが分かりました。

では、推論時はどうするか？というと、データベースを作って参照する方式を
とっています。

まず、学習データを埋め込み空間上にプロットします。このとき似た特徴を持った画像は
近くにプロットされるため、「top-50のチャンネル」と「重み」は同じような番号、値に
なることが予想されます。

上の図は、データベース方式ではありませんが、テストデータをプロットし、
最近傍の学習データの「重み」をロードしてテストデータに適用した図です。
ご覧のとおり、どちらの画像も、赤い部分（似た特徴）が可視化されています。
ここで重要なのは、テストデータに対し一切計算（2,3式）をしていないという
ことです。つまり、近傍点のデータを参照することである程度可視化が成功します。

推論時は、最近傍ではなく、学習データのプロットをk-means（論文では、クラスタ数50）で
クラスタリングし、テストデータが属するクラスタ内で「重み」をロードしています。

ただし、事前に各クラスタの内部でGrad-CAMを適用し、チャンネルの重み$\alpha_k$の平均値と、
top-50チャンネル番号を保存しておく必要があります。

※正直言って、ここの処理は次回の記事の方が圧倒的に分かりやすいです。

##実験
論文では、「CUB200-2011」という鳥の画像データセットを使って実験しています。
このデータセットは鳥のマスク画像も用意されているため、可視化の定量的な評価が
可能になっています。

上の表はTripletを使って可視化した場合の、スコアを示しています。
Grad-CAMベースが左側、Grad-CAM++ベースが右側です。

青い線で囲まれた部分は、提案手法 with Grad-CAM++です。最も高いスコアを示しています。
ただ、Grad-CAM++ベースだと提案手法を用いても、さほどスコアはアップしていません。

次に、赤い線で囲まれた部分（Grad-CAMベース）だと、提案手法を用いることで大幅な
スコアの上昇が認められます。

さらに、普通の「Grad-CAM」を「++」レベルの能力まで引き出すことに成功しています。

上の図は、可視化した様子を表しています。

• (a)、(b)：オリジナル画像とマスク画像
• (c)：「Grad-CAM」を使って1つのペアで可視化した場合
• (d)：「Grad-CAM」を使って、50枚のペアで可視化した場合
• (e)：「Grad-CAM」を使って、50枚のペアで、かつtop-50チャンネルで可視化した場合（提案手法）
• (f)：「Grad-CAM++」を使って1つのペアで可視化した場合
• (g)：「Grad-CAM++」を使って、50枚のペアで可視化した場合
• (h)：「Grad-CAM++」を使って、50枚のペアで、かつtop-50チャンネルで可視化した場合（提案手法）

定量的な評価と同様に、提案手法をGrad-CAMに適用すると、一気に可視化が改善されます（e）。

論文では、家の価格を予想するタスクにも提案手法を適用しています。
気になる方は論文をご覧ください。

#個人的な感想

• そもそも、Tripletに普通のGrad-CAMが適用できるのが意外だった
• Grad-CAM++ベースだと、本手法の優位性があまりない（残念）
• 本手法の本当の凄さは、推論時にバックプロパケーション（偏微分）を不要にしたこと（応用すれば高速化が可能）

次回は、本手法を応用した「Faster-Grad-CAM」をご紹介します。
はっきりいって、爆速です。