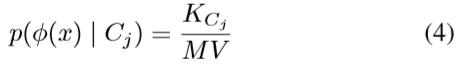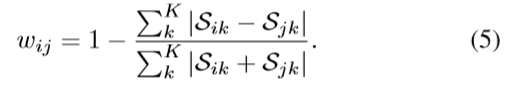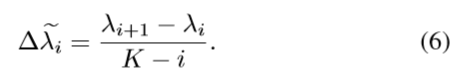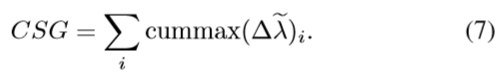畳み込みニューラルネットワーク(CNN)の学習には時間がかかります。
特に、転移学習を使わずに本気で精度を出そうとした場合、5日ほどかかる
時もあります。本稿で紹介する論文はデータセットの難しさを定量的に
評価することにより、CNNの学習を行わずに分類精度を高速に推定できる
というものです。
※コード全体はこちらに置きました。
※本稿の図は基本的に論文(Spectral Metric for Dataset Complexity Assessment)から引用しています。
※こちらの資料は【オンライン】pythonデータ分析勉強会#13 その2の発表資料です。
論文
概要
- CNNの分類問題で、CNNを学習させずにCNNの分類精度を推定できるCSGを提案
- 従来手法より高速化し(約2倍)、さらに相関係数を上昇させた(0.77→0.97)
クラスオーバーラップ
本論文のキーとなるのは、画像分類タスクにおいて「2つのクラス間の重複が大きければ
その分類問題は難しい問題」といえることです。
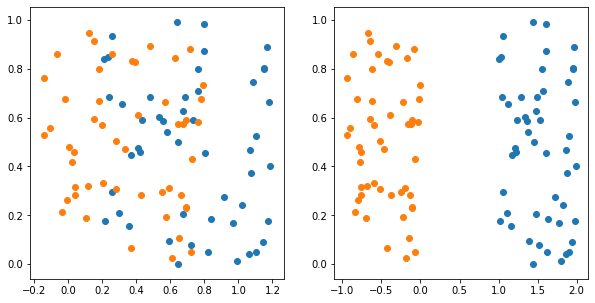
上の図は自作したものです。いま、CNNを使って画像を2次元空間を埋め込んだと
します。
そして、オレンジの点と青い点を分類するタスクだとして、左図に対し、
右図の方が分類しやすい問題といえそうです。これはいいかえると、
クラス間の重複が大きい方が難しい分類問題といえます。
数式で考えると、ある点の近傍で自分とは同じグループの点が多いと重複が
小さい(易しい分類問題)、自分と違うグループの点が多いと重複が大きい
(難しい分類問題)といえそうです。
論文では、以下の式を提示しています。
この式はクラス$C_i$から見たクラス$C_j$の重複度を表した式です。
MとVは一定値のため、ひとまず置いておいて、$K_{C_j}$はクラス$C_i$の画像xの
近傍にあるクラス$C_j$の個数です。つまり、$K_{C_j}$が大きいと重複が大きいと
いえます。
ここで、$\phi(x)\in R^d$は$C_i$の画像xを埋め込んだベクトル、Mは$C_j$から
抽出されたサンプル数、Vはハイパーキューブの大きさです。最終的に
クラス$C_i$の画像に(4)式を適用して和をとっています。
※はっきりいって、MもVも後で出てくる(5)式でキャンセルされるため、
M=V=1と置いても差し支えないかと思います。
(4)式はあくまでも2クラス間の重複度しか計算できないため、
複数のクラスがある場合は、各クラスの重複度をそれぞれ計算する
必要があります。
クラス数をKと置くと、類似行列(similarity matrix)$S\in R^{K\times K}$が
定義されます。$S_{ij}$は(4)式の和で計算されます。
$S$の各要素が大きいということは、(4)式が大きい値ということになり、
クラスiから見てクラスjが近くに多くあるということになります。
つまり、難しい分類問題と言えます。
スペクトラルクラスタリング
あとは、$S$を使って、どうやって分類問題の難しさを数値化するか
という問題です。
論文では、スペクトラルクラスタリングを使っています。
スペクトラルクラスタリングは元々、教師無し学習のクラスタリングで
使われる手法のようです。各グラフの結びつきが弱いところで分割
することで、k-means法などでは難しい分割問題でも、きれいに分割
することが可能です。詳しくは以下のリンクをご覧ください。
https://www.slideshare.net/pecorarista/ss-51761860
https://qiita.com/sakami/items/9b3d57d4be3ff1c70e1d
スペクトラルクラスタリングでは、以下のラプラシアンLの
固有値を求めることで、グラフの分割する難しさを数値化する
ことができます。
L=D-W
本論文に当てはめると、$S_{ij}$をグラフと見立て、分割の難しさ
(分類の難しさ)を数値化してくれます。一般的にはLの固有値が
大きいほど、分割が難しいとなるようですが、本論文では、後述するように
固有値の大きさだけではなく、固有値の傾向を捉えて数値化することで
より精度の高い数値化が可能になっています。
Lの式について、Dは$D_i=\sum_jw_{i,j}$と定義されます。
Wには$S$を直接代入したいところですが、Wには対称行列という制約が
あるため、以下の式を使って対称化しています。
実験結果を先に見せてしまうと、Wだけでもデータセットの難しさを
推定することができます。下の図はCIFAR10を使った実験結果です。
上段がWの実験結果。下段が学習させたAlexNetの推論による混同行列。
Wによる推定が、AlexNetの推論結果と酷似しているのが分かります。
「犬」と「猫」が判別しにくい状況も的中させています。
ラプラシアンL
ここまでの処理を確認しておきます。
画像 → 埋め込み → クラス間の重なりを(4)式で算出 → Lの固有値を計算
前述したようにラプラシアンLの固有値の最大値を見るだけで
グラフの分割の難しさ(本論文の場合、データセットの難しさ)を
推定することができます。
実験結果を先に見せてしまうと、固有値の最大値あるいは総和を
見るだけでも、データセットの難しさを推定することができます。
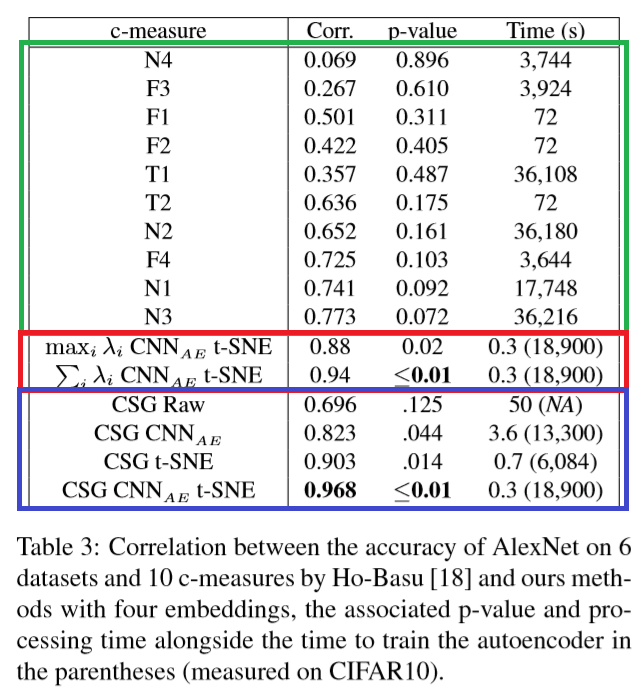
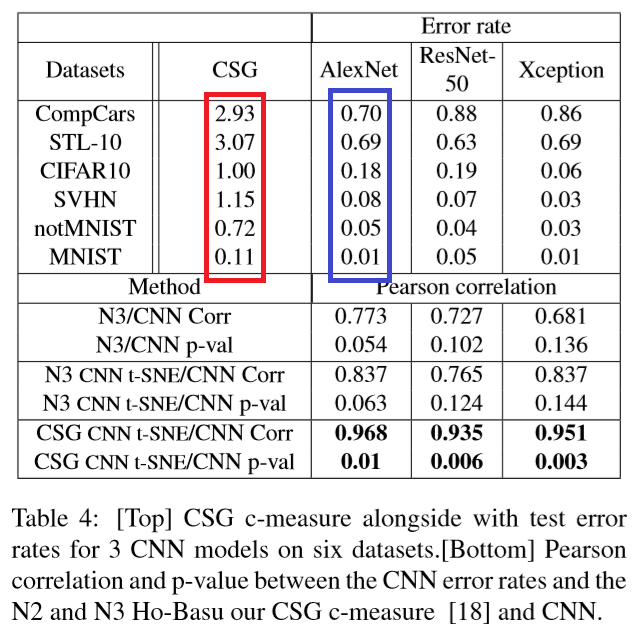
上の表はCIFAR10を使った実験結果。
- 緑の枠は従来手法。相関係数は高くても0.773。
- 赤の枠はLの固有値を使って算出した結果。固有値の最大値を使うと相関係数は0.88、総和だと0.94。
- 青の枠は後述するCSGを使った結果。相関係数は最も高い0.968。
固有値の総和を見るだけでも、従来手法を超える性能が出ます。
上の表では、「埋め込み手法」は以下の4つを用意しています。
- RAW:データそのまま。CIFAR10の場合1,024次元
- $CNN_{AE}$:オートエンコーダで獲得した潜在変数(次元数は不明)
- t-SNE:データをt-sneで次元圧縮。CIFAR10の場合1,024→2次元
- $CNN_{AE}$t-SNE:オートエンコーダによる潜在変数にt-SNEを適用
ちなみに、本論文の手法は「高速」を謳っていますが、オートエンコーダを学習させないと
良いCSGは算出できません。上の表で括弧書きになっている時間がオートエンコーダの学習時間です。
ご覧のとおり、従来手法に対し2倍速くなる程度です。(それでも凄いことですが。)
CSG
最後に、CSGについて説明します。
固有値を小さい方から順にi=0,1,2...と並べた場合、まずは次の式で標準化します。
そして、CSGを算出します。
ここで、cummaxとは[1,4,3,2]という配列があったとして、
cummax[1,4,3,2] = [1,4,4,4]
を意味します。つまり左から順に読み込んでいったときに、読み込んだ
数字の最大値を記録する関数です。
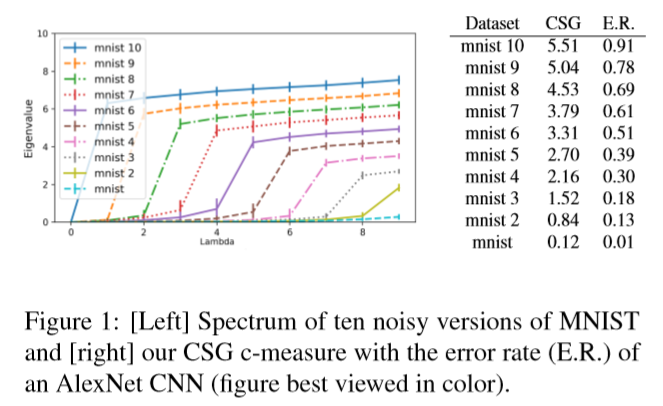
実験結果
ご覧のように、mnistに含まれるクラス数が増加するにつれ、CSGもエラー率も上がっていく
ことが分かります(相関関係)。ちなみに、水色のmnistは「mnist1」を意味しています。
すなわち、一つのクラスしかない状態です。
下の表は異なるデータセット(クラス数:10)を使った実験結果です。
注目すべきは、CSG(赤色)とAlexNetのエラー率(青色)が相関関係にあることです。
データセットが異なっていても、CSGが正しく機能していることが分かります。
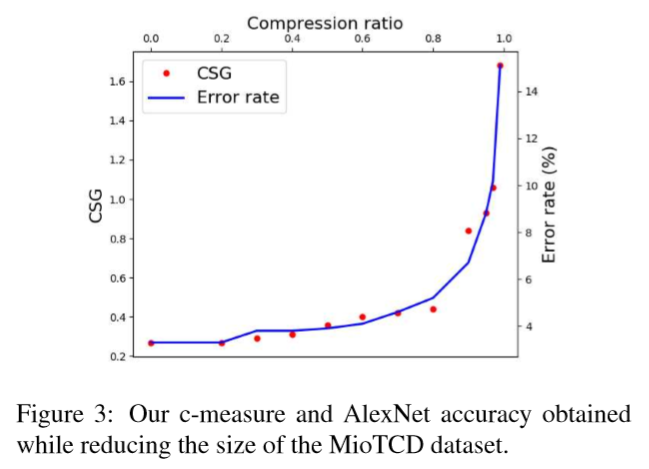
下の図は、MioTCDというデータセットを使った実験結果です。
ここでは、データ数を削減しながらCSGを計算しています。そして、CSGに
比例するようにエラー率も上がっていきます。このデータセットでは、
80%ほどのデータを削減しても問題ないことが分かります。
※この図では、一見CSGを使ったからエラー率が水平のまま推移していくように
見えますが、データ削減の方法は無作為に選んだものと思われます。
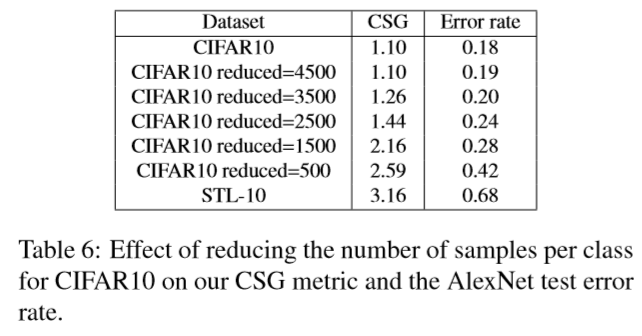
一方、CIFAR10では次の表にある通りデータを削減するにつれて
如実にエラー率が上がっていきます。
ここでもエラー率に比例してCSGが大きくなるのが分かります。
また、行列Wを使って、以下の式にMDSを適用することでクラス間の類似度を
可視化することができます。
S=1-W
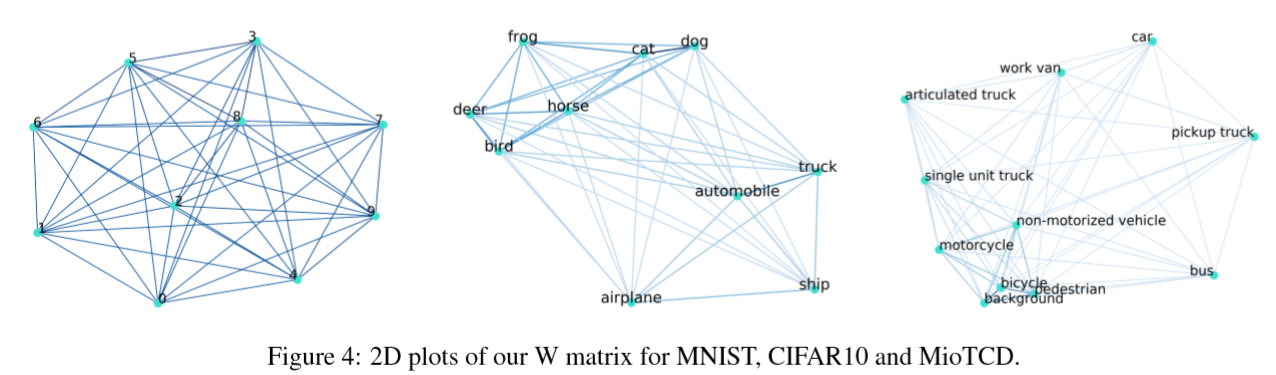
下の図はMDSを適用した図です。
MNISTはきれいにクラス間の距離が離れていますが、CIFAR10の場合、
「犬」と「猫」、「鹿」と「鳥」が近い位置にあり、似ていることが
分かります。つまり、これらは比較的判別が難しいということです。
実装
結論からいうと、MDSとWは何とか結果が出ましたが、肝心の
CSGはうまく再現しませんでした。
※コード全体はこちらに置きました。
実装条件
実験目的は「CIFAR10のデータを削減しながら、CSGの推移を見ます。」
つまり、Table6を再現します。
埋め込み用のオートエンコーダは以下の条件で実験しました。
- オートエンコーダは11層(論文では9層)
- 最適化手法はAdam(デフォルト)
- バッチサイズは128
- エポックは50を基本とし、データサイズによりエポックを変える(論文では100で固定)
埋め込み手法
埋め込み手法は論文で一番スコアが出た手法を採用します。
その手法とは、CSG $CNN_{AE}$ t-SNE です。
これは以下の手順で計算されます。
- 学習データでオートエンコーダ(エンコーダ+デコーダ)を学習させる
- エンコーダにテストデータを入れ、出力を取得する
- 出力をt-sneに入力し、埋め込みデータを得る
- 埋め込みデータでCSGを算出
苦心の安定化
実験で出したCSGはなかなか安定しません。そもそも、論文で出た固有値が
再現していないため、実装のどこかが間違えている気がするのですが、
私の実力では分かりませんでした。
何とか安定させるため、以下の対策を行っています。
-
テストデータの抽出
論文では、テストデータの抽出は各クラスから100個ずつとってこれば十分と
いっています。ところが、この100個に何が含まれるかでCSGがかなり変動します。
そのため、抽出は5回行ってCSGを計算し、平均値をとっています。 -
t-sne
t-sneはその都度、結果が異なるため、5回実行してCSGを計算し、平均値をとっています。
以上の対策の結果、各データサイズでCSGの計算は5×5=25回行い、平均値を算出しました。
実装結果
CSGは算出しましたが、相関係数が0.9くらいのときもあれば、0になることも
あるので、全く信用できないといえます。
ただし、WとMDSは論文と似たような結果になったので、報告します。
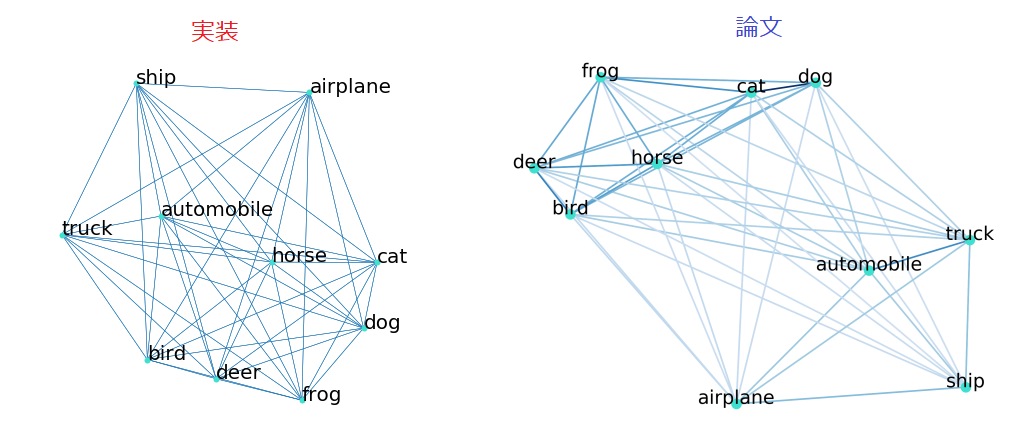
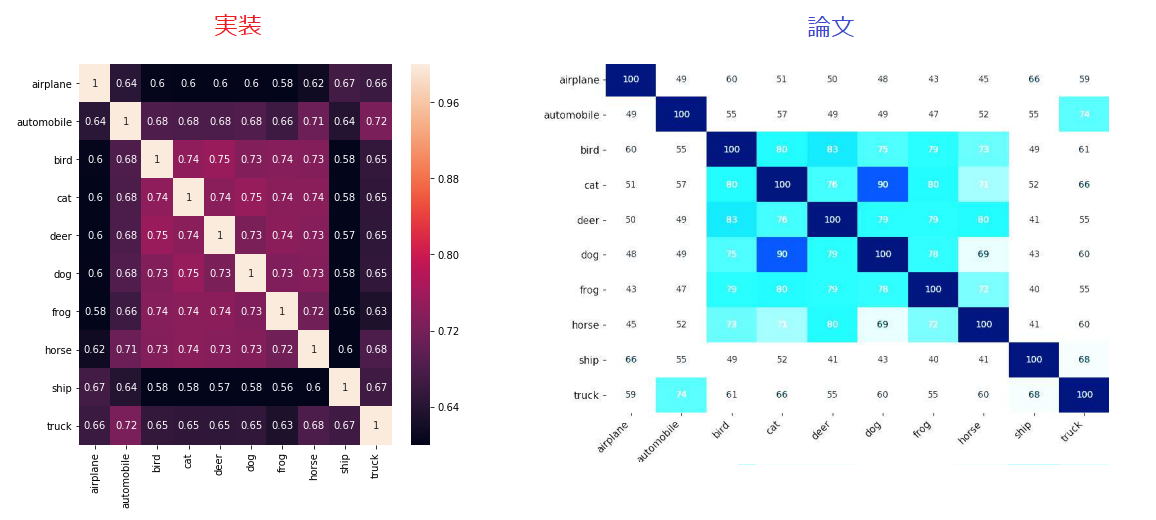
Wは似たような結果になったものの、「犬」と「猫」の類似度は論文のように
大きな値にはなりませんでした。
MDSの結果は、論文と似たようなものになりました。
ちゃんと、「cat」と「dog」、「deer」と「berd」が近い位置にきています。
実行速度
今回、ColaboratoryのGPUを使って検証しました。
GPUはまさかのTesla P100が出たため、一応括弧書きでTesla K80を使った時の
うろ覚えの時間も書いておきます。
- オートエンコーダの学習時間:3分30秒(30分)
- t-SNEの学習時間:7分(1時間)
上記の時間はCIFAR10のデータ全てを使った時の時間です。
ご覧のように、CNNを学習させて直接分類精度を見るより、実行速度が速いことが
分かります。
まとめ
- 実装により、CNNを学習させて直接分類精度を見るよりCSGを算出する方が速いことが分かりました。
- 実装でCSGは再現できませんでしたが、オートエンコーダ+t-SNEを適用することで、画像データの傾向を捉えることが可能です。
上記の知見を応用すると分類データ量の効率的な削減、データクレンジングで有効に
機能する可能性があります。それらの詳細は次回の記事で書きます。