スペクトラルクラスタリングについて解説します。
- スペクトラルクラスタリングとは
- 隣接行列
- グラフラプラシアン
- 固有値の意味
スペクトラルクラスタリングとは
グラフが与えられたときに、そのノードをクラスタに分類するアルゴリズムです。
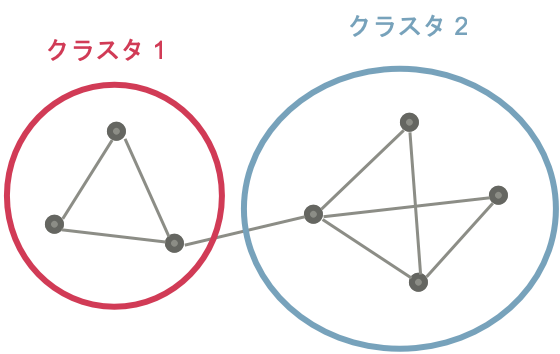
この説明では、
ノード ... グラフを構成する「点」
エッジ ... グラフを構成する「線」
を表します。
また、エッジが向きを持たない、無向グラフを対象とします。
スペクトラルクラスタリングでは、グラフラプラシアンと呼ばれる行列 $\mathcal{L}$ の固有値問題、
\mathcal{L}\boldsymbol{x} = \lambda \boldsymbol{x}
を解くことが最終目標になります。
ここで、$\boldsymbol{x}$ は各ノードに割り当てられた値を表します。
スペクトラルクラスタリングでは、各ノードに値を割り当てて、その値の大きさからクラスタを作成します。
つまり、最終的なアウトプットは、「各ノードに対応する値」 $\boldsymbol{x}$ になります。
ここから、適当なしきい値でグルーピングして、クラスタを作成します。
しきい値は、グループ内のメンバー数があまり偏らないほうがよいとか、グループ内の分散ができるだけ小さいほうがよい、など、必要に応じて基準を作って、それを最適化するようにしきい値を決める方法がいろいろ提案されています。
隣接行列
グラフを扱うにあたって、グラフを表現するのに便利な、隣接行列という概念を導入します。
隣接行列は、それぞれのノードがどのノードに対してエッジを張っているか、というのを行列の形で表現したものです。
隣接行列 $A$ では、$i$ 番のノードから $j$ 番のノードに張られたエッジの重みは、$A_{ij}$ になります。
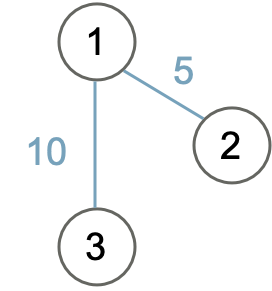
例えば図のようなグラフが与えられたときに、これを隣接行列で表現すると、
A =
\begin{pmatrix}
0 & 5 & 10 \\
5 & 0 & 0 \\
10 & 0 & 0
\end{pmatrix}
のようになります。
$A_{1, 2}$ には、1番のノードから2番のノードに張られたエッジの重みである、5が入っていることがわかります。

ここで、ノードの番号は適当に割り振ります。どの順に番号をつけても、結果は変わりません。
また、今回扱う無向グラフの場合、$i$ 番のノードから $j$ 番のノードに張られたエッジの重みと、$j$番のノードから $i$ 番のノードに張られたエッジの重みが等しいので、隣接行列は対称行列になります。
グラフラプラシアン
「各ノードに対応する値」 $\boldsymbol{x}$ を決めるために、最小化したい目的関数を以下のように設定します。
L(\boldsymbol{x}) = \frac{1}{2}\sum_{i, j} A_{ij} (x_i - x_j)^2
(目的関数 $L$ は、グラフラプラシアン $\mathcal{L}$ とは違うことに注意してください。)
ここで、$A$ は与えられたグラフの隣接行列、$x_i$ は「 $i$ 番目のノードに対応する値」を表します。
この目的関数を最小化することで、$x_i$ から $x_j$ に張られたエッジの重みが大きい(=結びつきが強い)ときは、$x_i$ と $x_j$ の値が近くなるように、それぞれのノードに対応する値を設定します。
もちろん、$\boldsymbol{x}$ の要素が全て同じ値の場合は、$L=0$ となって、最小の解が得られるのですが、ここではそれ以外の解を探します。
これから、目的関数を変形していきます。
まず、2乗の項を展開して、
\begin{align}
L(\boldsymbol{x}) &= \frac{1}{2}\sum_{i, j} A_{ij} (x_i - x_j)^2 \\
&= \frac{1}{2} \left(\sum_{i, j} A_{ij} (x_i^2 + x_j^2) - \sum_{i, j} A_{ij} 2x_ix_j \right)
\end{align}
隣接行列 $A$ は、無向グラフの場合は対称行列になるので、 $A_{ij} = A_{ji}$ より、
\sum_{i, j} A_{ij} x_i^2 = \sum_{i, j} A_{ij} x_j^2
です。
さらに、$\sum_{i, j} A_{ij} x_i^2$ で、$j$ に関して先に和を取ることができるので、
\sum_{j} A_{ij} = D_{ii}
と置くことによって、
\sum_{i, j} A_{ij} x_i^2 = \sum_i D_{ii} x_i^2
と書き直すことができます。
この $D$ を次数行列と言って、$A$ の $i$ 番目の列の要素の和が、$D$ の $i$ 番目の対角成分になります。

$D$ の対角成分以外の要素は0になります。
よって、
\begin{align}
L(\boldsymbol{x}) &= \frac{1}{2} \left(\sum_{i, j} A_{ij} (x_i^2 + x_j^2) - \sum_{i, j} A_{ij} 2x_ix_j \right) \\
&= \sum_{i, j} A_{ij} x_i^2 - \sum_{i, j} A_{ij} x_ix_j \\
&= \sum_{i} D_{ii} x_i^2 - \sum_{i, j} A_{ij} x_ix_j \\[3pt]
&= \boldsymbol{x}^{\mathrm{T}} D \boldsymbol{x} - \boldsymbol{x}^{\mathrm{T}} A \boldsymbol{x} \\[7pt]
&= \boldsymbol{x}^{\mathrm{T}} \mathcal{L} \boldsymbol{x} \tag{1}
\end{align}
ここで、
\mathcal{L} = D - A
と置いており、この $\mathcal{L}$ をグラフラプラシアンと呼びます。
さて、目的関数 $L$ を最小化するのですが、この値は $\boldsymbol{x}$ の長さを変えればどれだけでも小さくできてしまうため、
\boldsymbol{x}^{\mathrm{T}}\boldsymbol{x} = 1 \tag{2}
という制限を設けて、Lagrangeの未定乗数法を用いると、
\frac{\partial}{\partial \boldsymbol{x}} \left(\boldsymbol{x}^{\mathrm{T}} \mathcal{L} \boldsymbol{x} - \lambda(\boldsymbol{x}^{\mathrm{T}}\boldsymbol{x} - 1) \right) = 2\mathcal{L}\boldsymbol{x} - 2\lambda \boldsymbol{x}
となり、グラフラプラシアン $\mathcal{L}$ の固有値問題
\mathcal{L}\boldsymbol{x} = \lambda \boldsymbol{x} \tag{3}
を解けばよいことがわかります。
固有値の意味
さて、ここででてきた固有値 $\lambda$ の意味ですが、「目的関数の値」に対応します。
式 $(3)$ に、左から $\boldsymbol{x}^{\mathrm{T}}$ を掛けると、
\begin{align}
\boldsymbol{x}^{\mathrm{T}}\mathcal{L}\boldsymbol{x} &= \boldsymbol{x}^{\mathrm{T}}\lambda \boldsymbol{x} \\
&= \lambda\boldsymbol{x}^{\mathrm{T}}\boldsymbol{x} \\
&= \lambda
\end{align}
最後の変形には式 $(2)$ を使っています。
よって、式 $(1)$ を参照すると、
L(\boldsymbol{x}) = \lambda
となることがわかります。
つまり、スペクトラルクラスタリングでは、
\mathcal{L}\boldsymbol{x} = \lambda \boldsymbol{x}
を解き、小さい固有値 $\lambda$ に対応する $\boldsymbol{x}$ を選べば、それが目的関数 $L(\boldsymbol{x})$ を小さくするような解になっていることがわかります。
ここで、前述のように、$\boldsymbol{x}$ の要素が全て同じ値のときは$L(\boldsymbol{x})=0$ なので、 $\lambda = 0$ となります。
これ以外の解を求めたかったので、選びたい $\boldsymbol{x}$ は、0を除いた最小の $\lambda$ に対応する固有ベクトル、ということになります。