ディープラーニングで競馬予想

競馬に機械学習を使った試みはありますが、ディープラーニング（畳み込みニューラルネットワーク）を使った事例はあまり見かけません。

本稿では、畳み込みニューラルネットワーク（CNN）を使った競馬予想チャレンジをしてみます。

#競馬×機械学習
機械学習で競馬をガチで予想すると、70％くらいの的中率が出るようです。

こちらのリンクは大変参考になりますので、興味ある方はご覧ください。
https://exploratory.io/note/6412637879363595/2756560754330101/note_content/note.html

こちらの方は的中率80％くらいで、この前テレビにも出ていました。
https://logmi.jp/tech/articles/313650
https://www.youtube.com/watch?v=I1eSN6mPANs

#条件設定

今回競馬データを分析するに当たり、以下の条件を設定しました。

###1着の馬を当てる
単勝のみで勝負します。簡単で分かりやすいです。

###人気データは使わない
実際に運用することを考えると、当日の人気やオッズを調べる時間がない場合もあります。
常にパドックやPCの前に張り込んでいるわけにはいきませんので。

従って、レース前の人気は入力データとして使わないことにしました。

この場合、前日までに情報収集（スクレイピング）と機械学習で予想をして
余裕をもって馬券を購入することができます。

ただ、後述するように回収率を上げるためにはやはり、人気データは必須で
簡単な式を作ることで、人気データを使うことも検討してみました。

###血統データは使わない
血統データを入れるとデータが膨大になってしまうので、今回は割愛しました。

ただ、以前に血統データのみを使って機械学習で予想してみたことがあり、結構
良いところまで予想できたので、これを入れると的中率は上がると思われます。

###騎手データは使わない
血統データと同様に、騎手データも入れるとデータが膨大になってしまうので、今回は割愛しました。

###対象レースは東京の春のレース（未勝利及び500万以下）
東京の春のレース（未勝利及び500万以下）は比較的当てやすいと聞きます。
そこで、今回はこの時期のレースに絞って予想します。

#データの準備
##情報収集
情報収集は、以下に記事を参考にスクレイピングで集めました。
https://qiita.com/ishizakiiii/items/3b894b6e987fdf87093e

集めたデータの内訳は以下のとおりです。

	データ数	用途
1998年～2017年	911	学習データ及びバリデーションデータ
2018年	65	回収率シミュレーション用

データの形式は以下のとおりです。

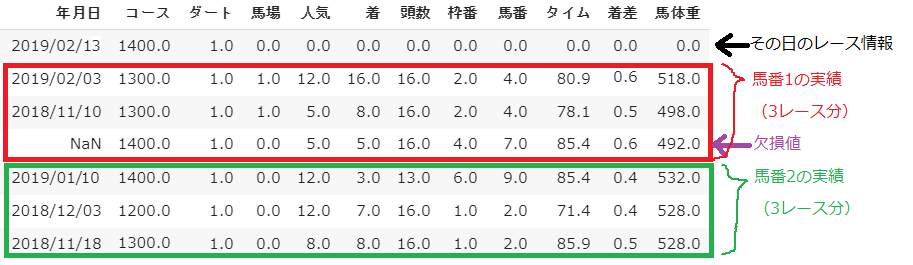
1行目にはその日のレース情報が入っています。ただし、「馬場」以降の列は0で埋めています。

2行目以降は各馬番の実績が入っています。上から1レース前、2レース前、3レース前と
なっています。そして、全部の行数は18頭分×3+「その日のレース情報」となっており、
全部で55行になっています。

列数は年月日を除くと11列あります。
まとめると、一レースにつき$55\times11$のデータ形式となっています。

各列の情報は以下のとおりです。

• 年月日
  CNNに投げるときに消しています。

• ダート
  ダートであれば「1」、芝であれば「0」です。

• 馬場
  良であれば「0」、それ以外なら「1」です。

• タイム
  秒単位に変換しています。

• 欠損値の扱い
  実績がないレースは「各列」の平均値で埋めています。
  また、18頭に満たないレースも18頭になるように平均値で埋めています。

#データの前処理
CNNに入れる入力は0～1の間にあるとうまくいくため、各列の値は最小値0、最大値1に
なるように変換しています。

##特徴量エンジニアリング
今のところ、生データの特徴量は「605」となっています。
不要な特徴量を減らすと、精度が上がることが報告されており、
今回はBorutaというパッケージを使って特徴量を減らしてみました。

Borutaについては、以下のリンクを参照ください。
https://qiita.com/KROYO/items/5ecabf99254f19818d8e
https://aotamasaki.hatenablog.com/entry/2019/01/05/195813

前述したようにデータのサイズは$55\times11$となっています。
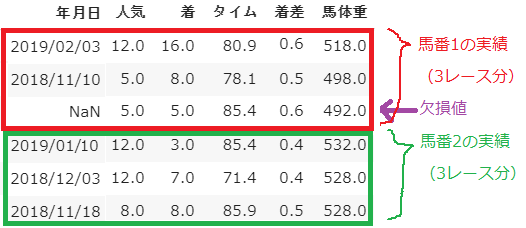
下の図はこのデータサイズに対し、Borutaで重要だと認められたものを色付けしたヒートマップです。

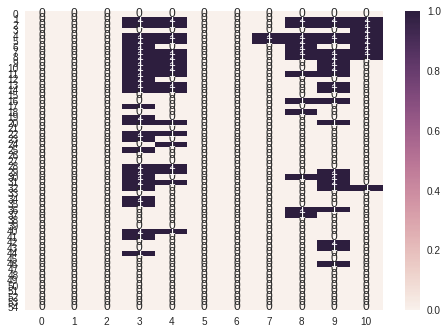
ヒートマップより「その日のレース情報」（1行目）は重要ではないということが分かりました。
そして、各列について「人気」「着」「タイム」「着差」「馬体重」が重要な要素といえそうです。

以上の検討から、最終的な入力データは以下の形式としました。

だいぶすっきりしました。当初、$55\times11$だったデータが$54\times5$まで圧縮できました。
本稿では、このデータを画像としてとらえてCNNで処理することにより一着になる馬を予想します。

一番意外だったのが「過去のレースの人気」が重要だということです。
過去のレースの人気は、潜在的な馬の能力（血統）を示唆しているのでしょうか。

ちなみに今回Borutaで特徴量を削減すると、精度が2％向上しました。
Boruta凄い！

#CNNで予想
ディープラーニングに興味のない方はここを読み飛ばして、回収率シミュレーションをご覧ください。

ここからはCNNを使っており、全て同一のものを使っています。
CNNのコードは付録に記載しています。

CNNの比較対象として、一番人気の馬券を買うことが挙げられるでしょうか。
一番人気の馬券は約30％の的中率が出ます。

##単純に予想してみる
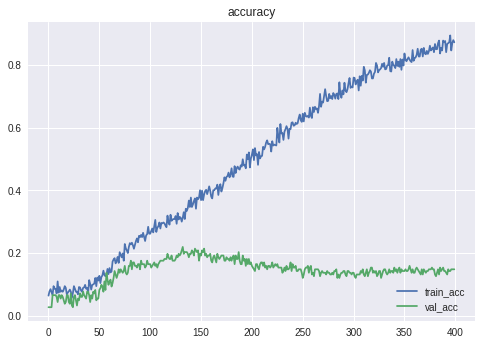
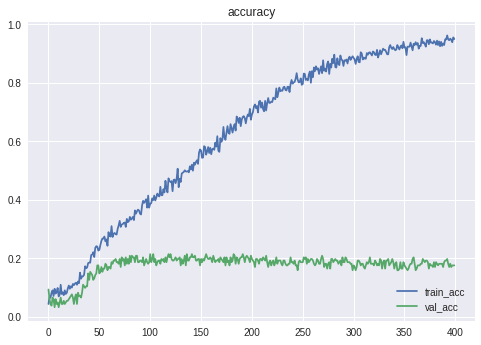
まずは、CNNで一着になる馬を予想してみます。

Epoch 133/400
729/729 [==============================] - 0s 335us/step - loss: 2.0631 - acc: 0.3128 - val_loss: 2.6475 - val_acc: 0.2198

Epoch 00133: val_acc improved from 0.20879 to 0.21978, saving model to weights.h5

精度は**21.98％**となりました。
残念ながら、一番人気の的中率には届きませんでした。

ちなみにXGBoostなどでも同程度の精度となりました。

CNNが過学習しているため、Ｌ２正則化などを盛り込んでみましたが、あまり効果はありませんでした。
また、CNNのフィルター（カーネル）サイズを横長や縦長に変えてみましたが、精度は悪化してしまいました。

##一番人気を予想してみる
単純に一着の馬を予想しても、一番人気の的中率に届きませんでした。

考え方を少し変えてみます。一番人気の的中率が高いのであれば、一番人気をCNNに
予想させてその馬券を買えば、的中率が上がるのではないでしょうか。

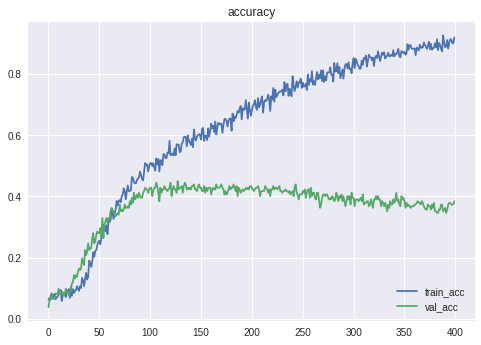
ということで、一番人気を予想してみます。

Epoch 00127: val_acc did not improve from 0.44505
Epoch 128/400
729/729 [==============================] - 0s 318us/step - loss: 1.3221 - acc: 0.5693 - val_loss: 1.8868 - val_acc: 0.4505

Epoch 00128: val_acc improved from 0.44505 to 0.45055, saving model to model/weights_pop.h5

「一番人気」の的中精度は45.06％となりました。

そして、一番人気だと予想した馬券を購入すると

test accuracy 0.24175824175824176

「一着」の的中精度は**24.18％**となりました。

単純に一着を予想するよりも、一番人気を予想させて馬券を購入した方が
的中率が高くなるとは...何とも不思議な現象です。

##割ってみる
今度はデータをいじってみます。
「人気」を「着」で割ると、人気通りであれば1に近くなり、人気から外れると
1より大きいあるいは、小さいものになります。何となく役立ちそうなデータです。

そこで、全ての列に対し総当たりで割り算を行いました。
ただし、データは0～1に変換しているため、分母に0.1を加算して演算します。

$X$を新たに作る特徴量、$x$を既存の特徴量とすると、以下の式になります。

X_{ij}=\frac{x_{ik}}{0.1+x_{il}}

ただし、$i$=1~54は行の番号、$j$は新たに作るデータの列の番号とします。
また、$k$と$l$($k\neq l$)には「人気」「着」「タイム」「着差」「馬体重」が入ります。

そして、割り算したデータ$(54\times10)$を元データ$(54\times5)$に連結し、
$(54\times15)$のデータとしてCNNで判定させます。

Epoch 104/400
729/729 [==============================] - 0s 351us/step - loss: 1.8688 - acc: 0.3992 - val_loss: 2.7059 - val_acc: 0.2143

Epoch 00104: val_acc improved from 0.21429 to 0.21429, saving model to model/weights_divide.h5

この時の精度は**21.43％**となりました。

単純に一着を予想させるのと、ほとんど変わらない精度になりました。

##掛けてみる
今度は掛け算を行ってみます。

さきほどと同じように、全ての列に対し総当たりで掛け算をしました。
$X$を新たに作る特徴量、$x$を既存の特徴量とすると、以下の式になります。

X_{ij}=x_{ik}x_{il}

ただし、$i$=1~54は行の番号、$j$は新たに作るデータの列の番号とします。
また、$k$と$l$($k\neq l$)には「人気」「着」「タイム」「着差」「馬体重」が入ります。

そして、掛け算したデータ$(54\times10)$を元データ$(54\times5)$に連結し、
$(54\times15)$のデータとしてCNNで判定させます。

Epoch 156/400
729/729 [==============================] - 0s 345us/step - loss: 1.3909 - acc: 0.5144 - val_loss: 2.8907 - val_acc: 0.2198

Epoch 00156: val_acc improved from 0.19780 to 0.21978, saving model to model/weights_times.h5

この時の精度は**21.98％**となりました。

##結果の比較

ここまでの結果をまとめておきます。

|通常予想|人気予想|除算（divide）|積（times）|一番人気|
|---|---|---|---|---|---|
|21.98％|24.18％|21.43％|21.98％|30％くらい|

残念ながら、CNNの予想は一番人気の的中率には届きませんでした。
次に、これらをアンサンブル学習してどこまで伸びるのか見てみます。

##ボツになった案
アンサンブル学習に行く前に、ボツになった案をご紹介します。

• DataAugmentation
  一着の馬のデータだけを他のレースデータとトレードしたり、ノイズを付与したり
  mixupしたりしてデータを水増ししましたが、精度は上がりませんでした。

• metric learning
  今回は学習データが1000以下と少なく、少ないデータ量でうまくいくと言われる
  metric learningを試しました。しかし、精度は上がりませんでした。

• 他の機械学習手法とアンサンブル
  XGBoostやCATBoost、ロジスティクス回帰やSVMとのアンサンブル学習を試みましたが、
  精度はほとんど変わりませんでした。

• 二段回学習
  CNNを特徴抽出器として利用し、抽出した特徴量をSVMやロジスティクス回帰で分類しましたが、
  精度は上がりませんでした。

#アンサンブル学習
もう少し悪あがきをしてみます。

運良く「一番人気」が分かったとして、CNNに何とか組み込めないか考えてみます。
そこで、一番人気とCNNでアンサンブル学習(Voting)してみます。

Votingについては、以下の記事をご覧ください。
https://qiita.com/shinmura0/items/bcc8c4a06b9a49c943d6#voting%E3%81%A8%E3%81%AF

式は独断で以下のとおりとしました。

Argmax(10\times popularity + CNN_{normal} + CNN_{times} + CNN_{divide} + CNN_{popularity})(1)

ただし、popularityは次式のようなone-hot表現になった18次元のベクトルです。

popularity = [0, 1, 0, ..., 0]

$CNN_{***}$は18頭の馬がそれぞれ一着になる確率が入った18次元のベクトルとなっています。

CNN_{***} = [0.1, 0.8, 0.1, ..., 0]

(1)式で最大のスコアになった馬を単勝予想馬とします。

お気づきのとおり、一番人気の係数が「10」になっており、一番人気を買うしか
選択肢はありません。従って、CNNの投票は全く関係ないようにみえますが
回収率を上げるときに大きな役割を果たします。

#馬券の買い方
回収率を上げる馬券の買い方について考察します。

##一番人気が既知の場合
(1)式の単勝予想馬について、その馬のスコアが高いとしたら信頼度は高いかもしれません。
スコアに閾値を設け、その値以上であれば、馬券を買う戦略をとってみます。

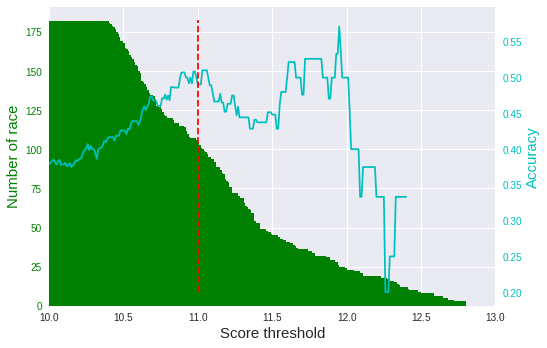
まずは、テストデータを使って、スコアの閾値と精度の関係を見てみます。

ご覧のとおり、スコアの閾値が高いほど精度も上がる傾向にあります。
ただ、閾値が高すぎると対象となるレース数が少なくなります（緑の棒グラフ）。

そこで、今回は閾値を「11」に定め（赤の点線）、ある程度レース数を確保することにしました。
テストデータだと50％くらいの精度が出ています。

##一番人気が未知の場合

一番人気が未知の場合、(1)式でpopularityの項がなくなります。
その場合も同じ戦略をとってみます。

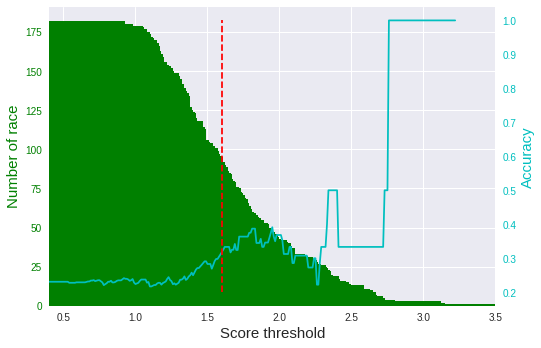
テストデータを使って、スコアの閾値と精度の関係を見てみます。

さきほどと同じく、レース数を確保するために閾値を「1.8」に定めました（赤の点線）。
テストデータだと30％くらいの精度が出ています。

#回収率シミュレーション

最後に2018年のデータを使って、回収率シミュレーションをしてみます。

##一番人気が既知の場合

ここでは（1）式がそのまま使えます。そして、閾値を「11」にして
スコアがそれ以上であれば、馬券を買う戦略をとります。

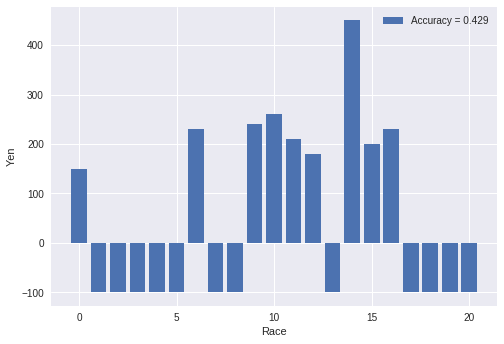
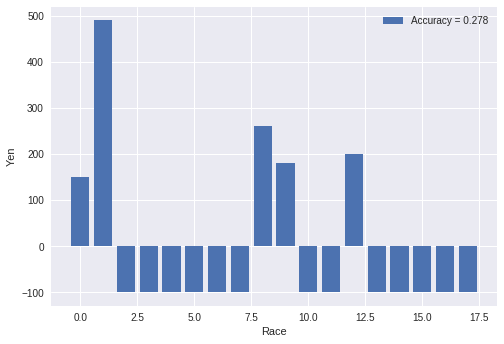
上の図は上記の戦略で単勝の馬券を買った場合の利益です。￥100で馬券を買ったとして、
当たれば「￥100×倍率」、負ければ「-￥100」としています。一番人気の馬券を
買っているため、的中しても倍率が非常に低いです。

	全レース	対象レース	的中	的中率	回収率
一番人気	65	65	20/65	30.8%	74.2%
アンサンブル学習	65	21	9/21	42.9%	102%

一番人気と比較した場合、アンサンブル学習の方が的中率も回収率も高いのですが、
回収率が102％なので、やる価値はあまりないです。
銀行に預金するより若干良いくらい！？

##一番人気が未知の場合

ここでは（1）式のpopularityがなくなっています。そして、閾値を「1.8」にして
スコアがそれ以上であれば、馬券を買う戦略をとります。

上の図は、上記の戦略で単勝の馬券を買った場合の利益を示しています。
2レース目の倍率は高いのですが、その他のレースは当たったとしても
一番人気っぽいので、利益が低くなっています。

	全レース	対象レース	的中	的中率	回収率
一番人気	65	65	20/65	30.8%	74.2%
アンサンブル学習	65	18	5/18	27.8%	71.0%

一番人気が未知の場合は回収率が100％を下回ってしまうので、買わない方が良いですね。
一番人気の情報は絶対必要です！

#まとめ

• ディープラーニングによる競馬データの予測は、**的中率43％、回収率102％**になりました。
• 今回のチャレンジでは、機械学習のモデルやハイパーパラメータをいじるより、特徴量をいじった方が精度が上がりやすかったです。やはり特徴量エンジニアリングが肝といえそうです。
• 1番人気のデータの重要性が良く分かりました。

#付録
最後にCNNのコードを示します。

import keras
from keras.models import Model
from keras.layers import Input, Dense, Activation, Dropout
from keras.layers import Conv2D, GlobalAveragePooling2D
from keras.layers import BatchNormalization, Add
from keras.callbacks import ModelCheckpoint
from keras.utils import to_categorical
from keras.initializers import he_normal
import keras.backend as K

# redefine target data into one hot vector
classes = 19
Y_train = to_categorical(y_train, classes)
Y_test = to_categorical(y_test, classes)

def cba(inputs, filters, kernel_size, strides):
    x = Conv2D(filters, kernel_size=kernel_size, strides=strides, padding='same', kernel_initializer=he_normal())(inputs)
    #x = BatchNormalization()(x) #バッチノーマライゼーションは入れない方が精度が出る
    x = Activation("relu")(x)
    return x

# define CNN
inputs = Input(shape=(X_train_.shape[1:]))

x = cba(inputs, filters=32, kernel_size=(3,3), strides=(2,2),)
x = Dropout(0.2)(x)
x = cba(x, filters=64, kernel_size=(3,3), strides=(2,2))
x = Dropout(0.2)(x)
x = cba(x, filters=128, kernel_size=(3,3), strides=(2,2))
x = Dropout(0.2)(x)

x = cba(x, filters=128, kernel_size=(3,3), strides=(2,2))
x = Dropout(0.2)(x)
x = cba(x, filters=256, kernel_size=(3,3), strides=(2,2))
x = Dropout(0.2)(x)
x = cba(x, filters=256, kernel_size=(3,3), strides=(2,2))
x = Dropout(0.2)(x)

x = GlobalAveragePooling2D()(x)
#x = keras.layers.Lambda(lambda xx: alpha*(xx)/K.sqrt(K.sum(xx**2)))(x) #metrics learning
x = Dense(classes)(x)
x = Activation("softmax")(x)

model = Model(inputs, x)
#model.summary()

# initiate Adam optimizer
opt = keras.optimizers.adam(lr=0.0001, decay=1e-6, amsgrad=True)

# Let's train the model using Adam with amsgrad
model.compile(loss='categorical_crossentropy',
              optimizer=opt,
              metrics=['accuracy'])

hist = model.fit(X_train_,Y_train,
                 validation_data=(X_test_,Y_test),
                 epochs=400,
                 callbacks=[ ModelCheckpoint(path + 'weights.h5', monitor='val_acc',
                                         verbose=1, mode='auto', save_best_only='true')],
                 verbose=1,
                 batch_size=50)

model_json = model.to_json()
open(path + 'model.json', 'w').write(model_json)

#結果描画
plt.figure()               
plt.title("loss")
plt.plot(hist.history['loss'],label="train_loss")
plt.plot(hist.history['val_loss'],label="val_loss")
plt.legend()
plt.show()

plt.figure()               
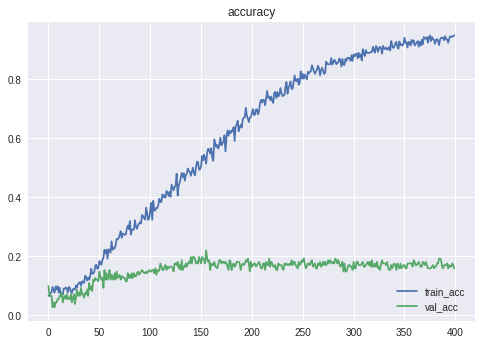
plt.title("accuracy")
plt.plot(hist.history['acc'],label="train_acc")
plt.plot(hist.history['val_acc'],label="val_acc")
plt.legend(loc="lower right")
plt.show()