カーネル主成分分析やSVM、ガウス過程で使われる「カーネル」は試行錯誤で
選定する必要があり、黒魔術的な要素を持っています。
今回ご紹介する論文は、ディープラーニングにカーネルの選定を任せてしまう
非常に意欲的な研究です。
※本稿の図は論文(Differentiable Compositional Kernel Learning for Gaussian Processes)より引用しています。
論文の概要
- ガウス過程で使われる「カーネルの選定」をディープラーニングに任せてしまう
- 全体は微分可能な形式となっており、勾配法で学習が可能
- 「回帰」、「ベイズ最適化」、「テクスチャーの補完」のタスクで良い成果を上げた
カーネルとは?
カーネルは、一般的に入力を非線形な空間へ飛ばし、そこでゴニョニョすることにより
線形分離不可能なデータであっても、うまく処理できる非常に便利なものです。
しかし、カーネルには種類があり、そして組み合わせも多くあり、どのように設計
すべきか非常に頭を悩ませます。
Neural Kernel Network
論文では、「ガウス過程」におけるカーネルの選定をディープラーニングに
任せてしまうことにより、最適な組み合わせを選ばせています。
これをNeural Kernel Network(NKN)と呼んでいます。
ガウス過程で使われるカーネルは、基本的に二つの入力に対し似ているもの
同士であれば小さい出力を、似ていないもの同士だと大きな出力を出します。
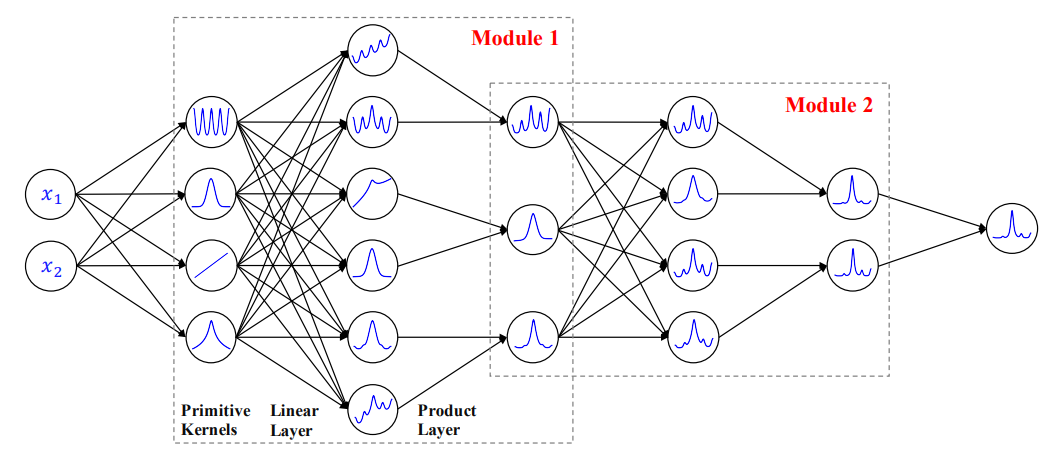
上の図は、ニューラルネットワークによるカーネル選定の様子を示しています。
$x_1$、$x_2$は入力を意味しています。二層目では多項式カーネルやガウスカーネルなど
を用意しておきます。三層目ではそれらに重みを付けて和をとります。四層目では
それらの積をとっています。ご覧のようにカーネル自体をニューラルネットワークに
埋め込んでいます。
そして、カーネルのパラメータもニューラルネットワークのパラメータとして
学習させています。
これにより人間はカーネルの設計や重みづけに悩まされることなく、ガウス過程を
使うことができます。要は楽になります。
実験結果
- 回帰
まずは、回帰の結果です。
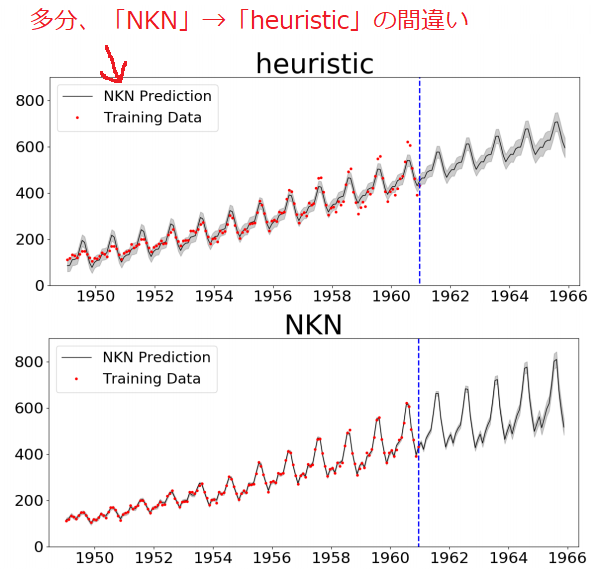
上の図は航空機の利用客数の推移をガウス過程で学習させたものです。
赤い点は学習データ、予測値は黒い線、グレーの領域は$1\sigma$です。
ご覧のように、ヒューリスティックな手法よりNKNの方が良くフィッティング
しています。1961年以降、実測値はありませんが、恐らくNKNの方が誤差が
小さいと思われます。
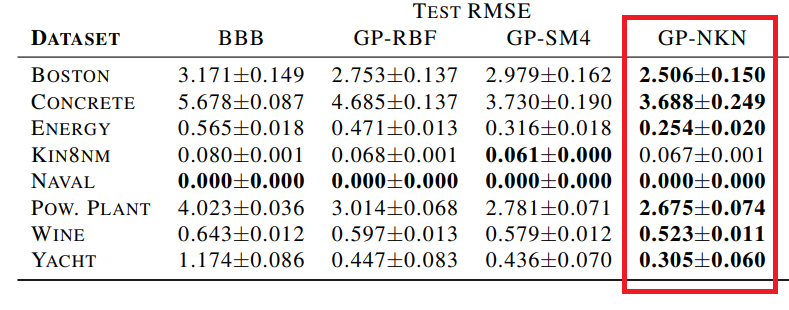
上の表は、種類の違う回帰のデータセットに対し、テストデータのRMSEを
計算したものです。他の手法に比べ、NKNの方がRMSEが小さくなっており、
より高精度に予測できているのが分かります。
- ベイズ最適化
次にベイズ最適化です。ベイズ最適化はよく油田の探索に使われています。
油田を探索するために穴を掘る必要がありますが、1つの穴を掘るのに莫大な
コストがかかるため、なるべく掘る回数を少なくしたいです。そのために、
堀った穴の状況から石油の分布を推測して、石油が一番多く埋蔵されている
場所を逐一予測する必要があります。そのときに使われるのがベイズ最適化です。
つまり、ベイズ最適化とは「できるだけ少ない試行回数で最適値を見つける」
タスクです。
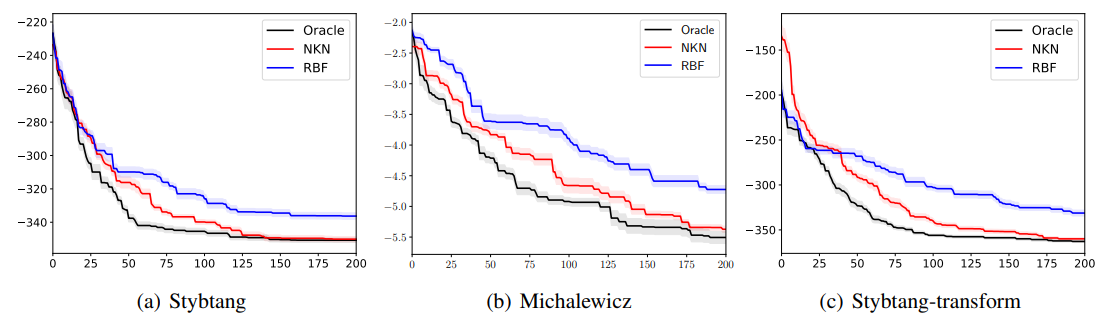
上の図は、異なるデータセット(a),(b),(c)でベイズ最適化を適用したものです。
横軸は試行回数、縦軸は評価関数の値です。評価関数の値をできるだけ小さくする
タスクだと思われます。
NKNは、Oracleには劣るものの、一般的に使われるRBF(ガウスカーネル)より
少ない試行回数で小さい値を見つけ出しています。
- テクスチャーの補完
最後にテクスチャーの補完です。
上の図で一番左(a)は学習データを意味し、真ん中がマスクされた図となっています。
(b)の図は正解を表しています。
ご覧のとおり、NKNが一番うまく再現できています。
個人的には、これが一番の驚きでした。
上の図も意味は同じです。
RBFだと歯が立たなかったものが、NKNだとうまく再現できています。
実装
著者によるTensorFlowの実装が公開されています。
感想
- NKNはカーネルの設計をお任せできるが、基礎となるカーネルは設計者の手で選ばなければならない。
- 回帰やベイズ最適化で良い性能を示しており、カーネル選定で迷ったらNKNという使い方もアリだと思われる。
- テクスチャーの補完はかなり高精度で、非CNN(畳み込みニューラルネットワーク)ベースを考慮すると、かなりの成果だと思われる。
実はテクスチャーの補完はある応用が可能で、私の方でコードを改造して
既に良い成果も出ています。その報告は次回させていただきます。