今回、ご紹介する論文は「モデル予測制御 X ガウス過程 X 自動運転」の
事例です。まずは、以下の動画をご覧ください。
Gaussian process MPC.... :Learning-based Model Predictive Control for Autonomous Racing https://t.co/K0h9wTA4Xo @YouTubeより
— Atsushi Sakai (@Atsushi_twi) July 12, 2019
とてもうまく自動運転できています。
この研究では、ガウス過程が使われており、「ガウス過程は、試行回数が
少ないという意味で強化学習より使えそう」などと考えてしまいましたが、
全く違う分野の研究でした。
結論としては、「サーキットなどの閉じられた環境であれば、強化学習より
使えるかも?」というレベルのお話しでした。
※本稿の図は論文(Learning-based Model Predictive Control for Autonomous Racing)から引用しています。
概要
- モデル予測制御を使った自動運転は、レースカーに軌道などの目標値を与えてそれに追従させる研究(モデル予測制御は、こちらを参考にしてください。とても分かりやすい解説です。)
- しかし、モデル(制御対象の運動方程式)に「誤差」があると、性能が落ちる
- 「モデルの誤差」をガウス過程で逐一推定することで、常にモデル誤差を更新し、精度良く制御することができる
恐らく、「エンジンの調子」や「タイヤの摩耗状態」など刻一刻と変わるモデル誤差を推定できていると思われます。
理論
論文では数式が山のように出てきますが、肝となるのは以下の式です。
x_{k+1}=f(x_k,u_k)+B_d(d(z_k)+w_k)
- x:状態量(レースカーの位置や角度など)
- u:入力
- $B_d$:
ムーアーペンローズの疑似逆行列 - d:モデル誤差
- w:ノイズ
上の式は、時刻kにおける状態($x_k$)や入力($u_k$)などが分かれば
時刻k+1の状態量($x_{k+1}$)が推定できるというものです。
式を変形します。
x_{k+1}-f(x_k,u_k)=B_d(d(z_k)+w_k)
上の式より、実際に時刻k+1の状態量($x_{k+1}$)を得たとして、推定値との差をとる
ことで、モデル誤差に関わる値d+wを取得することができます。ただ、この
モデル誤差は一定ではなく、レースカーの速度や角度によって変動します。
論文では、このd+wをガウス過程で推定しています。
なお、レースカーは自分の位置や角度などを各種センサーから取得しています。
結果
- トラック上の速度
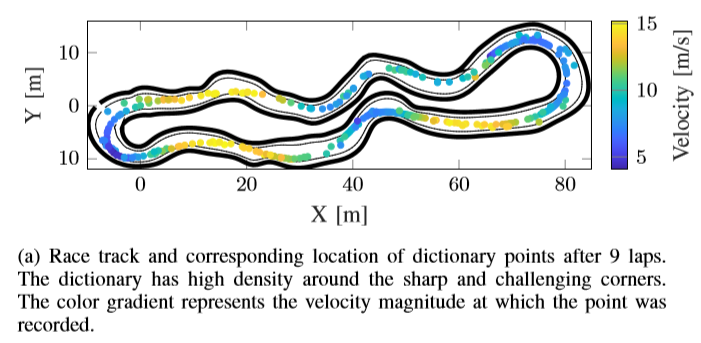
上の図は、トラック上のレースカーの速度を表しています。
黄色が強いほど速度が出ており、直線部で速度が出ていることが分かります。
- モデル誤差
上の図はモデル誤差を表しています。黒い点は実際のモデル誤差、青い線は
ガウス過程で推定したモデル誤差です。モデル誤差を高精度に推定できて
います。
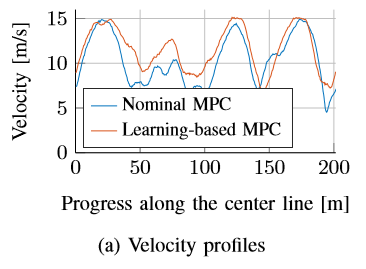
- 通常のモデル予測制御との比較
上の図はガウス過程を使った場合と、使わない場合(通常のモデル予測制御)との比較です。
横軸はスタートラインからの距離、縦軸は速度です。ガウス過程を使う(赤い線)と
速度の向上が認められます。
感想
- 少ない試行から回帰式を構築できる「ガウス過程」を応用したうまい研究
- 個人的には、リアルタイムでガウス過程を活用する発想はなかったので、目からウロコだった
- ロボットやドローンの制御に応用できそう(例えば、ドローンの重さや風の強さが変わっても、精度良く制御できる)
- あくまでも、モデル誤差を推定して性能を向上させる研究なので、PID制御やモデル予測制御で「ある程度」うまくいって事例であれば、適用しても効果は少ないと思われる。