不均衡データの取り扱い：Python機械学習の説明がさらっとしていたので、ちょっと深掘りした

はじめに

クラスごとの件数割合に大きな違いがある不均衡データを扱う機会が、私は割としょっちゅうあります。正常データはたくさんあるが、異常データは少ししかない状況はよくあります。
今までは実務で同僚のコードなどで対処法を身に付けたのですが、python機械学習6章最後に記載してある不均衡データの扱いに関する説明を読んでみることにしました。
この本では、データの処理については書いてありますが、それぞれの手法でモデルを作ったらどうなるか、などは一切書いてありません。そこで、自分なりに補いながら手を動かしたことをこの記事に纏めます。

Python機械学習の本にならって、データとしては良性腫瘍と悪性腫瘍に関するthe Breast Cancer Wisconsin datasetを使います。モデルとしては、ロジスティック回帰を使ってこの２つを分類することにします。

腫瘍の判別においては、悪性腫瘍を見逃してしまうことを避けたいです。ですから、評価指標としてはrecallを使います。accuracyやprecisionはこの記事では評価対象としません。

準備

まず、必要なライブラリをインポートしておきます。

import pandas as pd
import numpy as np

from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import make_pipeline

from sklearn.model_selection import train_test_split

import matplotlib.pyplot as plt
plt.style.use('ggplot')

from sklearn.model_selection import StratifiedKFold, cross_val_score

from sklearn.metrics import confusion_matrix
from sklearn.metrics import recall_score

データとして、この本の６章で一貫して使われているthe Breast Cancer Wisconsin datasetを読み込みます。
このデータのダウンロードは私には少し分かりずらかったのですが、このページの「wdbc.data」をクリックしてダウンロードします。

df = pd.read_csv('./rawdata/wdbc.data', header=None)
df.iloc[:,1].value_counts()

B 357
M 212
Name: 1, dtype: int64
benign tumors （良性腫瘍）が357件、malignant tumors （悪性腫瘍）が212件あるデータセットとなっています。
以下のコードで、通常の様に説明変数のXと目的変数yを作り、LabelEncoderを使って目的変数を0,1に数値化します。

#説明変数
X = df.loc[:,2:].values
#目的変数
y = df.loc[:,1]

# 目的変数を0,1に数値化
from sklearn.preprocessing import LabelEncoder

le = LabelEncoder()
y=le.fit_transform(y)

ここで、不均衡データを作ります。悪性腫瘍のデータを40件にまで減らし、357:40の不均衡データにします。この不均衡データを訓練データとテストデータに分割します。（ここから、本とはデータの扱いが変わっています。本ではデータ分割はせずにUpsamplingなどを行うだけで、モデルは作っていません）

X_imb = np.vstack( (X[y==0], X[y==1][:40]) )
y_imb = np.hstack( (y[y==0], y[y==1][:40]) )

X_imb_train, X_imb_test, y_imb_train, y_imb_test = train_test_split(X_imb, y_imb, test_size=0.30, stratify=y_imb, random_state=1)

print('# train 0 : ', len(y_imb_train[y_imb_train==0]))
print('# train 1', len(y_imb_train[y_imb_train==1]))

print('# test 0', len(y_imb_test[y_imb_test==0]))
print('# test 1', len(y_imb_test[y_imb_test==1]))

　#train 0 : 249
　#train 1 28
　#test 0 108
　#test 1 12
悪性腫瘍データ40件を28:12に分割しています。良性腫瘍データも同じ比率になるようにしています。
これで準備が完了しました。

class_weightをつかう

損失関数を評価するときに、データ数が少ない悪性腫瘍クラスのデータに重みを付けて、両クラスのバランスをとろうとする方法です。
scikit learnのLogisticRegressionでは引数として class_weight='balanced' を指定します。
比較するため、class_weight=Noneを指定し、ウェイトをつけず悪性腫瘍は損失関数に少ししか寄与しない場合も確認します。
make_pipelineを使って、説明変数の標準化とロジスティック回帰モデル作成のパイプラインを作っておきます。

pipe_lrbl = make_pipeline( StandardScaler(),
                       LogisticRegression(penalty='l2',random_state=1,class_weight='balanced') )

pipe_lrno = make_pipeline( StandardScaler(),
                       LogisticRegression(penalty='l2',random_state=1,class_weight=None) )

cross_val_scoreで評価

はじめにtrainデータを使って、交差検証（クロスバリデーション）でclass_weightを付けた時、付けないときの精度の平均とばらつきを確認します。
交差検証では、データを10個に分割して実施することにします。

skfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)

はじめにclass_weight='balanced'を指定したほうで実施します。

recall_lrbl = cross_val_score(estimator=pipe_lrbl, X=X_imb_train, y=y_imb_train, scoring='recall', cv=skfold, verbose=0)
print( np.mean(recall_lrbl) )
print( np.std(recall_lrbl) )

平均(mean) 0.9333333333333332
標準偏差(std) 0.13333333333333336

次にclass_weight=Noneのときの結果です。

recall_lrno = cross_val_score(estimator=pipe_lrno, X=X_imb_train, y=y_imb_train, scoring='recall', cv=skfold, verbose=0)
print( np.mean(recall_lrno) )
print( np.std(recall_lrno) )

平均(mean) 0.9
標準偏差(std) 0.13333333333333336

class_weight='balanced'としたほうが、recallの平均値が高く、バラつきは小さくなっており、少しばかりですが良い結果となっています。不均衡データを考慮した効果が表れています。

testデータを使って検証

trainデータを全部使ってモデルを作成し、testデータに対するrecallを評価することで、class_weightに'balanced'とNoneを設定した時の差を確認します。
まず、class_weight = 'balanced'としたときです。

# class_weight = 'balanced'のとき
model_lrbl = pipe_lrbl.fit(X_imb_train, y_imb_train)
y_pred_lrbl = model_lrbl.predict(X_imb_test)
print( confusion_matrix(y_true=y_imb_test, y_pred=y_pred_lrbl) )
print( recall_score(y_true=y_imb_test, y_pred=y_pred_lrbl) )

混同行列
[[108 0]
[ 2 10]]
Recall : 0.8333333333333334

# class_weight = Noneのとき
model_lrno = pipe_lrno.fit(X_imb_train, y_imb_train)
y_pred_lrno = model_lrno.predict(X_imb_test)
print( confusion_matrix(y_true=y_imb_test, y_pred=y_pred_lrno) )
print( recall_score(y_true=y_imb_test, y_pred=y_pred_lrno) )

混同行列
[[108 0]
[ 3 9]]
Recall : 0.75

class_weight='balance'としたほうが、完全なアウトサンプルであるテストデータに対するrecallが良くなっています。不均衡データを考慮した効果がここでは出ていますね。

resampleを使ってUpsampling

次に、単純にデータ数が少ない悪性腫瘍データをサンプリングで増やすアップサンプリングを実施します。全く同じ内容のデータを複製してデータ件数を水増しするので、過学習が起こる懸念はありますが、やってみます。

from sklearn.utils import resample
print('Number of class 1 sample before', X_imb_train[y_imb_train==1].shape[0])
X_upsampled_train, y_upsampled_train = resample(X_imb_train[y_imb_train==1], y_imb_train[y_imb_train==1],
                                               replace=True, n_samples=X_imb_train[y_imb_train==0].shape[0],
                                               random_state=123)
print('Number of class 1 sample after', X_upsampled_train[y_upsampled_train==1].shape[0])

Number of class 1 sample before 28
Number of class 1 sample after 249

X_bal_train = np.vstack( (X_imb_train[y_imb_train==0], X_upsampled_train) )
y_bal_train = np.hstack( (y_imb_train[y_imb_train==0], y_upsampled_train) )

print('number of 1 after upsampling', len(y_bal_train[y_bal_train==1]))
print('number of 0 after upsampling', len(y_bal_train[y_bal_train==0]))

number of 1 after upsampling 249
number of 0 after upsampling 249

アップサンプリングにより、両クラスとも249件ずつのデータとなっています。

cross_val_scoreで評価

アップサンプリングしたtrainデータに対してcross_val_scoreを使って評価してみます。

recall_lrup = cross_val_score(estimator=pipe_lrno, X=X_imb_train, y=y_imb_train, scoring='recall', cv=skfold, verbose=0)
print( np.mean(recall_lrup) )
print( np.std(recall_lrup) )

平均(mean) 0.9
標準偏差(std) 0.1527525231651947
この結果は、データが不均衡なままで、class_weight=Noneのときの結果と変わりませんでした。

testデータを使って検証

次に、アップサンプリングしたtrainデータをつかってモデルを作り、testデータでrecallを検証します。

model_lrup = pipe_lrno.fit(X_bal_train, y_bal_train)
y_pred_lrup = model_lrup.predict(X_imb_test)
print( confusion_matrix(y_true=y_imb_test, y_pred=y_pred_lrup) )
print( recall_score(y_true=y_imb_test, y_pred=y_pred_lrup) )

混同行列
[[108 0]
[ 2 10]]
recall 0.8333333333333334
testデータに対するrecallは、上のclass_weight='balanced'としたときと同じ値となり、一定の効果が確認されます。

SMOTE

Python機械学習の本には紹介してあるだけで、pythonを使ったやり方は書いていなかったので、自分で調べて簡単にやってみました。
SMOTEとはSynthetic Minority Oversampling TEchniqueの略です。　Synthetic（合成の、人工的な）とある通り、データを人工的に生成する手法です。件数がすくないクラスに対して、実際にあるデータ点を線で結び、線上の任意の点をランダムに選んでデータを増やす手法です。

pythonで実装するには、imblearnをインストールする必要があります。
私はanacondaを使っているので、以下のコマンドでインストールしました。

$ conda install -c conda-forge imbalanced-learn

この後で、以下の様にしてSMOTEによるオーバーサンプリングを実施します。

from imblearn.over_sampling import SMOTE
rat = y_imb_train[y_imb_train==0].shape[0]/ y_imb_train[y_imb_train==1].shape[0] 
smote = SMOTE( sampling_strategy={ 0:len(y_imb_train[y_imb_train==0]), 1:int( len(y_imb_train[y_imb_train==1])*rat ) } )
X_smote, y_smote = smote.fit_resample(X_imb_train, y_imb_train)

print('X_smote.shape', X_smote.shape)
print('# of 0 after SMOTE', len(y_smote[y_smote==0]))
print('# of 1 after SMOTE', len(y_smote[y_smote==1]))

X_smote.shape (498, 30)

of 0 after SMOTE 249

of 1 after SMOTE 249

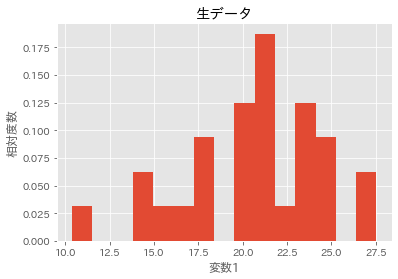
こちらでも良性腫瘍と悪性腫瘍の件数が同じに調整されました。データがどのように生成されているかを確認してみます。

# SMOTE前
plt.hist(X_imb_train[y_imb_train==1][:,1], bins=15, density=True)
plt.title('生データ')
plt.xlabel('変数1')
plt.ylabel('相対度数')

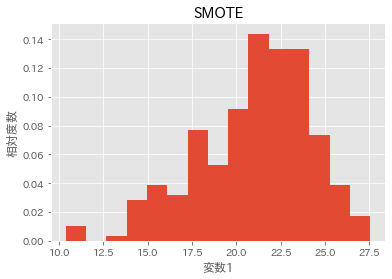
#SMOTE後
plt.hist(X_smote[y_smote==1][:,1], bins=15, density=True)
plt.title('SMOTE')
plt.xlabel('変数1')
plt.ylabel('相対度数')

SMOTE前の生データの分布

SMOTE後の生成されたデータの分布

データが補完されて生成されていることが分かります。

cross_val_scoreで評価

SMOTEしたtrainデータに対して、cross_val_scoreを使います。

recall_lrsm = cross_val_score(estimator=pipe_lrno, X=X_imb_train, y=y_imb_train, scoring='recall', cv=skfold, verbose=0)
print( np.mean(recall_lrsm) )
print( np.std(recall_lrsm) )

平均(mean) 0.9
標準偏差(std) 0.1527525231651947
この結果は、データが不均衡なままで、class_weight=Noneのときの結果と変わりませんでした。

testデータを使って検証

次に、SMOTEしたtrainデータをつかってモデルを作り、testデータでrecallを検証します。

model_lrsm = pipe_lrno.fit(X_bal_train, y_bal_train)
y_pred_lrsm = model_lrsm.predict(X_imb_test)
print( confusion_matrix(y_true=y_imb_test, y_pred=y_pred_lrsm) )
print( recall_score(y_true=y_imb_test, y_pred=y_pred_lrsm) )

混同行列
[[108 0]
[ 2 10]]
Recall 0.8333333333333334

testデータに対するrecallは、上のclass_weight='balanced'としたとき、及びアップさんブリングしたときと同じ値となります。今回は、単なるアップサンプリングではなく、SMOTEでデータを人工的に生成したことによる優位性は確認できませんでした。

まとめ

異常データが少ないなど、不均衡データを扱うことはそれなりにあります。
今回は自分の知識の整理のためPython機械学習を再度読んでみました。この本ではモデルを作るところまでは記載していなかったり、SMOTEは紹介してあるだけだったので、自分で補ってみました。
自分なりの補い方には、誤りや不完全な点があるかもしれませんので、ご指摘いただければと思います。
class_weigth、アップサンプリング、SMOTEで実際にcross_val_scoreを使った評価、testデータを使った評価を行いました。今回使ったデータでは、不均衡なデータのままでもそれなりのrecallのモデルを作れるので、これら３手法の優位性をはっきりとは確認できていないかもしれません。今後、不均衡データに出会った時に、またこれらの手法を試したいです。
あと、不均衡データに対しては、バギングを使う手法もあるのですが、こちらを今度はしっかり調べてみたいです。