この記事は、Kyoto University Advent Calendar 2020の14日目の記事です。
13日目の記事はlzpelさんの「ステイホームで乱れた生活習慣を機械学習を使って改善する話 #kuac2020」でした!電子工作できる方は本当に素直にかっこいいと思いますし、それを実生活にダイレクトに生かせるのも素晴らしいと思います!ぜひ読んでください!!
1. 自己紹介
工学部物理工学科材料科学コース2回生の伊勢志摩と申します。お笑いと格闘技とプロレスと秋元系アイドルを心から愛してます。今も青春高校3年C組アイドル部の曲を聞きながらこの記事を書いています。この記事も(広義)自分の趣味の布教です。みんなM-1見てください。敗者復活からちゃんと見てください!
最近競プロやkaggleにハマったのですが、なかなか同じ趣味の方とつながれてません... ぜひ同じ趣味の方お話してください!もちろん自分からも積極的に行こうと思います!
9日目の記事で少し言及していただいたのですが、京大の学習支援サイトであるPandAに追加された課題をGoogleカレンダーに追加するツール(もどき)を制作したことがあります。
2. この記事について
来る12月20日にM-1グランプリ2020の決勝があります。いちお笑いファンとしてただただ楽しみで仕方ありません。ところで、今回の審査員は2018年,2019年と同じ顔ぶれです。そこでこの記事では、主成分分析と呼ばれる手法を用いて前年と前々年の決勝のデータを分析することで、この審査員下のM-1では何が評価されているのか分析したいと考えています。
3. 扱うデータ
この章では2018,2019年のM-1の採点結果を敬称略でご紹介します。以下ではこのデータを分析していきます。
3.1. 2018年度の採点結果
| コンビ名 | 巨人 | 礼二 | 塙 | 志らく | 富澤 | 松本 | 上沼 | 順位 |
|---|---|---|---|---|---|---|---|---|
| 霜降り明星 | 93 | 96 | 98 | 93 | 91 | 94 | 97 | 1 |
| 和牛 | 92 | 94 | 94 | 93 | 92 | 93 | 98 | 2 |
| ジャルジャル | 93 | 93 | 93 | 99 | 90 | 92 | 88 | 3 |
| ミキ | 90 | 93 | 90 | 89 | 90 | 88 | 98 | 4 |
| かまいたち | 89 | 92 | 92 | 88 | 91 | 90 | 94 | 5 |
| トム・ブラウン | 87 | 90 | 93 | 97 | 89 | 91 | 86 | 6 |
| スーパーマラドーナ | 87 | 90 | 89 | 88 | 89 | 85 | 89 | 7 |
| ギャロップ | 87 | 90 | 89 | 86 | 87 | 86 | 89 | 8 |
| 見取り図 | 88 | 91 | 85 | 85 | 86 | 83 | 88 | 9 |
| ゆにばーす | 84 | 91 | 82 | 87 | 86 | 80 | 84 | 10 |
3.2. 2019年度の採点結果
| コンビ名 | 巨人 | 礼二 | 塙 | 志らく | 富澤 | 松本 | 上沼 | 順位 |
|---|---|---|---|---|---|---|---|---|
| ミルクボーイ | 97 | 96 | 99 | 97 | 97 | 97 | 98 | 1 |
| かまいたち | 93 | 94 | 95 | 95 | 93 | 95 | 95 | 2 |
| ぺこぱ | 93 | 92 | 94 | 91 | 94 | 94 | 96 | 3 |
| 和牛 | 92 | 93 | 96 | 96 | 91 | 92 | 92 | 4 |
| 見取り図 | 94 | 93 | 92 | 94 | 91 | 91 | 94 | 5 |
| からし蓮根 | 93 | 93 | 90 | 89 | 90 | 90 | 94 | 6 |
| オズワルド | 91 | 94 | 89 | 89 | 91 | 90 | 94 | 7 |
| すゑひろがりず | 92 | 91 | 91 | 92 | 90 | 89 | 92 | 8 |
| インディアンス | 92 | 92 | 89 | 87 | 90 | 88 | 94 | 9 |
| ニューヨーク | 87 | 88 | 91 | 90 | 88 | 82 | 90 | 10 |
4. 実装パート
この章では主成分分析を用いて上記のデータを分析するコードの実装とその結果表示されるグラフを記載します。意見が分かれるところとは思いますが、今回は2つのデータを結合して分析します。また、主成分分析の詳しい説明はここでは記載しません。審査員の出した点数から、「審査員が重要視した2つの成分」を抽出する手法であるという説明にとどめます。
上位3組、つまりファイナルラウンドに進出できたコンビは青色、それ以外は赤色でプロットされるよう実装しました。またこの際、この記事を大変参考にさせていただきました。ありがとうございます。実装コードは以下のようになります。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn.preprocessing import scale
from sklearn.decomposition import PCA
df_2018 = pd.read_csv('./M1_2018_.csv')
df_2019 = pd.read_csv('./M1_2019_.csv')
df_2018.columns = ['コンビ名','巨人','礼二','塙','志らく','富澤','松本','上沼','順位']
df_2019.columns = ['コンビ名','巨人','礼二','塙','志らく','富澤','松本','上沼','順位']
judge = ['巨人','礼二','塙','志らく','富澤','松本','上沼']
col = ['コンビ名','巨人','礼二','塙','志らく','富澤','松本','上沼','順位']
df = pd.merge(df_2018,df_2019,on=col,how='outer')
x = np.array(df[judge].values) #データを得る
t = np.array([int(i) for i in df["順位"].values])
x_scaled = scale(x)
x_pca = PCA(n_components=2).fit_transform(x_scaled)
plt.figure(figsize=[10,4])
plt.subplot(1,2,1)
for i in range(len(t)):
plt.plot(x_pca[i,0],x_pca[i,1],c= 'b' if t[i]<=3 else 'r',marker='o',alpha=0.7)
plt.annotate("{}\n{}点".format(df.iloc[i,0][:3], sum(df.iloc[i,1:-1])),x_pca[i]+[.1,0])
plt.xlim([min(x_pca[:,0])-.5, max(x_pca[:,0])+.8])
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.subplot(1,2,2)
comps = PCA(n_components=2).fit(x_scaled).components_
for i in range(len(judge)):
plt.plot([0,comps[0,i]],[0,comps[1,i]],c=cm.Greens(np.linalg.norm(comps[:,i])))
plt.annotate(judge[i],comps[:,i])
plt.gca().spines['right'].set_visible(False)
plt.gca().spines['top'].set_visible(False)
plt.xlim([-1,1])
plt.ylim([-1,1])
plt.show()
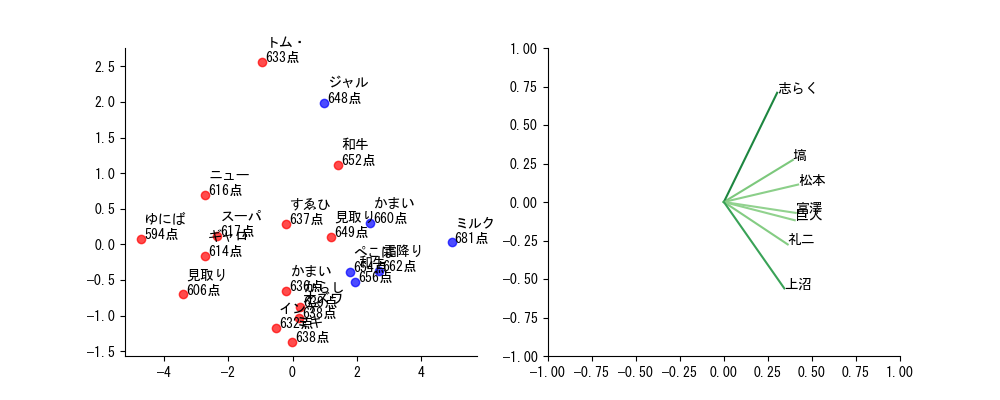
また、これを実行することで得られるグラフは以下の通りです。
少しごちゃっとしていますが、左側の各点にコンビ名の上から3文字と合計得点を記載してあります。右側には各審査員ごとの審査ベクトルをプロットしています。厳めしそうですが、審査員ごとの評価傾向を表したものだと理解していただければ十分です。
5.考察パート
ここでは得られたグラフから縦軸、横軸が一体何を表しているのかを考察し、この審査員下でのM-1では何が評価されているのか分析していきます!
5.1. 第1主成分(横軸)
右側のグラフを見ると、横軸に関して全審査員が同じ方向(右側)を向いていることがわかります。つまり、この評価基準は全審査員に共通しているわけです。実際左側の散布図を見ると、右側にいるコンビのほうが得点の合計が高い傾向にあることが読み取れます。
漫才の審査で全審査員が共通で評価する者と言えば、「面白さ」以外にないわけですから、横軸は面白さを表していると考えるのが一見すると良さそうです。
しかし、本当にそうでしょうか?
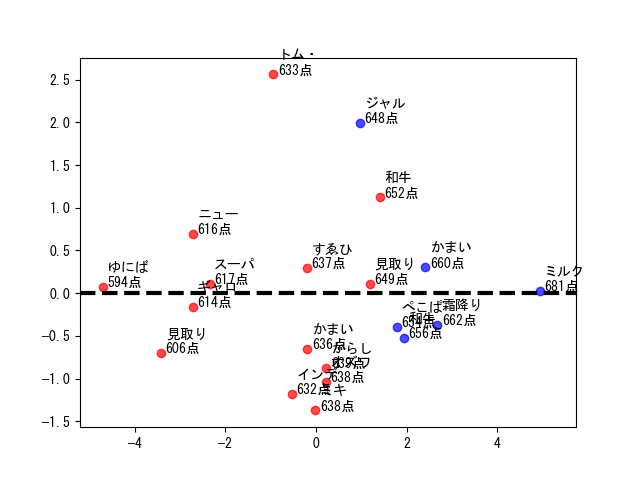
そもそもM-1の決勝に出ておられるコンビが面白くないわけがないですし、「面白さ」は抽象的すぎます。もう少し言語化するために、第2主成分(縦軸)が$0.0$ あたりのデータを見てみます(下図)。
(黒い点線が$0.0$の基準線です。この付近にデータが多いためこの辺りを見ます。)
右から見ていくと、ミルクボーイ、霜降り明星、かまいたち(2019)、和牛(2018)、ぺこぱ... とオールスターのようなコンビが続きます。彼等のM-1での漫才に共通する要素が横軸だと考えるのが自然です。漫才を繰り返し見るとそれが「爆発度」であると考察できます。限られた4分で爆発を起こせるかどうか、これを審査員は評価していると考えると言えるでしょう。
5.2.第2主成分(縦軸)
第1主成分とは違い、審査員の評価ベクトルは縦軸に関してバラバラです。この成分が何を示しているか理解するために、上側2組、トム・ブラウンとジャルジャルの漫才に共通する要素を考えてみます。この2組のネタにはどちらも"フリオチ"といった要素はほぼありません。「最強の中島くん」を作ったり、ひたすら「国名をわけっこ」したりと、混沌としたまま、よくわからないまま面白い漫才だと言えます。
一方、下側のコンビはしっかりと漫才のフォーマットに則っていると考えられます。ぺこぱやミルクボーイはあくまでフォーマットを開発したわけで、そこにはしっかりと理路整然とした漫才の構造があります。すゑひろがりずも一見すると奇抜ですが、しっかりと漫才的なネタになっていると言えます。
以上のことから第2主成分は「漫才度」を示していると言えるでしょう。上に行くほど漫才のフォーマットに則っておらず、下にいくほど"漫才感"があるネタだと推測されます。
5.3. 「上位ゾーン」
ところで、左側のグラフをよく見ると、ジャルジャルを除くファイナルラウンドに出場した5組が右下に固まって位置していることに気づきます。以下ではこれを「上位ゾーン」と呼ぶことにします。上位ゾーンは、先ほど分析に基づけば「爆発力があり、かつ漫才感も残っている」ゾーンだと言い換えることができます。少なくとも2020年のM-1決勝においては、このゾーンに入るようなネタをしたコンビが上位に行くと考えてよいでしょう。
6 おわりに
以上の分析から、この審査員下のM-1では第1に「爆発度」、第2に「漫才度」が重要視されており、これらの評価を満たすような漫才をしたコンビが上位に行くであろうと考えられます。タイトル倒しな、「みんな知ってるよ!」と言われかねない結果となってしまい申し訳ないです。ですが、今までみんなが感覚的に理解していたことを今回データで裏付けられたのであれば、十分意義があるものになったと思います。M-1まであと1週間です!なんとか、なんとかニューヨークに頑張って欲しいです。
京大アドカレなのに京大成分が全くない記事になってしまって申し訳ないです。冒頭にも書いたように現在競プロとkaggleにハマっており、お話できる方を探しています。もちろん自分からも積極的に話しかけにいくので、どうか仲良くしてください。(Twitterはコレ)
明日はUzuraさんが書いてくださります。楽しみです!!
ここまで読んでいただいてありがとうございました!
7. 参考資料
・主成分分析で振り返るM-1グランプリ
・データで見るM1グランプリ2017 〜本当に一番面白かったのはどの漫才だったのか〜
8. おまけ
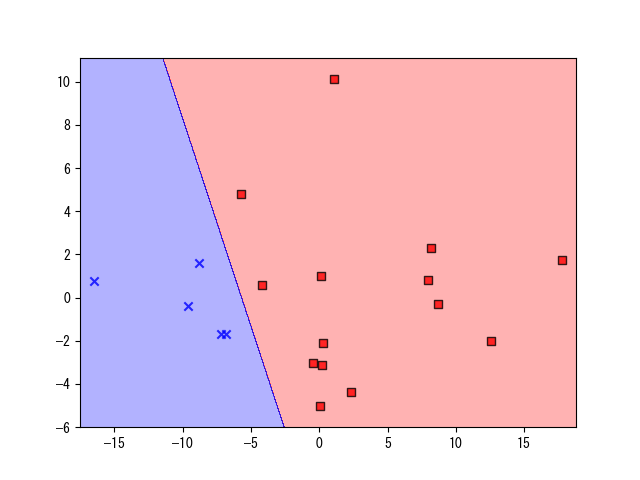
2値分類できそうなデータですが、いかんせんサンプル数が少ないので...。
遊びでロジスティック回帰をかけてみました。今回、ただでさえデータは少ないですが、ジャルジャルは外れ値と見なし取り除いてあります。以下に記すのは標準入力で審査員の点数を入力すると、「どちらに分類されるか」と「それぞれに分類される確率」を返してくれるプログラムです。
気が向いたらM-1のお供としてご利用ください。
import pandas as pd
import numpy as np
from sklearn.decomposition import PCA
df_2018 = pd.read_csv('./M1_2018_.csv')
df_2019 = pd.read_csv('./M1_2019_.csv')
df_2018.columns = ['コンビ名','巨人','礼二','塙','志らく','富澤','松本','上沼','順位']
df_2019.columns = ['コンビ名','巨人','礼二','塙','志らく','富澤','松本','上沼','順位']
judge = ['巨人','礼二','塙','志らく','富澤','松本','上沼']
col = ['コンビ名','巨人','礼二','塙','志らく','富澤','松本','上沼','順位']
df = pd.merge(df_2018,df_2019,on=col,how='outer')
df = df.drop(2,axis=0)
X = df[judge].values
y0 = df["順位"].values
y = [0]*len(y0)
for i in range(len(y0)):
if y0[i] <= 3:
y[i] = 1
else:
y[i] = 0
y = np.array(y)
from sklearn.linear_model import LogisticRegression
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
lr = LogisticRegression(C=10)
lr.fit(X_pca,y)
X = [0]*7
for i in range(7):
X[i] = int(input(judge[i]+'の得点: '))
X = np.array([X])
ya = lr.predict(X)
y_prob = lr.predict_proba(X)
print(ya[0])
for i in range(2):
print(str(i)+"'s probability is:" +' '+str(y_prob[0][i]*100) + '%')
ちなみに決定領域は以下の図のようになります(青がファイナルステージ進出、赤が非進出)