主成分分析で振り返るM-1グランプリ

1. はじめに

M-1グランプリとは，吉本興業が主催する日本最大級の漫才コンテストです．出場資格や採点制度がシビアであること，また結果がテレビ露出に大きな影響を与えるためことが特徴で，漫才大会とは思えない異様な緊張感を持っています．

先週，M-1グランプリ2017が開催され，予選を勝ち上がった10組による決勝ファーストラウンドと，その上位3組による最終決戦が生放送されました．過去の事例を考慮すると，優勝したとろサーモンはもちろん，最終決戦に進出した和牛やミキは，今後テレビ露出が激増することが予想されます．つまり，決勝ファーストラウンドを勝ち抜けるかどうかが今後の人生を左右するとも言えます．

そこで本記事では，データで見る世界，データで見るM1グランプリ2017　〜本当に一番面白かったのはどの漫才だったのか〜¹を参考に，M-1グランプリ2017の決勝ファーストラウンドを主成分分析し，最終決戦進出を分けた要因の考察に挑戦します．分析にはscikit-learnを用います．アドベントカレンダーの趣旨に則り，主成分分析の理論的背景もきちんとご紹介するつもりです．

本記事はM-1グランプリの審査方針について意見を述べるものではなく，いかなる審査結果の不当性を訴えるものではありません．いつも面白い番組を作ってくださり，ありがとうございます！来年も楽しみです．

2. M-1グランプリ2017

本章では，先週行われたM-1グランプリ2017のシステムご紹介します．

2.1 概要

M-1グランプリ2017では，(1)予選，(2)敗者復活戦，(3)決勝ファーストラウンド，そして(4)最終決戦を行い，優勝者を決定します．決勝ファーストラウンドでは，予選および敗者復活戦を勝ち上がった出場者10組が順番にネタを行います．そして，7人の審査員が100点満点で採点し，合計点が大きい上位3組が最終決戦に進出します．

2.2 出場者

出場者は以下の10組です．出身はWikipediaを参考にしました．

• とろサーモン（よしもとクリエイティブ・エージェンシー東京）
• 和牛（よしもとクリエイティブ・エージェンシー大阪）
• ミキ（よしもとクリエイティブ・エージェンシー大阪）
• かまいたち（よしもとクリエイティブ・エージェンシー大阪）
• スーパーマラドーナ（よしもとクリエイティブ・エージェンシー大阪）
• ジャルジャル（よしもとクリエイティブ・エージェンシー東京）
• さや香（よしもとクリエイティブ・エージェンシー大阪）
• ゆにばーす（よしもとクリエイティブ・エージェンシー東京）
• カミナリ（グレープカンパニー）
• マヂカルラブリー（よしもとクリエイティブ・エージェンシー東京）

2.3 審査員

審査員は以下の7名です（敬称略）．出身はWikipediaを参考にしました．

• 上沼恵美子（上沼事務所）
• 松本人志（よしもとクリエイティブ・エージェンシー東京）
• 博多大吉（よしもとクリエイティブ・エージェンシー）
• 春風亭小朝（落語協会）
• 中川家・礼二（よしもとクリエイティブ・エージェンシー）
• 渡辺正行（なべや）
• オール巨人（吉本興業大阪本社）

2.4 採点結果

以下は採点結果です（敬称略）．各列は審査委員の採点と審査結果を示します．

出場者名	上沼	松本	大吉	小朝	礼二	渡辺	巨人	結果
とろサーモン	93	92	93	93	93	93	88	通過
和牛	95	93	94	94	93	92	92	通過
ミキ	95	94	91	92	91	94	93	通過
かまいたち	89	91	92	90	94	89	95	敗退
スーパーマラドーナ	89	90	93	91	92	91	94	敗退
ジャルジャル	90	95	91	90	89	88	93	敗退
さや香	90	90	90	90	90	91	87	敗退
ゆにばーす	90	87	92	91	90	87	89	敗退
カミナリ	90	85	91	90	89	86	87	敗退
マヂカルラブリー	83	84	88	89	88	89	86	敗退

seabornのpairplotで描画すると，下図のようになります．

赤色の点は審査を通過した出場者を表し，緑色の点は敗退した出場者を表します．この図から，審査員個別の評価傾向を理解できますが，全体傾向を把握するのは難しいです．そこで主成分分析と呼ばれるテクニックを使い，情報を二次元に圧縮して可視化してみます．

3. 主成分分析

主成分分析（PCA: Principle Component Analysis）とは，次元削減，非可逆データ圧縮，特徴抽出，データの可視化などに広く適用される手法です．本章では主成分分析を用いてM-1グランプリ決勝の採点結果を可視化します．

3.1 理論

PRMLの12章では，主成分分析の導出方法が三種類述べられています．

1. 分散最大化による導出．
2. 誤差最小化による導出．
3. 線形ガウスモデルを仮定した最尤法による導出（確率的主成分分析とも呼ばれます）．

1については，本アドベントカレンダーの一日目で@NoriakiOshitaさんが意味がわかる主成分分析を書いてくださいました．本記事では2についてご紹介します．3については，PRMLの12章をご参照ください．

まず，データ$\boldsymbol{x}_n$（n=1, 2, ..., N）を完全正規直交系$\boldsymbol{u}_i$（i=1, 2, ..., D）で表現することを考えます．ここで，Nはデータの数（M-1グランプリ2017では10）Dはもともとのデータの次元数（M-1グランプリ2017では7）を表します．

 \boldsymbol{x}_n = \sum_{i} \alpha_{ni} \boldsymbol{u}_i 

ここで上式と$\boldsymbol{u}_j$の内積を取ると，直交性から

 \boldsymbol{x}_n^T \boldsymbol{u}_j = \sum_{i} \alpha_{ni} \boldsymbol{u}_i^T \boldsymbol{u}_j = \alpha_{nj} 

を得ます．これをもとの式に代入して$\alpha$を消去すると，下式を得ます．

 \boldsymbol{x}_n = \sum_{i} (\boldsymbol{x}_n^T \boldsymbol{u}_j) \boldsymbol{u}_i 

次に，$M$個の変数（$M<D$）でデータ点を近似することを考えます．つまり：

 \tilde{\boldsymbol{x}}_n = \sum_{i=1}^{M} z_{ni} \boldsymbol{u}_i +  \sum_{i=M+1}^{D} b_{i} \boldsymbol{u}_i

$z_{ni}$はデータ点毎に決まる変数ですが，$b_{i}$は全てのデータ点に共通な変数であることに注意してください．下図は，$D=2$かつ$M=1$，つまり二次元データ$\boldsymbol{x}$を直線$l$上に射影する例を表しています．

以下では，最も近似誤差が小さくなるような$z_{ni}$，$b_{i}$および$\boldsymbol{u}_{i}$を計算します．目的関数として歪み尺度$J$を導入します．

J = \frac{1}{N} \sum_{n=1}^{N} \mid \mid \boldsymbol{x}_n - \tilde{\boldsymbol{x}}_n \mid \mid^{2}

$J$を$z_{ni}$で微分して$0$と等しいおくと，下式を得ます．

z_{ni} =\boldsymbol{x}_{n}^{T} \boldsymbol{u}_{i}

上図では，データ点を直線$l$に垂直に射影するとき，$J$が最も小さくなることを意味します．同様に，$J$を$b_{i}$で微分して$0$と等しいおくと，下式を得ます．

b_{i} =\bar{\boldsymbol{x}}^{T} \boldsymbol{u}_{i}

ここで$\bar{\boldsymbol{x}}=\frac{1}{N} \sum_{n} \boldsymbol{x}_{n}$です．上図では，データ点の平均を通るよう直線$l$を引くとき，$J$が最も小さくなることを意味します．以上から，歪み尺度$J$を次のように書き直すことができます．

J = \frac{1}{N} \sum_{n=1}^{N} \sum_{i=M+1}^{D} (\boldsymbol{x}_{n}^{T} \boldsymbol{u}_{i} - \bar{\boldsymbol{x}}^{T} \boldsymbol{u}_{i})^{2} 
  = \sum_{i=M+1}^{D} \boldsymbol{u}_{i}^{T} \boldsymbol{S} \boldsymbol{u}_{i} 

ここで

\boldsymbol{S}=\frac{1}{N} \sum_{n} (\boldsymbol{x}_{n} - \bar{\boldsymbol{x}}_{n} )^{T} (\boldsymbol{x}_{n} - \bar{\boldsymbol{x}}_{n} ) 

は写像前の空間における共分散行列を表します．つまり，歪み尺度$J$は，削減されてしまう次元（$i=M+1, ..., D$）に射影された分散の和であることがわかります．

よって，歪み尺度$J$を最小化するためには，できるだけ射影後の分散が大きくなるような軸を，削減せず残す次元（$i=1, ..., M$）として選択する必要があります．これは，共分散行列の固有ベクトルのうち，固有値が大きいものを選択することに相当します．以降はQiita，意味がわかる主成分分析をご参照ください．

3.2 実装

以下の環境で主成分分析を実施しました．

• Ubuntu 16.04
• Python 3.6.2
• NumPy 1.13.1
• Pandas 0.20.3
• Matplotlib 2.0.2
• Scikit-learn 0.19.0

Jupyter notebookはこちらです．遊んで頂けると嬉しいです．

まず，必要なモジュールをインポートします．

import numpy as np
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from sklearn import preprocessing # 前処理用
from sklearn.decomposition import PCA # 主成分分析用

Matplotlibで日本語を表示するために，Qiita，matplotlibで日本語を描画 on Ubuntuを参考に，次のような設定を行います．Ubuntu以外をお使いの場合は，適宜ご対応ください．

from matplotlib.font_manager import FontProperties
font_path = '/usr/share/fonts/truetype/takao-gothic/TakaoPGothic.ttf'
font_prop = FontProperties(fname=font_path)
matplotlib.rcParams['font.family'] = font_prop.get_name()

以降では，data/ディレクトリの2017.csvに採点結果が格納されていると仮定します．データの読み出しから主成分分析結果のプロットまで，一括して実施する関数plot_m1(year)を定義します．4章では過去大会のデータもプロットするので，yearで開催年を指定できるようにします．

def plot_m1(year=2017):
  """
  `data/`ディレクトリにある`year`年の採点結果を読み出し，
  主成分分析結果を描画し，dataframeを返す関数です．
  - year: 分析対象とする大会の開催年．
  """

  # データの読み出し
  df = pd.read_csv("data/{}.csv".format(year))
  x = np.array(df.values)[:, 1:-1]
  t = np.array([1 if i=="通過" else 0 for i in df["結果"].values])
  x_scaled = preprocessing.scale(x) # 正規化
  x_pca = PCA(n_components=2).fit_transform(x_scaled)
  # 主成分空間に射影

  plt.figure(figsize=[10, 4])

  # 主成分空間で出場者をプロット．
  plt.subplot(1, 2, 1)
  for ii in range(len(t)):
      plt.plot(x_pca[ii, 0], x_pca[ii, 1],
               c= 'b' if t[ii] else 'r', marker='o', alpha=0.7)
      plt.annotate(
          "{}\n{}点".format(df.iloc[ii, 0][:3], sum(df.iloc[ii, 1:-1])),
          x_pca[ii]+[.1, 0])
  plt.xlim([min(x_pca[:, 0])-.5, max(x_pca[:, 0])+.8])
  plt.gca().spines['right'].set_visible(False)
  plt.gca().spines['top'].set_visible(False)

  # 主成分空間で審査員をプロット．
  plt.subplot(1, 2, 2)
  judge = df.columns[1:-1]
  comps = PCA(n_components=2).fit(x_scaled).components_
  for ii in range(len(judge)):
      plt.plot([0, comps[0, ii]], [0, comps[1, ii]],
                c=cm.Greens(np.linalg.norm(comps[:, ii])))
      plt.annotate(judge[ii], comps[:, ii])
  plt.gca().spines['right'].set_visible(False)
  plt.gca().spines['top'].set_visible(False)
  plt.xlim([-1, 1]), plt.ylim([-1, 1])

  return df

sklearn.decomposition.PCAクラスでは，引数n_componentsで主成分空間の次元数を指定できます．今回は可視化が目的なので，2を指定します．fit_transform()メソッドは，主成分空間の射影結果を返す関数です．

3.3 結果と考察

以下を実行して，採点結果を可視化します．

plot_m1()

両図ともに，横軸は第一主成分，縦軸は第二主成分です．左図は主成分空間における各出場者の分布を表します．青点は最終決戦進出，赤点は敗退を表します．一方，右図は主成分空間における各審査員の評価傾向を表します．近くに位置する審査員同士は，似たような評価傾向を持ちます．例えば，オール巨人さんに強く支持された出場者は，左図の左上付近に分布する傾向があります．一方で小朝さんに強く支持された出場者は，左図の左下付近に分布する傾向があります．

第一主成分（横軸）に注目すると，全審査員に共通する評価傾向がある ことがわかります．左側に位置する出場者ほど，全ての審査員が面白いと判断したようです．

次に，第二主成分（縦軸）に注目すると，審査員は三つのクラスタに分類できることがわかります．

• 左下方向を強く評価する，非吉本クラスタ（上沼さん，小朝さん，渡辺さん）
• 左やや上方向を強く評価する，吉本プレーヤークラスタ（松本さん，礼二さん，大吉さん）
• 左上方向を強く評価する，吉本ベテランクラスタ（巨人さん）

非吉本クラスタと吉本ベテランクラスタの評価傾向は大きく異なり，吉本プレーヤークラスタはその中間付近に位置しています．ここで注意して頂きたいのは，非吉本クラスタは3人で構成されているのに対し，吉本ベテランクラスタは1人で構成されていることです．つまり，非吉本クラスタに支持された出場者のほうが，吉本ベテランクラスタに支持された出場者よりも総合点が高くなり，最終決戦に進出しやすかったのではないかと推測できます．あくまでも結果論ですが．

より踏み込んだ議論については，データで見る世界，データで見るM1グランプリ2017　〜本当に一番面白かったのはどの漫才だったのか〜をご参照ください．

4. 過去の大会

せっかくなので，過去の大会も同様にプロットしてみます．時間が足りず考察はできませんでしたが，結果を眺めるだけでもお楽しみいただけるかと思います．なお，大会によって細かなルールが異なる場合がありますので，詳細はWikipediaをご参照ください．

第1回（2001年）

plot_m1(2001)

出場者名	紳助	松本	鴻上	石井	小朝	青島	きよし	札幌	大阪	福岡	結果
中川家	80	70	85	90	90	90	91	65	89	79	通過
ハリガネロック	75	60	85	92	70	90	95	85	85	72	通過
アメリカザリガニ	74	65	84	92	80	85	88	84	57	87	敗退
ますだおかだ	78	70	84	88	80	80	95	75	52	68	敗退
麒麟	75	75	83	90	65	75	79	54	82	63	敗退
フットボールアワー	66	55	82	82	80	80	90	62	83	46	敗退
キングコング	74	55	83	76	70	75	95	64	55	60	敗退
チュートリアル	60	50	75	68	75	75	80	38	67	49	敗退
DonDokoDon	64	65	84	82	65	85	75	47	18	29	敗退
おぎやはぎ	50	60	73	82	75	80	77	22	9	12	敗退

第2回（2002年）

plot_m1(2002)

出場者名	紳助	松本	大竹	石井	洋七	カウス	談志	結果
ますだおかだ	89	70	92	90	96	95	80	通過
フットボールアワー	89	85	91	95	94	97	70	通過
笑い飯	86	80	80	84	84	83	70	通過
おぎやはぎ	76	80	79	79	85	82	80	敗退
ハリガネロック	75	65	83	81	86	85	70	敗退
テツandトモ	76	65	77	82	79	90	70	敗退
スピードワゴン	73	75	80	86	86	85	50	敗退
ダイノジ	83	60	78	78	81	84	70	敗退
アメリカザリガニ	73	60	78	78	83	83	70	敗退

第3回（2003年）

plot_m1(2003)

出場者名	紳助	松本	南原	洋七	石井	大竹	カウス	結果
フットボールアワー	98	97	89	97	95	89	98	通過
笑い飯	99	95	90	95	92	90	95	通過
アンタッチャブル	92	84	85	90	92	87	86	通過
2丁拳銃	91	80	87	95	86	83	86	敗退
りあるキッズ	90	85	81	93	85	83	84	敗退
スピードワゴン	85	74	81	85	86	82	79	敗退
アメリカザリガニ	80	70	84	90	83	76	81	敗退
麒麟	84	75	76	84	78	75	82	敗退
千鳥	82	70	82	75	84	79	80	敗退

第4回（2004年）

plot_m1(2004)

出場者名	きよし	南原	大竹	洋七	小朝	石井	カウス	結果
アンタッチャブル	97	96	95	97	95	96	97	通過
南海キャンディーズ	90	92	86	92	90	95	94	通過
麒麟	89	88	89	92	88	92	96	通過
タカアンドトシ	86	86	82	91	85	90	95	敗退
笑い飯	84	89	82	91	85	89	95	敗退
POISON GIRL BAND	87	85	83	81	88	89	90	敗退
トータルテンボス	80	84	79	84	84	88	88	敗退
東京ダイナマイト	82	80	76	83	87	86	89	敗退
千鳥	83	83	81	78	82	82	93	敗退

第5回（2005年）

plot_m1(2005)

出場者名	紳助	松本	渡辺	大竹	洋七	石井	カウス	結果
ブラックマヨネーズ	95	95	93	90	96	94	96	通過
笑い飯	85	95	90	85	91	92	95	通過
麒麟	88	90	91	90	95	95	97	通過
品川庄司	85	90	87	89	95	91	89	敗退
チュートリアル	85	95	86	84	86	95	91	敗退
千鳥	82	80	89	88	86	89	93	敗退
タイムマシーン3号	76	75	83	82	82	85	88	敗退
アジアン	75	70	80	82	81	86	90	敗退
南海キャンディーズ	72	75	79	79	79	80	88	敗退

第6回（2006年）

plot_m1(2006)

出場者名	紳助	松本	南原	渡辺	洋七	大竹	カウス	結果
チュートリアル	97	95	95	90	98	92	97	通過
フットボールアワー	90	90	94	90	91	89	96	通過
麒麟	88	87	91	89	92	86	94	通過
笑い飯	89	89	92	85	90	89	92	敗退
トータルテンボス	87	90	88	85	90	83	90	敗退
ライセンス	85	85	90	88	89	83	89	敗退
ザ・プラン9	83	80	89	80	90	82	93	敗退
変ホ長調	82	75	84	79	85	83	88	敗退
POISON GIRL BAND	76	85	85	75	81	83	85	敗退

第7回（2007年）

plot_m1(2007)

出場者名	紳助	松本	上沼	石井	巨人	大竹	カウス	結果
サンドウィッチマン	98	95	95	95	92	84	92	通過
トータルテンボス	96	93	95	95	90	84	93	通過
キングコング	96	93	97	95	88	90	91	通過
ハリセンボン	86	88	93	84	86	85	86	敗退
笑い飯	85	85	89	85	83	85	92	敗退
ザブングル	86	90	92	84	79	84	82	敗退
ダイアン	86	85	89	86	81	82	84	敗退
千鳥	86	80	85	80	87	81	81	敗退
POISON GIRL BAND	75	90	81	82	84	80	85	敗退

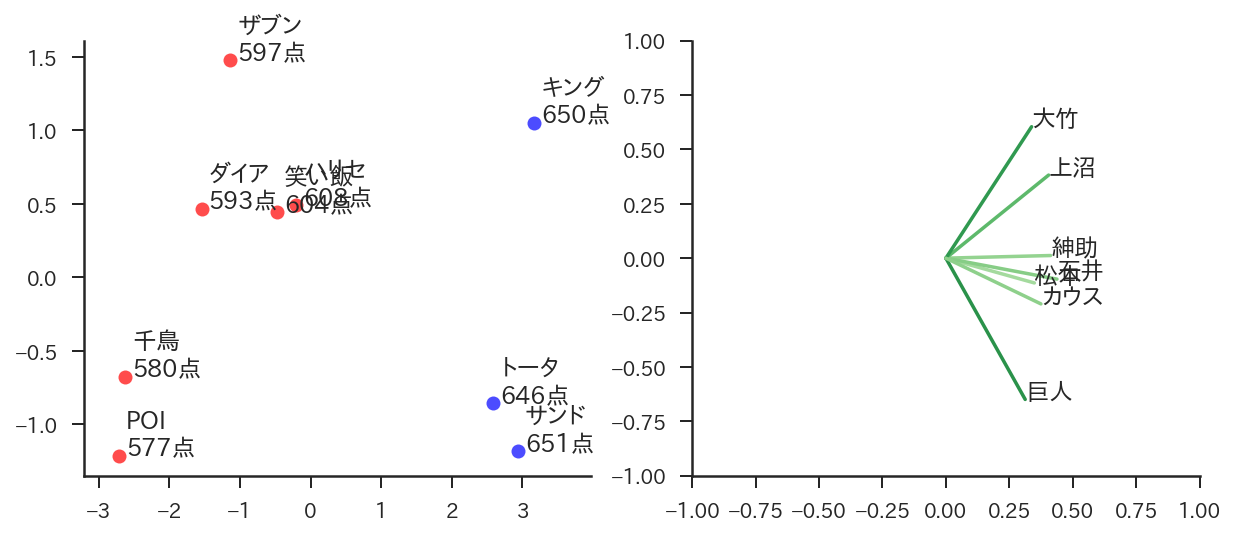
第8回（2008年）

plot_m1(2008)

出場者名	紳助	松本	上沼	渡辺	巨人	大竹	カウス	結果
NON STYLE	94	93	95	90	91	90	91	通過
オードリー	89	95	92	92	91	92	98	通過
ナイツ	89	93	95	91	89	89	94	通過
笑い飯	95	89	95	91	91	88	88	敗退
U字工事	91	85	93	90	84	88	92	敗退
ダイアン	89	85	90	90	86	86	93	敗退
モンスターエンジン	91	83	85	88	89	88	90	敗退
キングコング	88	86	90	89	86	87	86	敗退
ザ・パンチ	87	80	88	85	83	83	85	敗退

第9回（2009年）

plot_m1(2009)

出場者名	紳助	松本	上沼	東国原	巨人	渡辺	カウス	結果
パンクブーブー	94	93	98	88	90	91	97	通過
笑い飯	100	95	98	92	93	92	98	通過
NON STYLE	90	92	98	89	87	90	95	通過
ナイツ	91	85	93	88	90	91	96	敗退
ハライチ	90	88	91	86	89	89	95	敗退
東京ダイナマイト	85	88	90	85	86	90	90	敗退
モンスターエンジン	89	83	90	85	87	89	87	敗退
南海キャンディーズ	85	83	90	89	84	88	88	敗退
ハリセンボン	82	80	87	87	85	85	89	敗退

第10回（2010年）

plot_m1(2010)

出場者名	紳助	松本	南原	大竹	渡辺	宮迫	カウス	結果
笑い飯	96	96	98	97	90	95	96	通過
スリムクラブ	91	96	93	91	88	91	94	通過
パンクブーブー	97	97	94	91	95	98	96	通過
ピース	88	89	87	89	89	92	95	敗退
銀シャリ	87	90	89	89	87	93	92	敗退
ナイツ	92	88	90	90	88	91	87	敗退
ハライチ	87	86	89	90	90	90	88	敗退
ジャルジャル	86	87	88	89	87	90	79	敗退
カナリア	81	85	86	87	85	88	80	敗退

第11回（2015年）

plot_m1(2015)

出場者名	礼二	増田	岩尾	吉田	徳井	富澤	石田	佐藤	哲夫	結果
トレンディエンジェル	94	93	89	93	88	93	92	92	91	通過
銀シャリ	91	91	92	89	95	92	87	89	92	通過
ジャルジャル	89	89	96	90	96	94	94	93	93	通過
タイムマシーン3号	93	90	90	89	88	93	94	91	88	敗退
スーパーマラドーナ	92	87	93	90	89	91	88	93	90	敗退
和牛	90	92	92	86	90	90	88	90	88	敗退
メイプル超合金	87	85	89	85	91	92	89	89	89	敗退
馬鹿よ貴方は	88	85	90	83	89	93	83	90	90	敗退
ハライチ	92	89	85	83	89	89	86	88	87	敗退

第12回（2016年）

plot_m1(2016)

出場者名	上沼	松本	大吉	礼二	巨人	結果
銀シャリ	95	95	93	91	96	通過
和牛	95	93	91	95	95	通過
スーパーマラドーナ	93	89	92	95	90	通過
さらば青春の光	91	90	90	90	87	敗退
アキナ	89	87	89	89	92	敗退
ハライチ	93	85	89	88	91	敗退
カミナリ	81	89	90	90	91	敗退
スリムクラブ	89	90	88	89	85	敗退
相席スタート	90	84	87	88	87	敗退

5. おわりに

M-1グランプリの決勝ファーストラウンドの採点結果を主成分分析してみました．審査員は，それぞれに嗜好を出しつつ，納得感のある採点を行っていることがわかりました．これはとても大変な仕事だと思います²．

最後まで読んでくださり，ありがとうございました！

6. 参考

• M-1グランプリ公式サイト
• Wikipedia，M-1グランプリ
• P.M.ビショップ，パターン認識と機械学習
• Qiita，意味がわかる主成分分析
• Qiita，matplotlibで日本語を描画 on Ubuntu
• データで見る世界，データで見るM1グランプリ2017　〜本当に一番面白かったのはどの漫才だったのか〜

---

1. 審査員の分析だけでなく，Twitterでお茶の間の反応も分析した，素晴らしい記事です． ↩

2. 少なくとも私にはできません． ↩