はじめに
機械学習(主にディープラーニング)の性能評価の指標としてAccuracy(正解率)がよく用いられますが,その他にもPrecision(適合率),Recall(再現率),F-measure(F値)などの評価指標も存在します.例えば10クラス分類問題で,以下の表の様なデータ数のデータセットを利用して学習することを考えます.
| class | percentage | class | percentage |
|---|---|---|---|
| 0 | 91% | 5 | 1% |
| 1 | 1% | 6 | 1% |
| 2 | 1% | 7 | 1% |
| 3 | 1% | 8 | 1% |
| 4 | 1% | 9 | 1% |
これは極端な例ですが,モデルが全て0を出力するだけでAccuracyが91%になります.全く分類ができていないにも関わらず,Accuracyの値が大きくなってしまうため,Accuracyでモデルの性能を評価することは不適切だと分かります.この様に,クラスごとのデータ数に偏りがある場合には,Precision,Recall,F-measure等の他の評価指標も用いる必要があります.
この記事では,KerasのmetricsでAccuracy以外の評価指標を利用する方法について説明します.対象とする評価基準は以下の通りです.
- クラスごとのAccuracy/Precision/Recall/F-measure
- Micro Precision/Micro Recall/Micro F-measure/Average Accuracy
- Macro Precision/Macro Recall/Macro F-measure
このブログでの解説を参考にしました.機械学習で使う指標総まとめ(教師あり学習編)
ソースコードはこちらからどうぞ.
環境
| version | |
|---|---|
| Python | 3.5.5 |
| Keras | 2.1.6 |
| TensorFlow | 1.8.0 |
| TensorBoard | 1.8.0 |
注意(2018/12/27追記)
この記事で解説しているmetricsは近似値で,必ずしも正しい値ではありません.バッチサイズが小さいほど誤差が大きくなる可能性が高いです.Kerasの公式にも以前はPrecision等のmetricsがあったのですが,この記事で解説しているmetricsと同様に近似値の計算となっていたため削除されたようです.
正確な値を計算したい場合はこちらのIssueにあるように,毎エポック終了時のコールバックを利用して,全データセットに対する計算すると良いと思います.
@yakigacさん,ご指摘ありがとうございました.
metrics
KerasのModelをcompileする際の引数にmetricsというものがあり,評価関数のリストを渡してあげることで,学習の中でその評価が行われ,TensorBoardなどで出力することが可能になります.Kerasで用意されている評価関数には,accuracyやmean_squared_errorなどがありますが,自身で作成することもできます.正解ラベルのテンソルと予測ラベルのテンソルの2つを引数とし,評価値のスカラーまたはテンソルを返す関数をmetricsのリストに加えることで,オリジナルの評価関数を利用することができます.Kerasのドキュメントでは,モデルの予測値の平均値を評価値とする,評価関数の例が示されています.
import keras.backend as K
def mean_pred(y_true, y_pred):
return K.mean(y_pred)
model.compile(optimizer='rmsprop',
loss='binary_crossentropy',
metrics=['accuracy', mean_pred])
引数のy_trueとy_predがバッチサイズを含めたshapeのテンソルとして渡されるため,keras.backendを用いて評価値を計算しています.
準備
2クラス分類問題では,モデルの予測と正解のデータの4種類の組み合わせにそれぞれ名前がついています.
| 予測\正解 | ○ | × |
|---|---|---|
| ○ | True Positive(TP:真陽性) | False Positive(FP:偽陽性) |
| × | False Negative(FN:偽陰性) | True Negative(TN:真陰性) |
PrecisionとRecallはこの4種類の値を利用した条件付き確率として計算され,F-measureはPrecisionとRecallを利用して計算されます.そして,これらの概念は多クラス分類問題にも適用することができます.この中で個別に計算する必要がある値はTrue Positiveだけなので,まずはその値を計算する関数を作成します.これ以下のコードでは,imoprtが行われていることとします.
from functools import partial
import keras.backend as K
from keras.callbacks import TensorBoard
from keras.datasets import mnist
from keras.layers import Input, Dense
from keras.models import Model
from keras.utils import to_categorical
y_predの正規化
引数のy_predはモデルの出力がそのまま渡されるため,y_trueと次元が一致しません.そのため,y_predの値をone hotベクトルに変換します.
def normalize_y_pred(y_pred):
return K.one_hot(K.argmax(y_pred), y_pred.shape[-1])
True Positive
クラスごとのTrue Positiveと全体のTrue Positiveを計算します.
def class_true_positive(class_label, y_true, y_pred):
y_pred = normalize_y_pred(y_pred)
return K.cast(K.equal(y_true[:, class_label] + y_pred[:, class_label], 2),
K.floatx())
def true_positive(y_true, y_pred):
y_pred = normalize_y_pred(y_pred)
return K.cast(K.equal(y_true + y_pred, 2),
K.floatx())
クラスごとのTrue Positiveは,スライスを利用して([:, class_label])特定のクラスの列を抽出しています.クラスごとに必要な評価関数を定義していくとソースコードが冗長になってしまうため,対象とするクラスラベル・y_true・y_predを引数とする関数に,クラスラベルの引数を部分適用して利用します.
MicroとMacro
Microはクラス全体で計算するの対して,MacroではクラスごとのPrecision,Recall,F-measureを計算した後にそれらの平均値を取ります.こうすることで,各クラスの影響をデータ数に関係なく等しく扱うことができるようになります.また,Accuracyに関しては,Overall AccuracyとAverage AccuracyがMicroとMacroにそれぞれ対応します.
他クラス分類問題においては,Micro ~とOverall Accuracy,Macro RecallとAverage Accuracyが同じ値になりますが,一応全ての評価関数を作成したいと思います.
Precision
Precisionはモデルのあるクラスの予測のうち,正解と一致した割合です.
$$Precision=\frac{TP}{TP+FP}=\frac{TP}{モデルがあるクラスを予測した数}$$
def class_precision(class_label, y_true, y_pred):
y_pred = normalize_y_pred(y_pred)
return K.sum(class_true_positive(class_label, y_true, y_pred)) / (K.sum(y_pred[:, class_label]) + K.epsilon())
def micro_precision(y_true, y_pred):
y_pred = normalize_y_pred(y_pred)
return K.sum(true_positive(y_true, y_pred)) / (K.sum(y_pred) + K.epsilon())
def macro_precision(y_true, y_pred):
class_count = y_pred.shape[-1]
return K.sum([class_precision(i, y_true, y_pred) for i in range(class_count)]) \
/ K.cast(class_count, K.floatx())
Recall
Recallはあるクラスの正解のうち,モデルの予測と一致した割合です.
$$Recall=\frac{TP}{TP+FN}=\frac{TP}{あるクラスの正解の数}$$
def class_recall(class_label, y_true, y_pred):
return K.sum(class_true_positive(class_label, y_true, y_pred)) / (K.sum(y_true[:, class_label]) + K.epsilon())
def micro_recall(y_true, y_pred):
return K.sum(true_positive(y_true, y_pred)) / (K.sum(y_true) + K.epsilon())
def macro_recall(y_true, y_pred):
class_count = y_pred.shape[-1]
return K.sum([class_recall(i, y_true, y_pred) for i in range(class_count)]) \
/ K.cast(class_count, K.floatx())
F-measure
F-measureはPrecisionとRecallの調和平均で,2つの指標のバランスを取ったものです.
$$\frac{1}{F-measure}=\frac{1}{2}(\frac{1}{Precision}+\frac{1}{Recall})$$
$$F-measure=\frac{2\cdot Precision\cdot Recall}{Precision+Recall}$$
def class_f_measure(class_label, y_true, y_pred):
precision = class_precision(class_label, y_true, y_pred)
recall = class_recall(class_label, y_true, y_pred)
return (2 * precision * recall) / (precision + recall + K.epsilon())
def micro_f_measure(y_true, y_pred):
precision = micro_precision(y_true, y_pred)
recall = micro_recall(y_true, y_pred)
return (2 * precision * recall) / (precision + recall + K.epsilon())
def macro_f_measure(y_true, y_pred):
precision = macro_precision(y_true, y_pred)
recall = macro_recall(y_true, y_pred)
return (2 * precision * recall) / (precision + recall + K.epsilon())
Accuracy
Accuracyは皆さんご存知の通り,モデルの予測と正解が一致した割合です.
$$Accuracy=\frac{TP+TN}{TP+FP+FN+TN}$$
def class_accuracy(class_label, y_true, y_pred):
y_pred = normalize_y_pred(y_pred)
return K.cast(K.equal(y_true[:, class_label], y_pred[:, class_label]),
K.floatx())
def average_accuracy(y_true, y_pred):
class_count = y_pred.shape[-1]
class_acc_list = [class_accuracy(i, y_true, y_pred) for i in range(class_count)]
class_acc_matrix = K.concatenate(class_acc_list, axis=0)
return K.mean(class_acc_matrix, axis=0)
Overall Accuracyはmetricsにaccuracyを指定した場合に利用できるため,実装は省略します.
部分適用を利用した評価関数の生成
クラスごとの評価関数は引数の条件が合わないため,部分適用をしてy_true,y_predを引数に取る関数を作成する必要があります.Pythonで部分適用をするためにはfunctools.partial()を利用します.部分適用で作成した関数オブジェクトをmetricsで利用するために,__name__属性を付けています(metricsの区別に利用されています).こうすることで,Accuracy,Precision,Recall,F-measureの4種類×10クラス分の関数定義を省略することができました.
def generate_metrics():
metrics = ["accuracy"]
# classごとのmetrics
func_list = [class_accuracy, class_precision, class_recall, class_f_measure]
name_list = ["acc", "precision", "recall", "f_measure"]
for i in range(10):
for func, name in zip(func_list, name_list):
func = partial(func, i)
func.__name__ = "{}-{}".format(name, i)
metrics.append(func)
# 全体のmetrics
metrics.append(average_accuracy)
metrics.append(macro_precision)
metrics.append(macro_recall)
metrics.append(macro_f_measure)
return metrics
TensorBoard
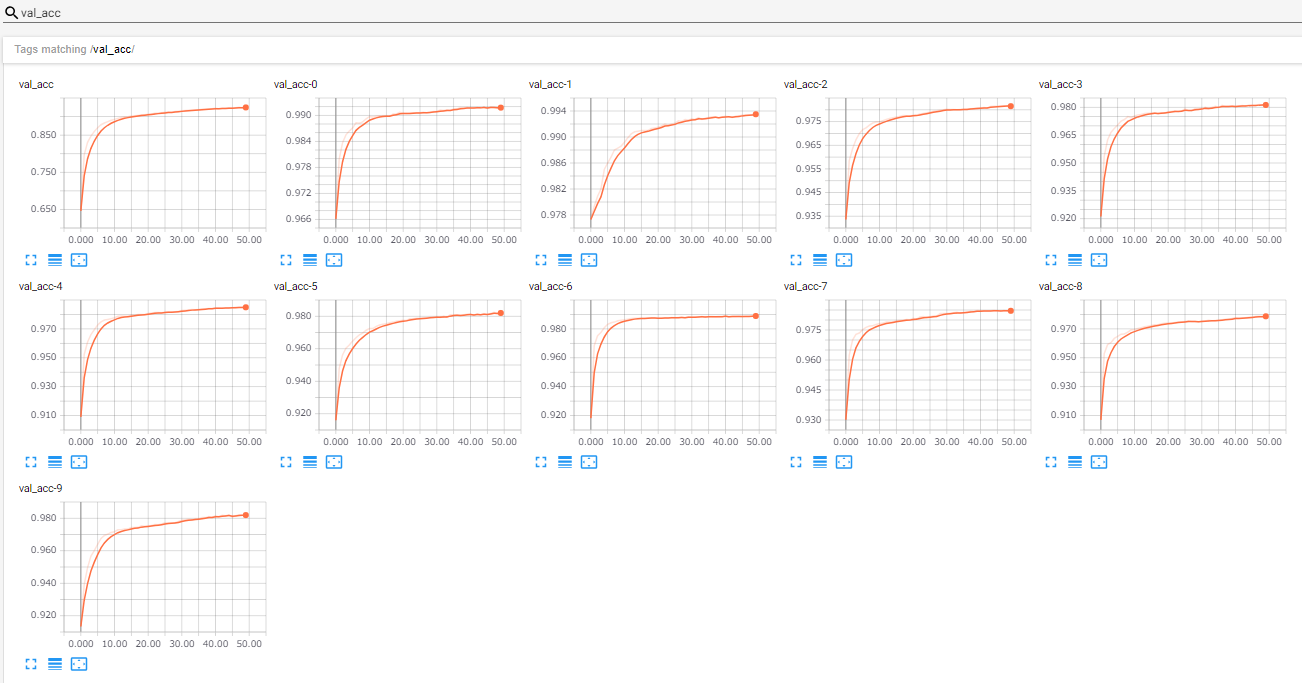
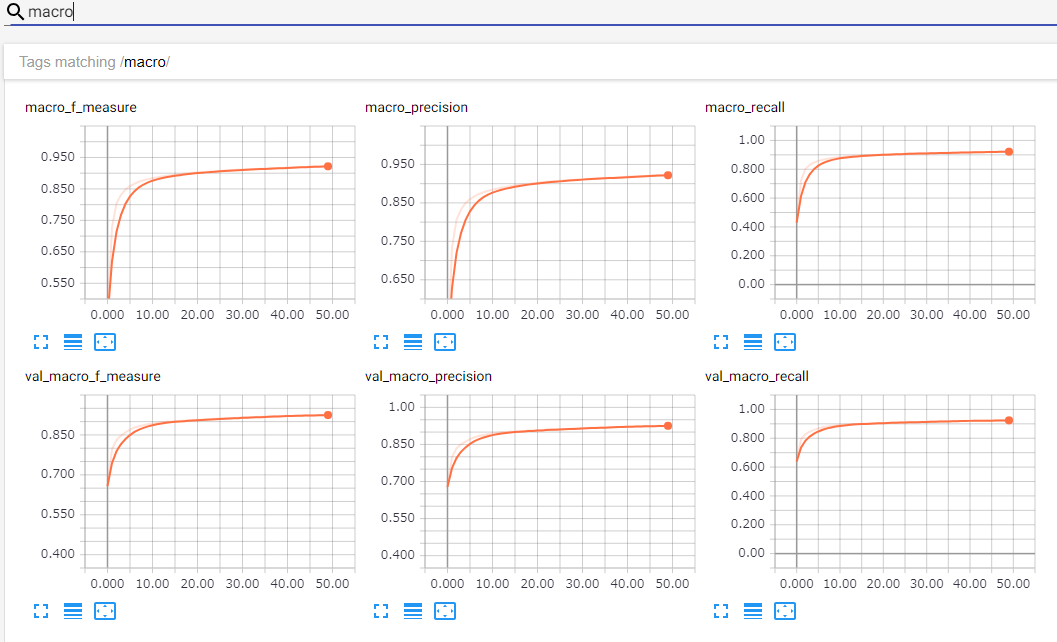
MNISTを利用してTensorBoardのSCALARSを確認したいと思います.
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000, 784) / 255
x_test = x_test.reshape(10000, 784) / 255
y_train = to_categorical(y_train, 10)
y_test = to_categorical(y_test, 10)
inputs = Input(shape=(784,))
x = Dense(32, activation="relu")(inputs)
x = Dense(10, activation="softmax")(x)
model = Model(inputs=inputs, outputs=x)
model.compile(optimizer="SGD",
loss="categorical_crossentropy",
metrics=generate_metrics())
model.fit(x_train, y_train,
validation_data=(x_test, y_test),
batch_size=400,
epochs=50,
callbacks=[TensorBoard()])
クラスごとのAccuracyやMacro Precisionなどがちゃんと表示されていますね!
おわりに
今回はPrecision,Recall,F-measure等の基本的な評価関数を実装しましたが,metricsに渡す関数の形式さえ守れば,どんな評価関数でも利用することができます.TensorBoardは強力な可視化ツールなので,積極的に利用していきたいですね.metricsに渡した評価関数は,fit()などの戻り値であるHistoryオブジェクトにも反映されるので,Matplotlib等で綺麗なグラフを描きたい時にも役立つと思います.