この記事は Qiita p5js アドベントカレンダー8日目の記事です。
これはなに
p5.jsが用意している関数について理解を深める記事です。
今回はMath、Random系に位置するrandomGaussian()について。
randomGaussian()
リファレンスより
ガウス分布(正規分布)に当てはまる乱数を返します。理論的には、randomGaussian()が返す最小値や最大値はありません。むしろ、平均値から遠く離れた値が返される可能性は非常に低く、平均値に近い値が返される可能性は高いと言えます。0、1、2のいずれかの引数を取ります。
引数を取らない場合、平均値0、標準偏差1を返します。
引数が1つの場合、その引数は平均値です(標準偏差は1)。
引数が2つの場合は、1つ目が平均値、2つ目が標準偏差です。
まずガウス分布が分からないので調べました。
こちらの記事の説明がわかりやすかったです。
数学的な部分は一切わかりませんが、「ガウス分布に当てはまる」とは次のことを指すのでしょう。以下記事の抜粋です。
平均値と最頻値と中央値が一致する。
平均値を中心にして左右対称である。(直線𝑥=μに関して対称)
𝑥軸が漸近線である。
分散(標準偏差)が大きくなると、曲線の山は低くなり、左右に広がって平らになる。分散(標準偏差)が小さくなると、山は高くなり、よりとんがった形になる。
つまりrandomGaussian()を使えば、randomの結果をこのルールに乗せることできるというわけですね。
Type
randomGaussian(mean: number, sd: number): number;
引数
- mean randomな数の平均値。ここが最も集合する箇所になる。
- sd 標準偏差の数値。この値が高いほど、より分散する。
どんな時に使えそうか
リファレンスを参考にして、次のコードを書いてみました。
function setup() {
createCanvas(600, 600);
frameRate(20)
}
function draw() {
background(0);
stroke('white')
strokeWeight(1);
for (let x = 0; x < 600; x++) {
const y = randomGaussian(300, 50)
line(x, 300, x, y)
}
}
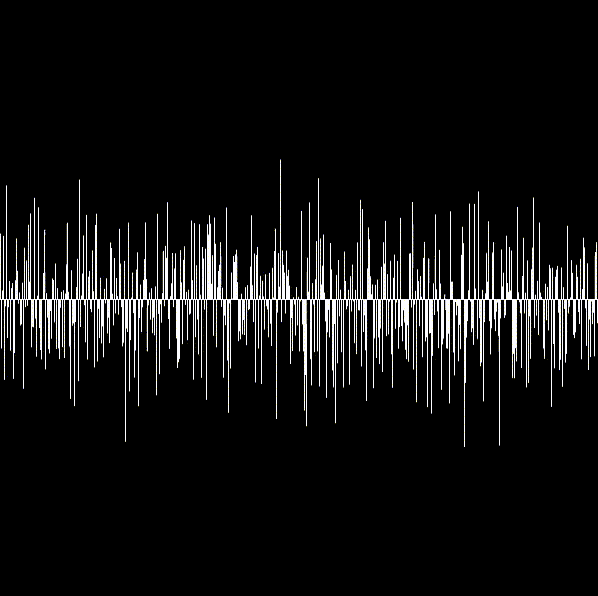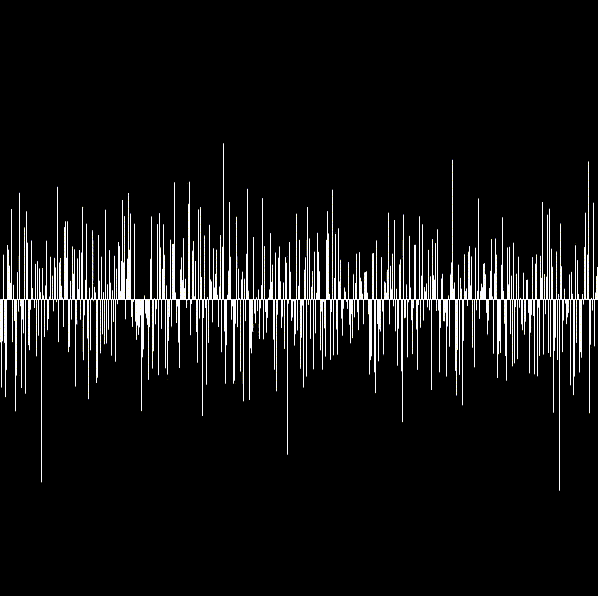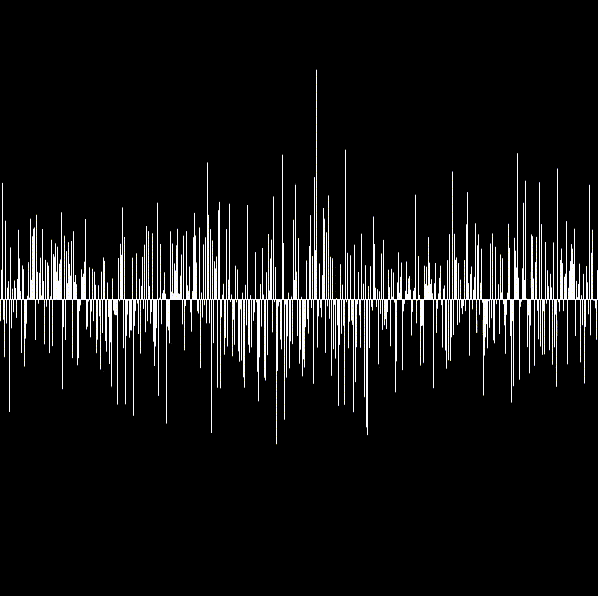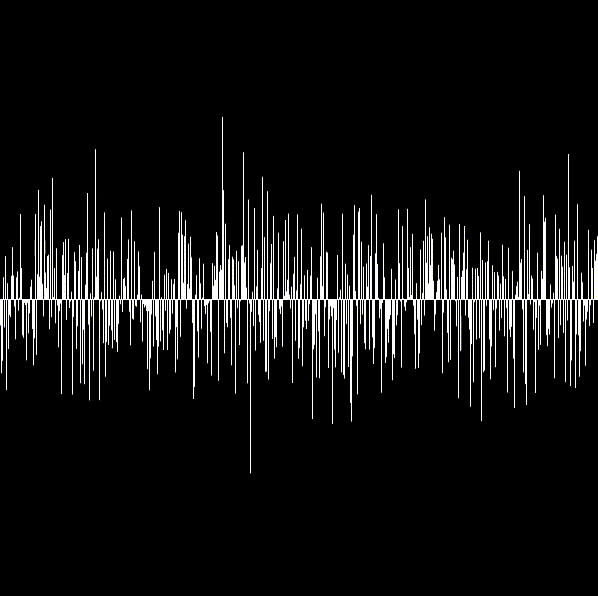
白い線が中心の線から上下に伸びているように見えます。
lineの第四引数がその上下に伸びる距離になるのですが、ここにrandomGaussian(300, 50)の返り値が入ります。
引数は中央値はcanvasの真ん中が来るように300を置いていて、標準偏差は50を渡しています。
平均に対して標準偏差を少なめに設定したため、300から離れた数値が変える可能性は低くなります。
そのため中心のラインは真っ白、離れるにつれて隙間が目立つように描画されます。