クリエイティブコーディングのためにsin, cosを学ぶ

この記事は Qiita p5js アドベントカレンダー15日目の記事です。

これはなに

私はp5.jsを学んでいますが、それなりのものを表現するにはある程度の数学的な知識が必要です。
これはコードベースのものだけではなく、TouchDesignerやmaxなどビジュアルベースのプログラミングにおいても同様だと思います。

特に座標を扱う上でsin, cos, tanの知識は不可欠なものと感じたため、コーディングのために三角関数について学び直し、それをまとめました。
今回は3つの方法でこれらの関数についてまとめていきます。

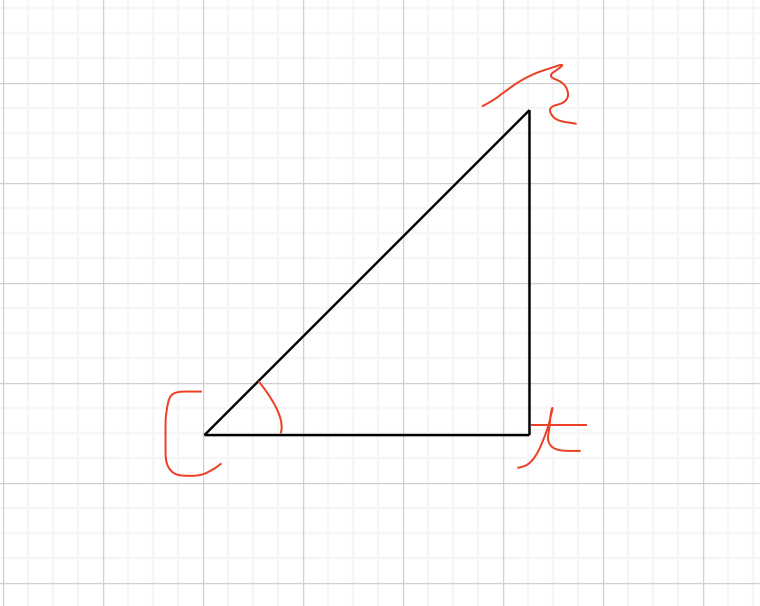
直角三角形で

書いてて懐かしくなりました。これです。

そしてこの式が成り立つことがここで伝えたい全てです。
（θは角度の部分）

sinθ = 高さ / 斜辺
cosθ = 横 / 斜辺

ただこれだけではコーディングとイメージを紐づけるのが難しいと思うので次にいきましょう。
　

円で

上記のことを円グラフで考えてみます。
半径1の円に原点からθだけ傾いた直線を引きます。
ここで求めたくなるのはこの直線と円が交わる頂点Aの座標です。

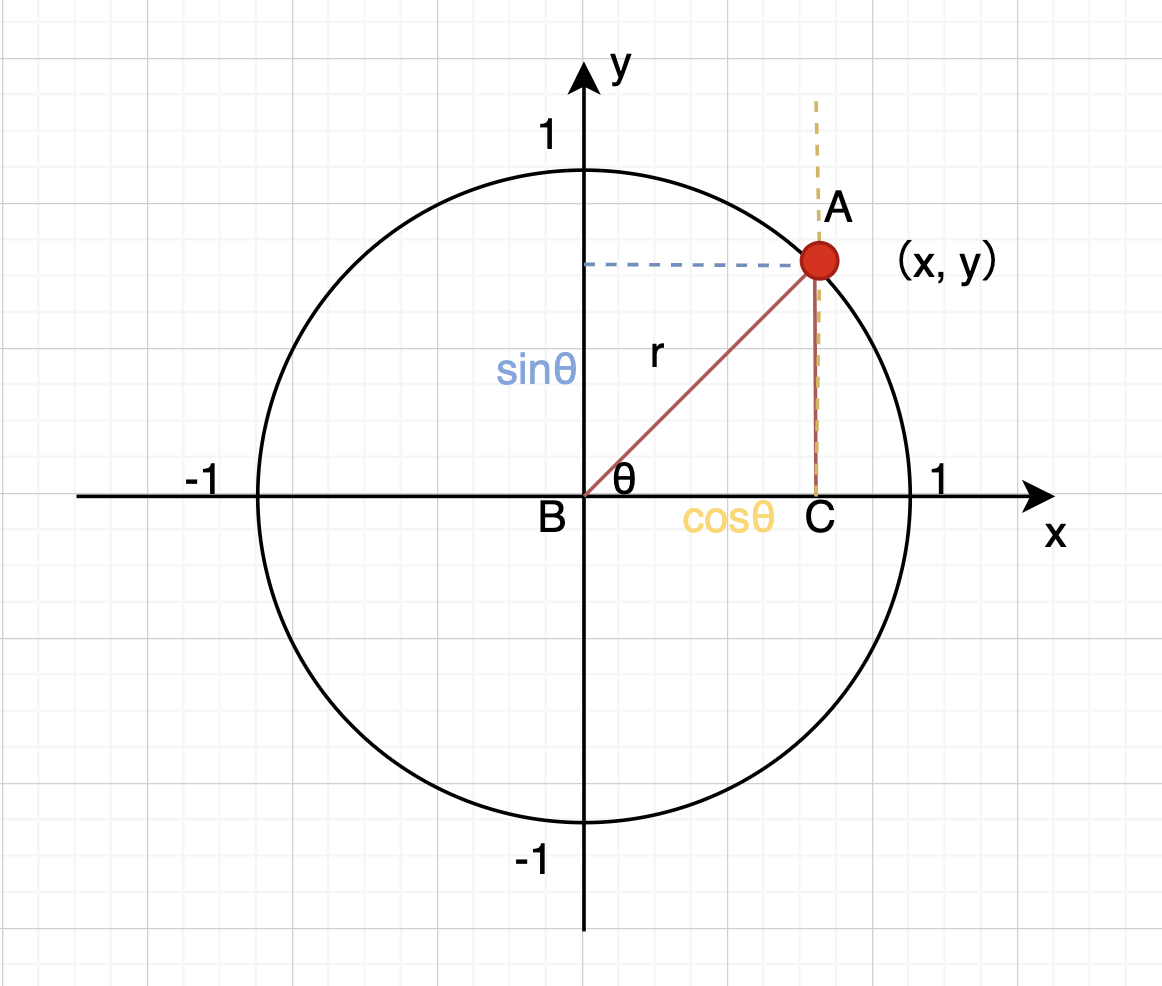
すると直角三角形が浮かび上がり、三角関数を適用することが可能に。
先ほど記載した公式から次のことが証明されます。

sinθ = 高さ / 斜辺より、sinθ = y
cosθ = 横 / 斜辺より、cosθ = x

よってAの座標は(cosθ, sinθ)であることが分かりました。
つまりsin関数とcos関数にθとなる値を渡すだけで簡単に座標を求めることができるのです。

試しに次のようなコードを書いてみました。
sin()、cos()で出した座標にpoint()を置き、半径50の円を描いています。

function setup() {
  createCanvas(600, 600);	
}

// 半径
let r = 50

function draw() {
  let angle = 0
  const inc = TWO_PI / 25
  background(200);
  
  for(let val = 0; val < 25; val++ ) {
    push()
    translate(width / 2, height / 2)
    strokeWeight(10);
    point(cos(angle) * r, sin(angle) * r)
    angle = angle + inc
    pop()
  }
}

グラフで

では今度は円ではなくグラフでみてみましょう。

の前にまず、度数の表現のことだけ記載しておきます。
度数の表現はラジアンと度の２種類があります。
ラジアンは聞き慣れないですが、「半径と等しい長さの弧に対する中心角の大きさ」を１としたものです。
もう一方の度はおなじみかと思います。

では180度をラジアンに変換するとどうなるでしょうか・・・
そう、（私にとっては）懐かしの円周率（π）です。

180度 = 3.141592653589793 ラジアン

p5にはあらかじめ定数PIとTWO_PIが用意されており、以下のような値が入っています。

PI => 3.14159265358979323846（180度）
TWO_PI => 6.28318530717958647693（360度）

---

はい！それではグラフについてまとめていきます。
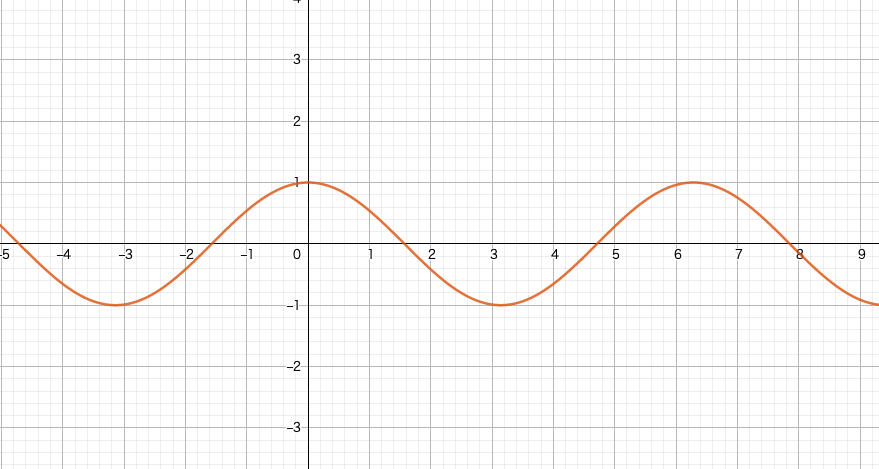
まずsin。次の図はy = sinθの図です。

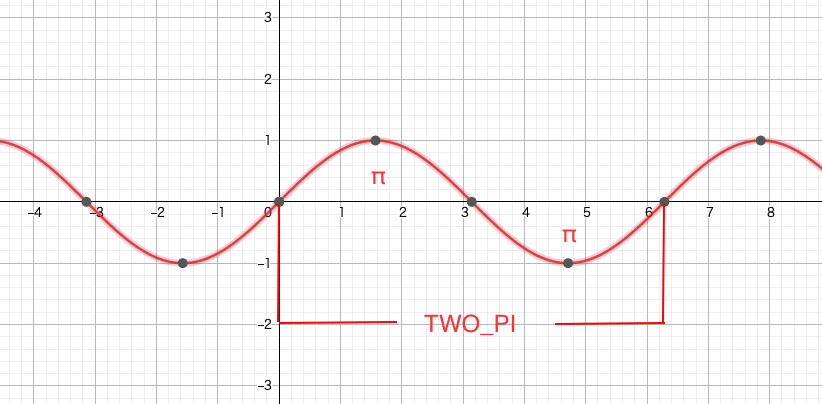
特徴は原点からスタートし、周期が2πであることです。
このsinの周期については過去に書いた記事、p5.jsの関数まとめ part.10 sin()を見ていただくとよりイメージが持てるかと思います。
とりあえず「こういう座標を通るグラフなんだ」と覚えてください。

次にy=cosθをグラフにしてみます。

こちらもsinと同様に周期は2πですが、スタートが(0, 0)ではなく(0, 1)です。

ではこれを利用して次のようにコードを書いてみます。

function setup() {
  createCanvas(600, 600);	
}

let angle = 0

function draw() {
  const inc = TWO_PI / 25
  translate(20, 20)
  background(0);
  for(let y = 0; y < 25; y++ ) {
    stroke(100)
    line(y * 20, 50, y * 20, 50 + sin(angle) * 40.0);
    stroke(150)
    line(y * 20, 50, y * 20, 50 + cos(angle) * 40.0);
    
    angle = angle + inc
  }
}

リファレンスにあるsin()のサンプルコードにcosの周期もプラスして描画してみました。
各線の座標がグラフと同じような位置にあることがわかります。

あとがき

いかがだったでしょうか。
あの日あの時学校で習った三角関数を、まさか今学び直すとは思いませんでした。

クリエイティブコーディングにおいてsin, cosは「こんなもの、こんな性質を持つ関数なんだ」ということをざっくりと把握しているだけでもだいぶ応用がきくと思います。
気が向いた時にtanについて勉強したことも書きます。

参考

弧度法とは？度数法との違いと表・求め方
p5.js reference | sin()
p5.js reference | angleMode()