逆関数について理解を広げていこう!
1. 関数ってなんだろう?
関数の知っている例をまずはあげてみましょう。
一次関数、二次関数、三角関数などいろいろありましたね。それぞれを式で表してみましょう。
1.1一次関数から振り返ってみよう
一次関数は次の形をしていましたね。
$$y=ax+b$$
これは$x$に何か値を入れると$y$が決まるという意味ですね。例えば次の例を考えてみましょう。
1.2具体的な例を考えてみよう。
$y=2x+1$では$x$をきめると$y$はどのようになるだろうか?
このグラフは傾き2の切片1の一次直線ですね。図で表すと以下のとおりです。
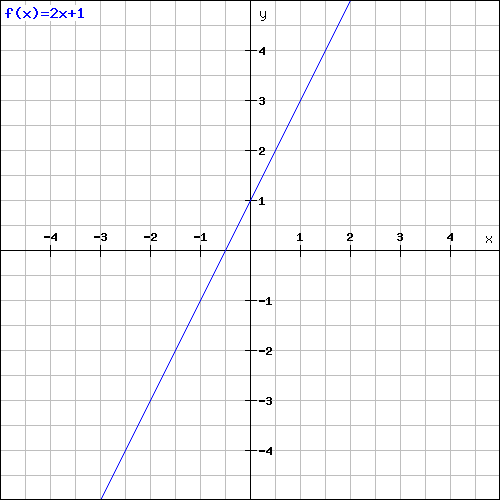
1.3 xの値を決めるとそれに対応したyの値が計算することにより簡単に決まる。
では$y$の値を決めた時はどうなるのでしょうか?
例えば、$y=1$となったとき、$x$の値はどうなるでしょうか?次の計算を行うことが一般的でしょう。
$$1=2x+1$$
1を移行して両辺を2で割ればいいわけですね。
そうして計算すると$x=0$であることがわかります。つまり、
$$y=1、x=0$$
グラフで見ると$(x,y)=(0,1)$を通過していることがわかりますね。
1.4 yから代入してもxの値を調べることができる。
では別の例を見てみましょう。$y=3$では$x$の値はどうなるでしょうか?
先ほどと同じように、yに3を代入してみましょう。
$$3=2x+1$$
$x$についてとくには、同じように1を移行して両辺を2で割りますね。
1.5yがあたえられたときにxをもとめるには1を移行して両辺を2で割りますすればよい。
でも毎回1を移行して両辺を2で割りますをするのがめんどうくさいですよね?どうすればいいでしょうか?毎回xから聞かれないでyから聞かれる場合は最初っからx=の形にしておけばいいですよね。
つまり、
$$x=\frac{y-1}{2}$$
の形にしておけばyが与えられた時にすぐにxの値を出すことができますね。
さらにグラフも書いておけばyを与えればすぐにビジュアル的にxの値をさがすことができますね。
ここで高校数学では左側のアルファベットをyと書くことが多いので以下のように直したほうが見やすいです。
$$y=\frac{x-1}{2}$$
このグラフを書いてみましょう。
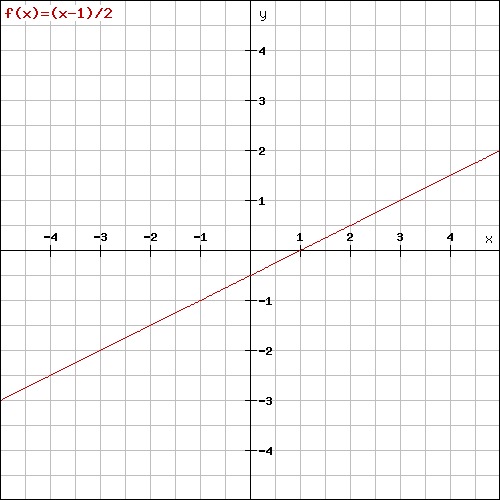
1.6 最初のグラフと比べてみよう。
$y=2x+1$と$y=\frac{x-1}{2}$の同じところに書いてみよう。どんなとくちょうがあるだろうか?
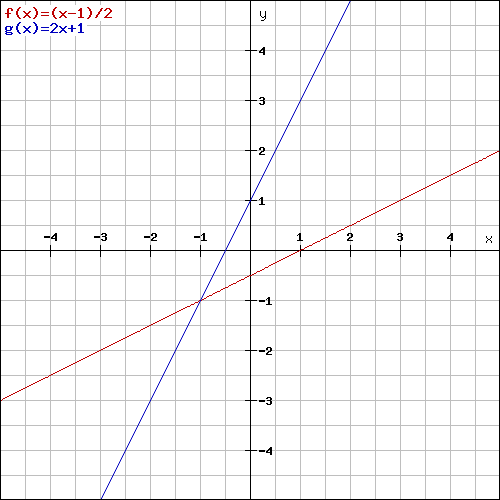
まとめ
◎関数の比較
| 元の関数 | $y$についての関数 |
|---|---|
| $y=2x+1$ | $y=\frac{x-1}{2}$ |
| ◎$y$についての関数に直す方法 | |
1を移行して両辺を2で割る |
|
| グラフにすることで、特徴をつかめるようになってきます。 | |
| 他の例も見てみましょう。すぐに特徴がつかめない場合は、いろいろな例を作ってグラフに書いていきましょう。 |
いくつかの例をあげてxについての関数と、yについての関数を整理してみよう。
例1 $y=3x+1$
例2 $y=x+4$
例3 $y=4x-1$
それぞれxについてのグラフとyについてのグラフをまとめていきましょう。