# 初めに
本記事はJDLAのE資格の認定プログラム「ラビット・チャレンジ」における深層学習day2のレポート記事です。この記事では以下の内容について、そのモデルの概念から確認し、数式・実装を含めてまとめていきます。
- 勾配消失問題
- 学習率最適化手法
- 過学習
- 畳み込みニューラルネットワークの概念
- 最新のCNN
#勾配消失問題
勾配消失問題は、ニューラルネットワークの設計において、勾配が消失することで学習が進まなくなる技術的な問題のことです。ニューラルネットワークによる学習を行う際、最もシンプルなモデルである単純パーセプトロンでは線形分離可能な問題しか学習できませんでした。よって非線形分離が必要となる問題では、パーセプトロンを多層化する必要があります。しかし多層化する場合には、予測値と実際の値の差分である誤差を最小化する、いわゆる最適化問題が複雑化します。多層ニューラルネットワークの最適化問題を解くためには、誤差逆伝播法(確率的勾配降下法など)を用います。この誤差を出力層から入力層に向かって逆向きに伝播しながら勾配を計算し、隠れ層の重みやバイアスが再計算するこの手法によって、容易にモデリングが可能となりました。
しかし、ここで問題が生じました。誤差逆伝播法が下位層に進んでいくにつれて勾配はどんどん緩やかになっていきます。そのため、勾配降下法による更新では、下位層のパラメータがほとんど変わらず、訓練が最適値に収束しなくなります。つまりニューラルネットワークは多層化するに従い、勾配が消えてしまったのです。これにより最適解が求められず、学習が進まなくなります。この勾配消失問題は局所最適化と並び、長年の多層ニューラルネットワークの問題でした。そこで以下に記述する解決法が提案されてきました。
##勾配消失問題の解決方法
###活性化関数
ReLU関数を使用することで、勾配消失問題の回避とスパース化に貢献することができます。ReLU関数は入力値が閾値(0)を超えている場合、入力値をそのまま出力する関数です。今最も使われている活性化関数です。
###重みの初期値設定
-
Xavier
重みの要素を、前層のノード数の平方根で除算した値を初期値とするアルゴリズムです。 Xavier初期値を設定する際の活性化関数は、ReLU関数、シグモイド関数、双曲線正接関数(tanh)があります。 -
He
重みの要素を、前層のノード数の平方根で除算した値に2‾√を掛けた値を初期値とするアルゴリズムです。 Heの初期値を設定する際の活性化関数は、ReLU関数があげられます。
###バッチ正規化
ミニバッチ単位で入力値のデータの偏りを抑制する手法です。活性化関数に値を渡す前後にバッチ正規化の処理を含む層を加えます。つまり、ミニバッチごとに正規化(標準化)することです。ここで言う正規化とは、ミニバッチデータの分布が平均が0で標準偏差が1になるようにすることです。ソフトマックス関数によりデータの総和が1になるようにする正規化とは全く別の意味です。
-> 学習の安定化や速度アップが期待できます。
##コード実装
MNISTのデータセットを使用して勾配消失問題について検討しました。
以下のコードは、活性化関数にシグモイド関数、初期値はガウス関数を元に生成した乱数を使用しています。
import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt
# mnistをロード
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = len(x_train)
print("データ読み込み完了")
# 重み初期値補正係数
wieght_init = 0.01
#入力層サイズ
input_layer_size = 784
#中間層サイズ
hidden_layer_1_size = 40
hidden_layer_2_size = 20
#出力層サイズ
output_layer_size = 10
# 繰り返し数
iters_num = 2000
# ミニバッチサイズ
batch_size = 100
# 学習率
learning_rate = 0.1
# 描写頻度
plot_interval=10
# 初期設定
def init_network():
network = {}
network['W1'] = wieght_init * np.random.randn(input_layer_size, hidden_layer_1_size)
network['W2'] = wieght_init * np.random.randn(hidden_layer_1_size, hidden_layer_2_size)
network['W3'] = wieght_init * np.random.randn(hidden_layer_2_size, output_layer_size)
network['b1'] = np.zeros(hidden_layer_1_size)
network['b2'] = np.zeros(hidden_layer_2_size)
network['b3'] = np.zeros(output_layer_size)
return network
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_f = functions.sigmoid
u1 = np.dot(x, W1) + b1
z1 = hidden_f(u1)
u2 = np.dot(z1, W2) + b2
z2 = hidden_f(u2)
u3 = np.dot(z2, W3) + b3
y = functions.softmax(u3)
return z1, z2, y
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
hidden_d_f = functions.d_sigmoid
last_d_f = functions.d_softmax_with_loss
# 出力層でのデルタ
delta3 = last_d_f(d, y)
# b3の勾配
grad['b3'] = np.sum(delta3, axis=0)
# W3の勾配
grad['W3'] = np.dot(z2.T, delta3)
# 2層でのデルタ
delta2 = np.dot(delta3, W3.T) * hidden_d_f(z2)
# b2の勾配
grad['b2'] = np.sum(delta2, axis=0)
# W2の勾配
grad['W2'] = np.dot(z1.T, delta2)
# 1層でのデルタ
delta1 = np.dot(delta2, W2.T) * hidden_d_f(z1)
# b1の勾配
grad['b1'] = np.sum(delta1, axis=0)
# W1の勾配
grad['W1'] = np.dot(x.T, delta1)
return grad
# パラメータの初期化
network = init_network()
accuracies_train = []
accuracies_test = []
# 正答率
def accuracy(x, d):
z1, z2, y = forward(network, x)
y = np.argmax(y, axis=1)
if d.ndim != 1 : d = np.argmax(d, axis=1)
accuracy = np.sum(y == d) / float(x.shape[0])
return accuracy
for i in range(iters_num):
# ランダムにバッチを取得
batch_mask = np.random.choice(train_size, batch_size)
# ミニバッチに対応する教師訓練画像データを取得
x_batch = x_train[batch_mask]
# ミニバッチに対応する訓練正解ラベルデータを取得する
d_batch = d_train[batch_mask]
z1, z2, y = forward(network, x_batch)
grad = backward(x_batch, d_batch, z1, z2, y)
if (i+1)%plot_interval==0:
accr_test = accuracy(x_test, d_test)
accuracies_test.append(accr_test)
accr_train = accuracy(x_batch, d_batch)
accuracies_train.append(accr_train)
print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
print(' : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
# パラメータに勾配適用
for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
network[key] -= learning_rate * grad[key]
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test, label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()
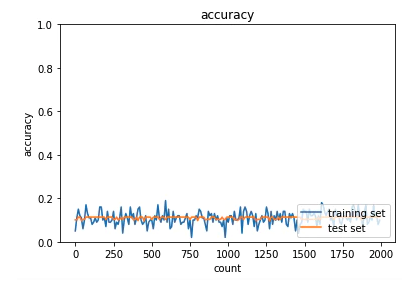
学習回数を重ねてもaccuracyが向上しないことから、勾配消失による学習問題であることが推測できます。
検討:初期値固定で活性化関数をReLU
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
########### 変更箇所 ###########
hidden_f = functions.relu
#################################
# 誤差逆伝播
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
########### 変更箇所 ###########
hidden_d_f = functions.d_relu
#################################
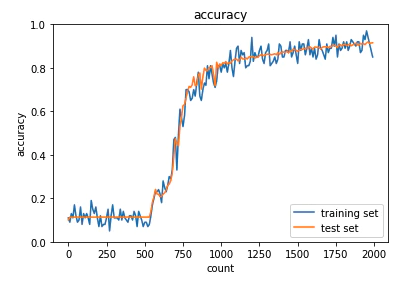
活性化関数をReLUに変更したことで勾配消失問題が改善されました。
初期値をHe、活性化関数をReLUとして学習
def init_network():
network = {}
########### 変更箇所 ##############
# Heの初期値
network['W1'] = np.random.randn(input_layer_size, hidden_layer_1_size) / np.sqrt(input_layer_size) * np.sqrt(2)
network['W2'] = np.random.randn(hidden_layer_1_size, hidden_layer_2_size) / np.sqrt(hidden_layer_1_size) * np.sqrt(2)
network['W3'] = np.random.randn(hidden_layer_2_size, output_layer_size) / np.sqrt(hidden_layer_2_size) * np.sqrt(2)
#################################
# 順伝播
def forward(network, x):
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
########### 変更箇所 ##############
hidden_f = functions.relu
#################################
def backward(x, d, z1, z2, y):
grad = {}
W1, W2, W3 = network['W1'], network['W2'], network['W3']
b1, b2, b3 = network['b1'], network['b2'], network['b3']
########### 変更箇所 ##############
hidden_d_f = functions.d_relu
#################################
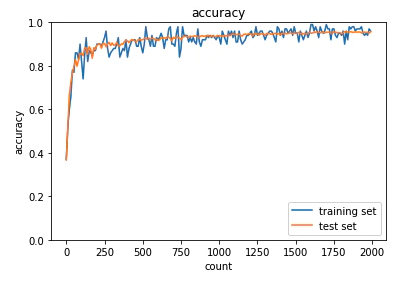
学習の初期段階で正解率が80%を超え、最終的な正解率も96%となり、training data と test dataの乖離も見られないため、好ましい結果と言えます。
###確認テスト1
連鎖率の原理を使い、
$$
\begin{aligned}
&z=t^{2} \
&t=x+y
\end{aligned}
$$
の時、dz/dxを求めよ。
$$
\frac{d z}{d x}=\frac{d z}{d t} \frac{d t}{d x}=2 t \times 1=2(x+y)
$$
###確認テスト2
シグモイド関数を微分した時、入力値が0の時に最大値をとる。その値を答えよ。
シグモイド関数の微分の式
$$
f(u)=(1-\operatorname{sigmoid}(u)) \cdot \operatorname{sigmoid}(u)
$$
シグモイド関数の入力が0の時、出力は0.5となるため「0.5×0.5=0.25」となります。
###確認テスト3
重みの初期値に0を設定すると、どのような問題が発生するか。
-> 全てのパラメータが同じ値で伝播し、値の最適化が出来ないため学習が進みません。
###確認テスト4
一般的に考えられるバッチ正規化の効果を2点挙げよ。
- 勾配消失問題の抑制
- 計算の効率化
#学習率最適化手法
以下の内容を確認した後、実装とモデルの検討を行なっています。
- モメンタム
- AdaGrad
- RMSProp
- Adam
##モメンタム
勾配降下法では、誤差をパラメータで微分したものと学習率の積を減算していました。 モメンタムでは、誤差をパラメータで微分したものと学習率の積を減算した後、現在の重みに前回の重みを減算した値と慣性の積を加算します。
\begin{gathered}
V_{t}=\mu V_{t-1}-\epsilon \nabla E \\
w^{t+1}=w^{t}+V_{t}
\end{gathered}
メリット
-> 局所的最適解にはならず、大域的最適解となります。また、谷間から最適解までたどり着くのが早いことも特徴です。
class Momentum:
def __init__(self, learning_rate=0.01, momentum=0.9):
self.learning_rate = learning_rate
self.momentum = momentum
self.v = None
def update(self, params, grad):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key] - self.learning_rate * grad[key]
params[key] += self.v[key]
##AdaGrad
誤差をパラメータで微分したものと再定義した学習率の積を減算します。
\begin{gathered}
h_{0}=\theta \\
h_{t}=h_{t-1}+(\nabla E)^{2} \\
w^{t+1}=w^{t}-\epsilon \frac{1}{\sqrt{h_{t}}+\theta} \nabla E
\end{gathered}
利点
勾配の緩やかな斜面に対して最適解に近づけることができます。
課題
学習率が徐々に小さくなるので鞍点問題を引き起こすことがあります。
class AdaGrad:
def __init__(self, learning_rate=0.01):
self.learning_rate = learning_rate
self.h = None
def update(self, params, grad):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grad[key] * grad[key]
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key])
##RMSProp
Adagradの改良版
\begin{aligned}
&h_{t}=\alpha h_{t-1}+(1-\alpha)(\nabla E)^{2} \\
&w^{t+1}=w^{t}-\epsilon \frac{1}{\sqrt{h_{t}}+\theta} \nabla E
\end{aligned}
メリット
- 局所最適解にはならずに大域的最適解となります。
- ハイパーパラメータの調整が必要な場合が多いです。
class RMSprop:
def __init__(self, learning_rate=0.01, decay_rate = 0.99):
self.learning_rate = learning_rate
self.decay_rate = decay_rate
self.h = None
def update(self, params, grad):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grad[key] * grad[key]
params[key] -= self.learning_rate * grad[key] / (np.sqrt(self.h[key]) + 1e-7)
##Adam
これまでのオプティマイザーの良い点を全て合わせた最適化アルゴリズムです。
- モメンタムの過去の勾配の指数関数的減衰平均
- RMSPropの過去の勾配の2乗の指数関数的減衰平均
class Adam:
def __init__(self, learning_rate=0.001, beta1=0.9, beta2=0.999):
self.learning_rate = learning_rate
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grad):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.learning_rate * np.sqrt(1.0 - self.beta2 ** self.iter) / (1.0 - self.beta1 ** self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) * (grad[key] - self.m[key])
self.v[key] += (1 - self.beta2) * (grad[key] ** 2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)
##optimizer実装
optimizerの全実装コードと検討結果
###確認テスト1
モメンタム、AdaGrad、RMSpropの特徴をそれぞれ簡潔に説明せよ。
- モメンタム:勾配の移動平均を出して振動を抑える(過去の勾配たちを考慮することで急な変化を抑える)。
- AdaGrad:次元ごとに学習率を変化させるようにしたもの。
- RMSprop:AdaGradの改良版であり、一度学習率が0に近づくとほとんど変化しなくなるAdaGradの問題を改良したもの。
#過学習
過学習とは、学習データに過剰に適合することで、学習データでは正解率が高いのに正解データでは正解率が低くなってしまうことです。つまり、学習データだけに最適化されてしまって汎用性がない状態に陥るため実際の運用では役に立ちません。なので、未知データを処理した時に、高い精度を発揮できなくては意味がないということです。
過学習を抑制する手法
過学習を抑制するには、早期終了というアイデアがあります。学習データを処理しながら、随時多くのパラメーターを更新していくわけですが、ある時点から学習データだけに適合するようになっていくので、そのタイミングで学習を終了してしまうということです。単純で、理屈としてはよく分かります。ただ、その時点で目標とする精度に達していれば良いですが、そうでない場合、学習を止めるだけでは、高精度なモデルが得られるわけではありません。
そこで、以下に3つの過学習を抑制する手法をまとめました。
-
学習のデータ数増加
学習データの数が多ければ多いほど、学習データのバリエーションが増えていき、未知データに近づきます。そのため、データ分析を始めようとする場合、まずは今の時点でインプットデータがどのくらい収集、準備できているのかを確認することが重要です。そして、学習データをもっと収集できないか、どうしても出来ない場合には、手作りでの加工や機械的にクローンデータを水増しできないかに取り組むことで改善が見込めます。 -
正則化
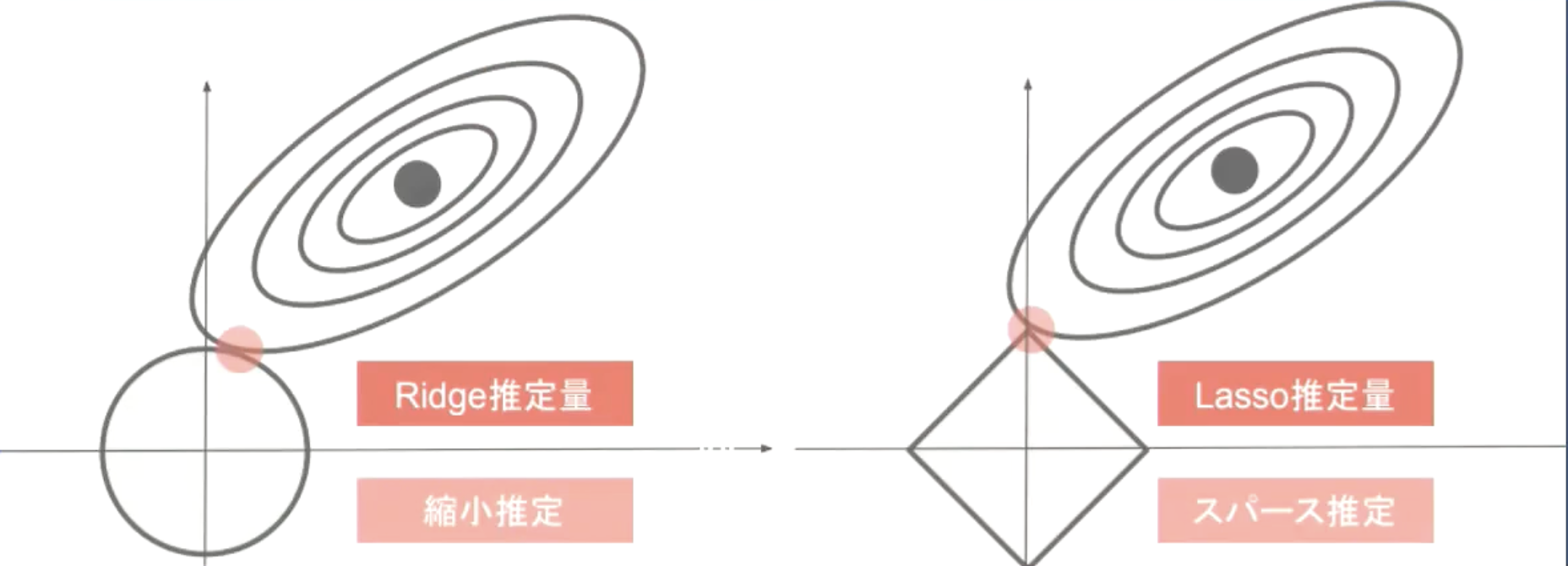
ある意味では複雑なモデルを単純なモデルへ変化させていく数学的な手法と言えると思います。つまり、不要なパラメータの影響を小さくすることで複雑なモデルを単純なモデルに変えていきながら、過学習を防ぐことです。過学習を防ぐための正則化には、主に「L1正則化」と「L2正則化」という2種類の方法が用いられます。L2正則化がモデルの過学習を避けるために用いられる一方、L1正則化は不要な説明変数をそぎ落とす次元圧縮のために用いられます。
L1正則化(Lasso回帰)
L1正則化は、あらかじめ選択したデータの重みを0にすることによって、不要なデータを削除するための方法です。
L2正則化(Ridge回帰)
L2正則化は、データの大きさに合わせて0に近づけていくという手法で、滑らかなモデルを構築できることが特徴です。
-
モデルの単純化・ドロップアウト
ネットワーク自由度を強制的に小さくして過学習を避ける方法としてドロップアウトがあります。多層ネットワークの各層のユニットを確率的に選別して、選別したもの以外を無効化することで「自由度の小さい仮のネットワーク」を構築できます。その上で学習させることでモデルを簡素化したような効果が得られます。
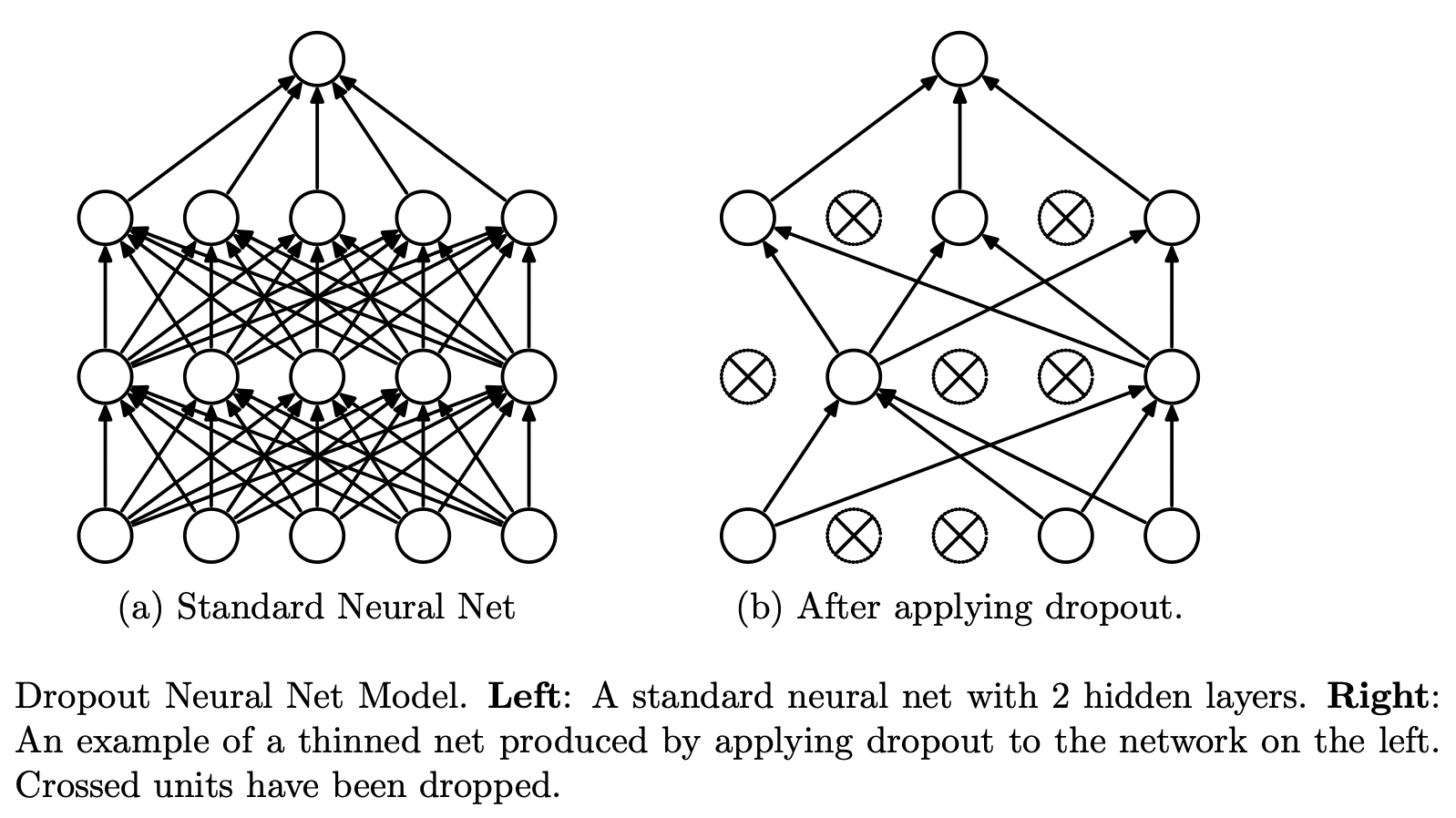
ドロップアウト
過学習を抑制する方法として、Dropoutが提案されています。Dropoutは特定のレイヤーの出力を学習時にランダムで0に落とすことで、一部のデータが欠損していても正しく認識ができるようにします。これにより、画像の一部の局所特徴が過剰に評価されてしまうのを防ぎ、モデルのロバストさを向上させることができます。
引用:Dropout: A Simple Way to Prevent Neural Networks from Overfitting
##実装コード
下記の内容の実装と検討
- overfiting
- L2
- L1
- Dropout
- Dropout + L1
###確認テスト1
下図について、L1正則化を表しているグラフはどちらか答えよ。
ラビットチャレンジ講義資料より引用
-> 右のLasso推定量がL1正則化を表している。
#畳み込みニューラルネットワークの概念
畳み込みネットワークは主に画像認識で用いられ、その圧倒的な精度ゆえにディープラーニングが注目される1つの要因を作り出した手法です。畳み込みニューラルネットワークとは、画像データを入力として、高い認識性能を達成できるモデルです。通常のニューラルネットワークと同様に、誤差逆伝播法を学習に使います。下記のような、私たち人間が持っている視覚野の神経細胞の働きを模倣してみよう、という発想から生まれました。
- 単純型細胞(S細胞):画像の濃淡パターン(特徴)を検出する。
- 複雑型細胞(C細胞):空間的な位置のずれを吸収し、同一の特徴であるとみなす。
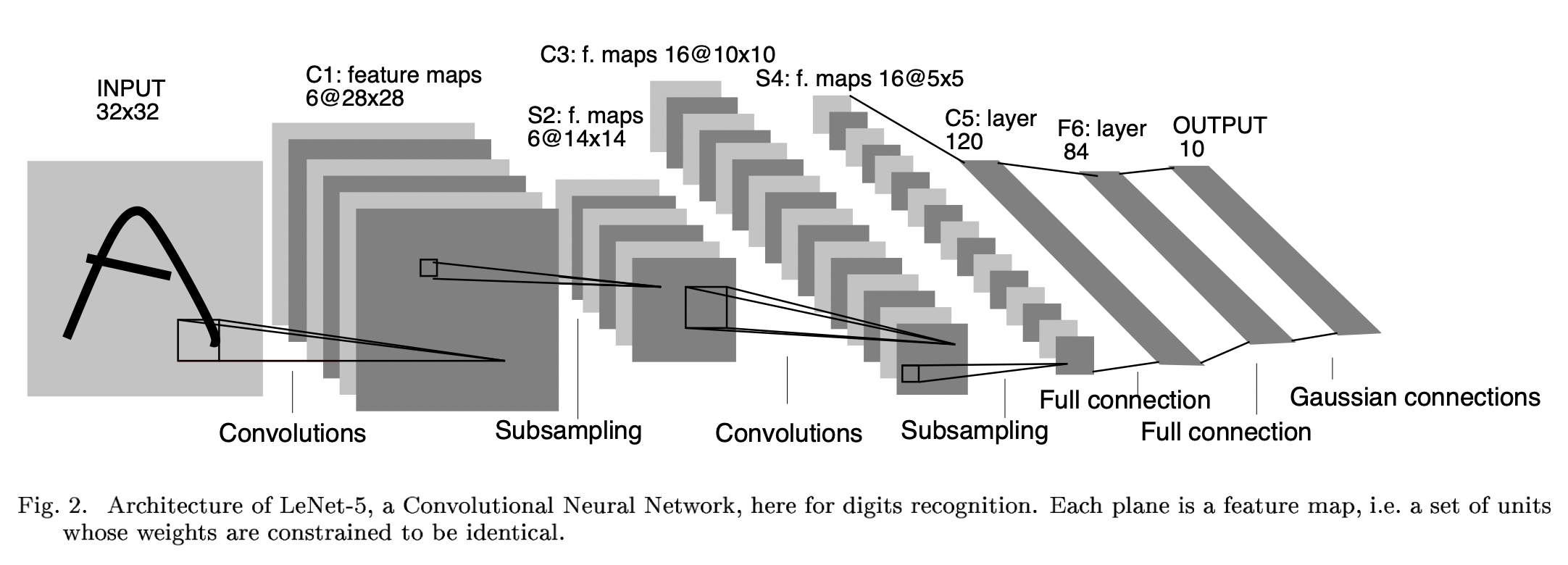
このS細胞、C細胞の働きを最初に組み込んだモデルがネオコグ二トロンです。ネオコグ二トロンは、従来のニューラルネットワークのように、S細胞層とC細胞層を交互に複数組み合わせた構造になっています。また、LeNetという畳み込みニューラルネットワークのモデルもあります。LeNetは、畳み込み層とプーリング層の2種類を複数組み合わせた構造になっています。ネオコグ二トロンのS細胞層がLeNetにおける畳み込み層、C細胞層がプーリング層になります。
引用:Yan LeCun(1998) Gardient-Based Learning Applied To Document Recognition
##畳み込み層
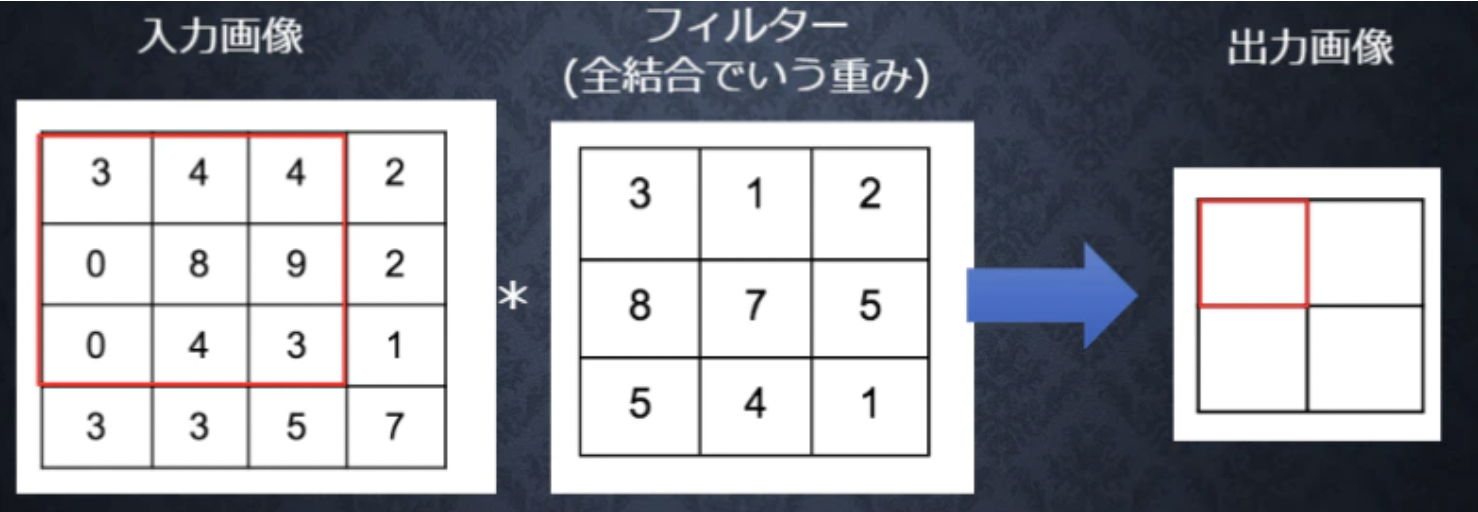
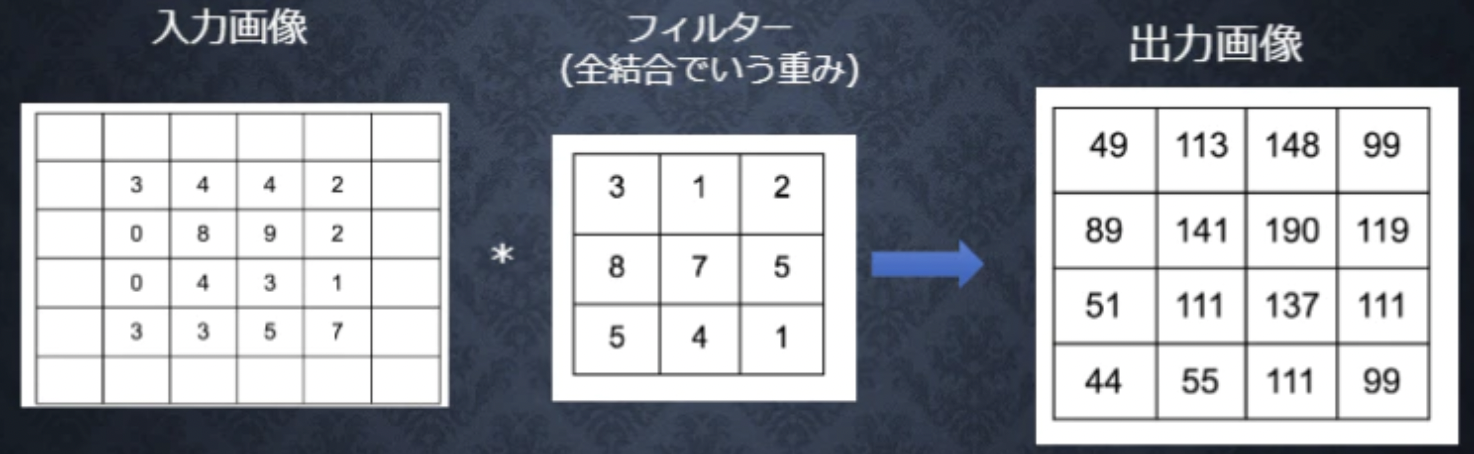
前述の通り、畳み込み層は単純型細胞をモデルに考えられたもので、単純型細胞と同様、特定の形状に反応するように構成されています。この特定の形状はフィルタと呼ばれ、データによる学習時に自動調整されます。畳み込み層では、画像の場合、縦、横、チャンネルの3次元のデータをそのまま学習し、次に伝えることができます。なので、畳み込み層は3次元の空間情報も学習できるような層のことを言います。フィルタを画像の左上から順番に重ね、画像とフィルタの値を掛け合わせます。掛け合わせた数値の総和をもとめ、特徴マップという新たな2次元データを取得します。
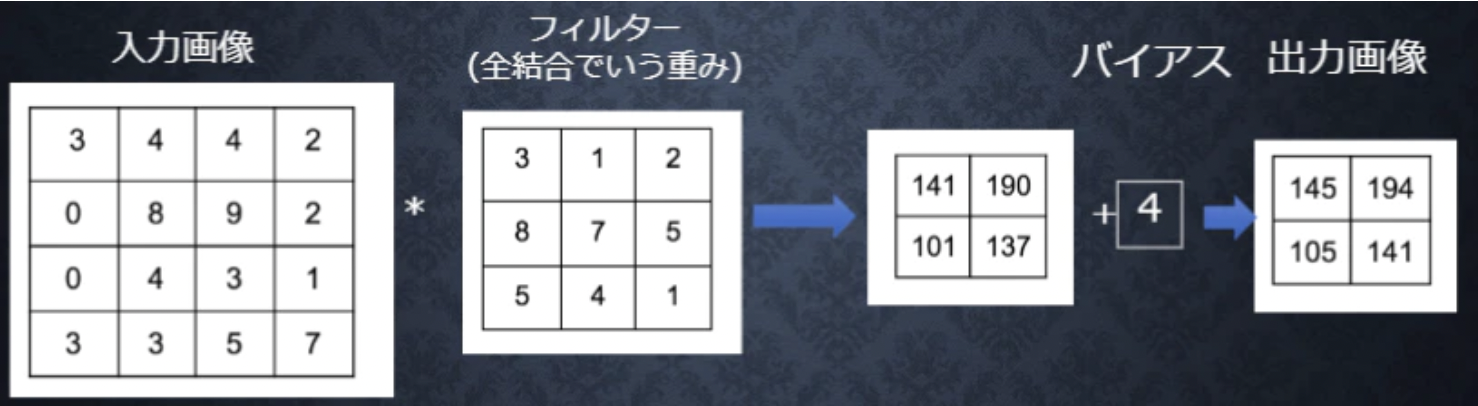
###バイアス
バイアスはフィルター適用後のデータに加算されます。バイアスの値は1つだけであり、同じ値がフィルター適用後のすべての要素に加算されます。
###パディング
出力サイズを調整するため、畳み込み層の処理を行う前に、入力データの周囲に例えば0などの固定のデータを埋めることです。
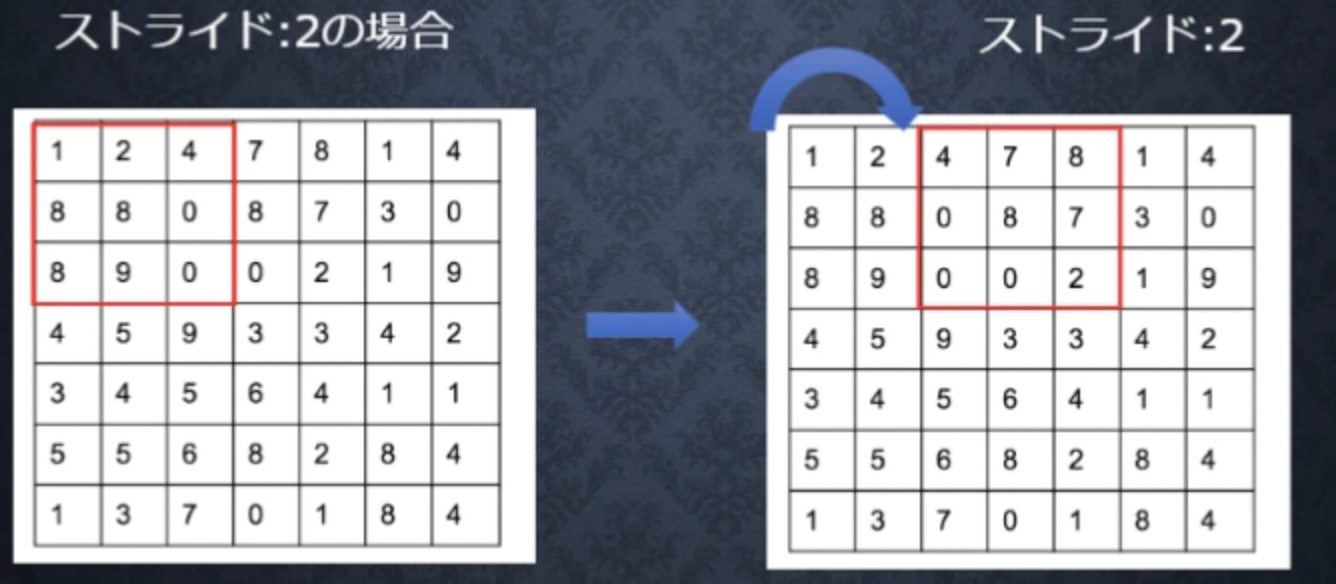
###ストライド
フィルターを適用する間隔のことです。ストライドを大きくすると出力サイズは小さくなります。
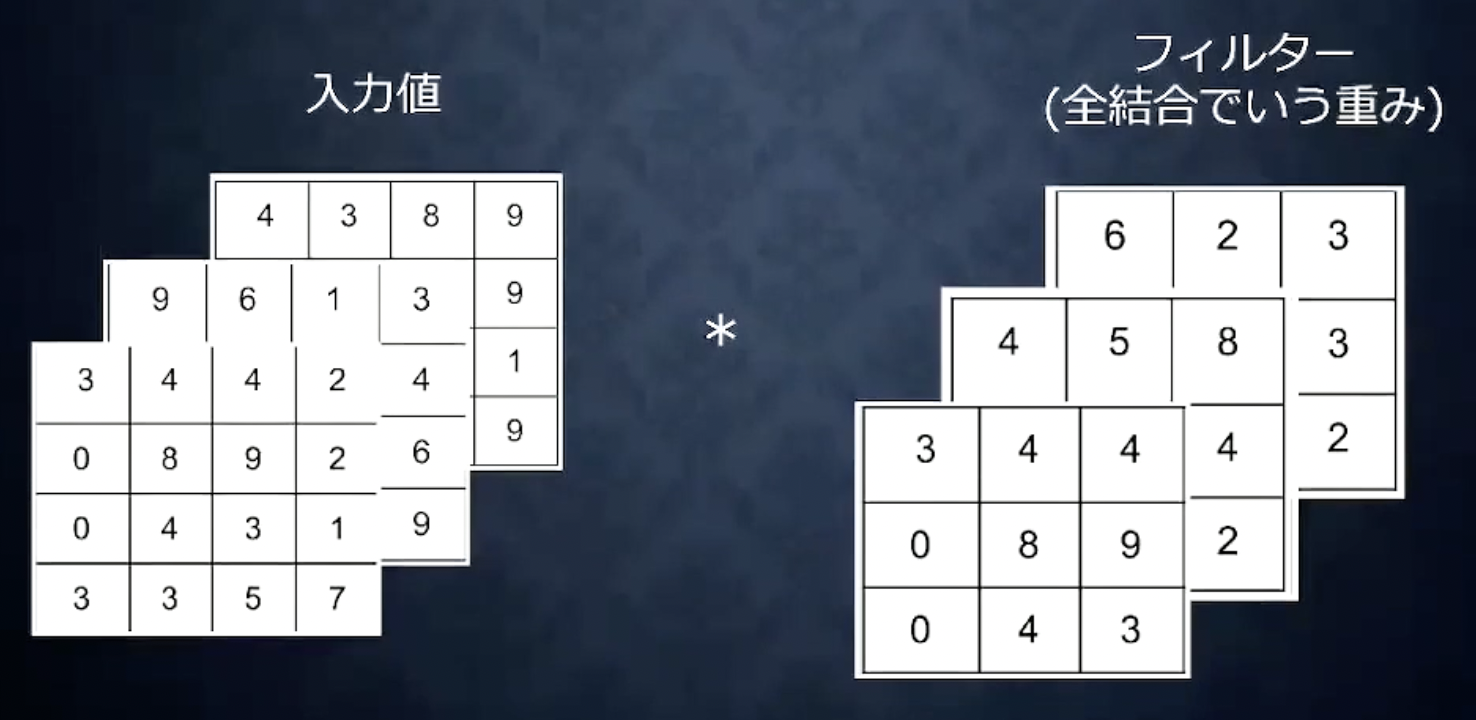
###チャンネル
これまでの例では、入力データはW×Hの2次元画像でしたが、3次元でも畳み込み演算は可能です。チャンネルを増やす例としては、RGBのカラー画像を学習するときが考えられます。R、G、Bのそれぞれを各チャンネルとしCNNへの入力として扱います。
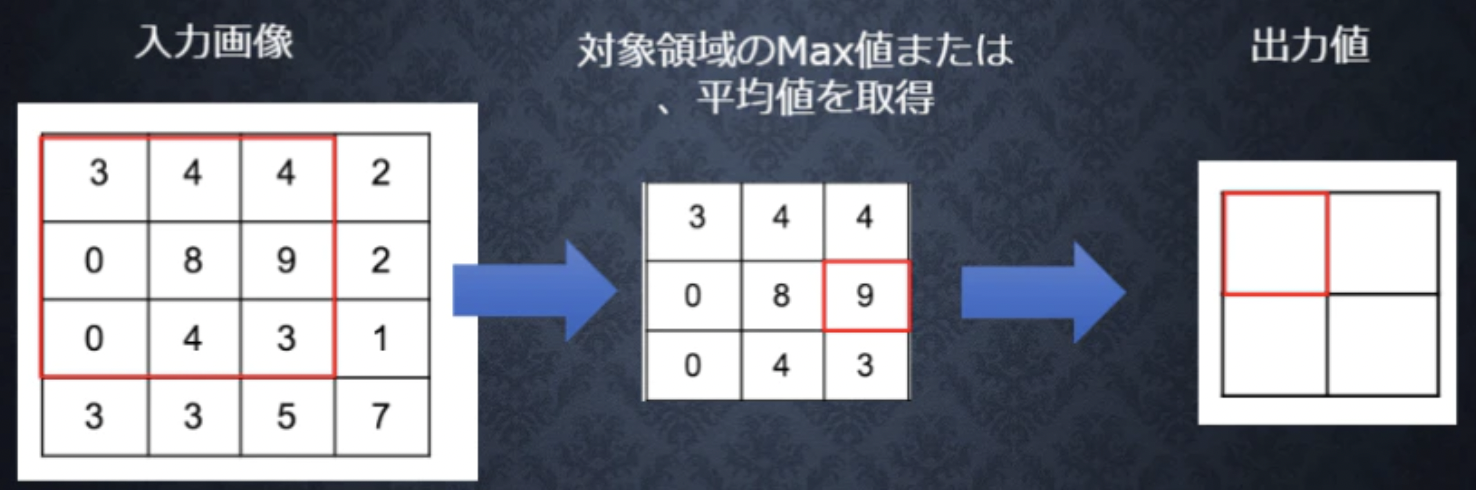
##プーリング層
プーリング層は、複雑型細胞をモデル化したもので、入力画像におけるフィルタ形状の位置ずれを吸収するように機能します。その仕組みは、畳み込み層と比較するとかなり単純です。プーリング層の個々のニューロンは、畳み込み層の一定領域のニューロンと結合します。ただし、この畳み込み層の領域同士は重複せず、1つの畳み込み層ニューロンは、ただ1つのプーリング層ニューロンのみと結合します。プーリングは、ダウンサンプリングやサブサンプリングとも呼ばれ、特徴マップのサイズを決められた演算を行って小さくしていきます。
##全結合層
全結合層は、通常のニューラルネットワークにおける隠れ層と出力層に相当します。全結合層では、これまで出力してきた画像が「5という文字」「ネコ」「りんご」などと判別できるように、1次元にします。
##実装コード
simple convolution networkの実装
###確認テスト1
サイズ6×6の入力画像を、サイズ2×2のフィルタで畳み込んだ時の出力画像のサイズを答えよ。なお、ストライドとパディングは1とする。
求める出力幅をOW、出力高をOHとすると、以下のように求められます。
\begin{gathered}
O W=\frac{W+2 p-F w}{s}+1=\frac{6+2-2}{1}+1=7 \\
O H=\frac{H+2 p-F h}{s}+1=\frac{6+2-2}{1}+1=7
\end{gathered}
#最新のCNN
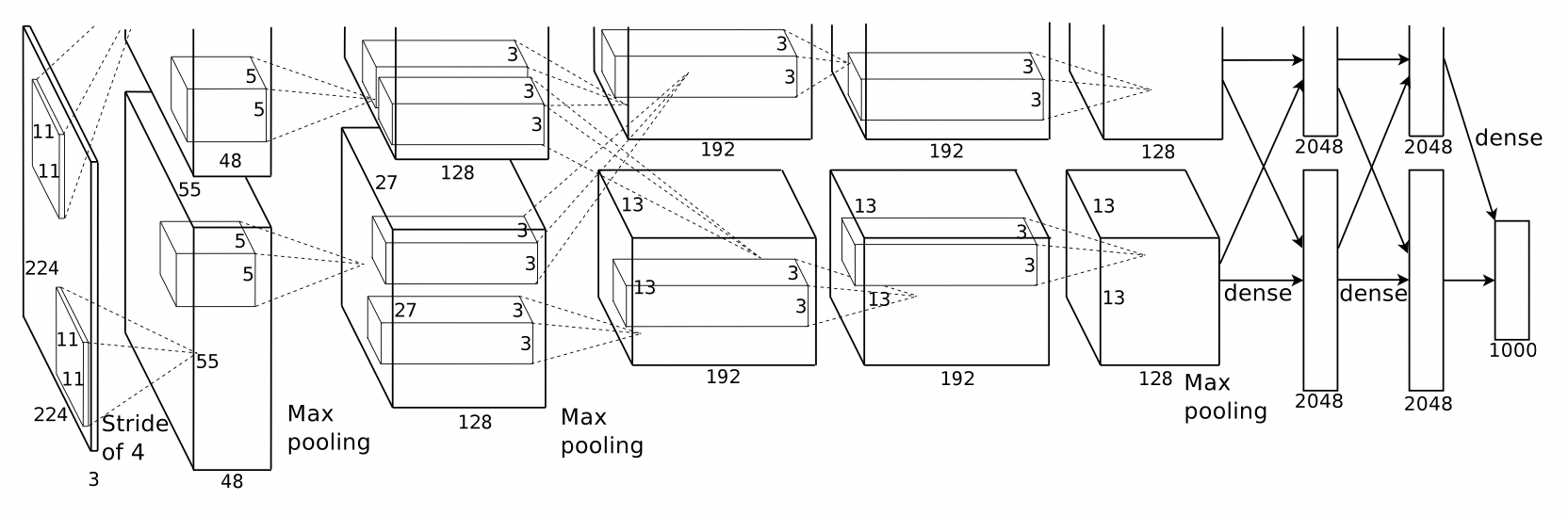
##AlexNet
最新のCNNを理解するために、最も理解しやすいAlexNetについてまとめます。
AlexNetはHinton教授らのチームによって発表された物体認識のためのアーキテクチャです。AlexNetは物体認識のために、初めて深層学習の概念および畳み込みニューラルネットワークの概念を取り入れたアーキテクチャで、2012年の画像認識コンペILSVRCにおいて最も高い精度を出しました。
モデル構造
第1層: 入力224×224×3の画像について11×11×3で畳み込み演算
-> 96個のkernelに変換
第2層: 55×55の画像を5×5のフィルターでmax pooling
-> 256個のkernelに変換
第3層: 27×27の画像を3×3のフィルターでmax pooling
-> 384個のkernelに変換
第4層: 3×3でパディング処理(画像のサイズが変わらないように処理)
-> 384個のkernelに変換
第5層: 13×13×256の数字をFratten(ベクトル化:43,264)
-> 2つの全結合層: 4096個のニューロン
(過学習を防ぐ施策:ドロップアウトを採用)
出力層: 最終的に1000個の数字の集まりまで縮小する
画像引用:ImageNet Classification with Deep Convolutional Neural Networks
#参考文献