言語処理100本ノック 2015の挑戦記録です。環境はUbuntu 16.04 LTS + Python 3.5.2 :: Anaconda 4.1.1 (64-bit)です。過去のノックの一覧はこちらからどうぞ。
第8章: 機械学習
本章では,Bo Pang氏とLillian Lee氏が公開しているMovie Review Dataのsentence polarity dataset v1.0を用い,文を肯定的(ポジティブ)もしくは否定的(ネガティブ)に分類するタスク(極性分析)に取り組む.
79. 適合率-再現率グラフの描画
ロジスティック回帰モデルの分類の閾値を変化させることで,適合率-再現率グラフを描画せよ.
出来上がったコード:
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
fname_result = 'result.txt'
fname_work = 'work.txt'
def score(fname):
'''結果ファイルからスコア算出
結果ファイルを読み込んで、正解率、適合率、再現率、F1スコアを返す
戻り値:
正解率,適合率,再現率,F1スコア
'''
# 結果を読み込んで集計
TP = 0 # True-Positive 予想が+1、正解も+1
FP = 0 # False-Positive 予想が+1、正解は-1
FN = 0 # False-Negative 予想が-1、正解は+1
TN = 0 # True-Negative 予想が-1、正解も-1
with open(fname) as data_file:
for line in data_file:
cols = line.split('\t')
if len(cols) < 3:
continue
if cols[0] == '+1': # 正解
if cols[1] == '+1': # 予想
TP += 1
else:
FN += 1
else:
if cols[1] == '+1':
FP += 1
else:
TN += 1
# 算出
accuracy = (TP + TN) / (TP + FP + FN + TN) # 正解率
precision = TP / (TP + FP) # 適合率
recall = TP / (TP + FN) # 再現率
f1 = (2 * recall * precision) / (recall + precision) # F1スコア
return accuracy, precision, recall, f1
# 結果読み込み、予測確率は元の値(仮説関数hypothesis()の値)に戻す
results = []
with open(fname_result) as data_file:
for line in data_file:
cols = line.split('\t')
if len(cols) < 3:
continue
# 正解ラベル
label = cols[0]
# 識別関数predict()の値
if cols[1] == '-1':
predict = 1.0 - float(cols[2]) # 確率を戻す
else:
predict = float(cols[2])
results.append((label, predict))
# 閾値を変えながらスコア算出、グラフ描画用の配列へセット
thresholds = []
accuracys = []
precisions = []
recalls = []
f1s = []
for threshold in np.arange(0.02, 1.0, 0.02):
# score()を使うため、一時ファイルに結果保存
with open(fname_work, 'w') as file_out:
for label, predict in results:
if predict > threshold:
file_out.write('{}\t{}\t{}\n'.format(label, '+1', predict))
else:
file_out.write('{}\t{}\t{}\n'.format(label, '-1', 1 - predict))
# スコア算出
accuracy, precision, recall, f1 = score(fname_work)
# 結果追加
thresholds.append(threshold)
accuracys.append(accuracy)
precisions.append(precision)
recalls.append(recall)
f1s.append(f1)
# グラフで使うフォント情報(デフォルトのままでは日本語が表示できない)
fp = FontProperties(
fname='/usr/share/fonts/truetype/takao-gothic/TakaoGothic.ttf'
)
# 折線グラフの値の設定
plt.plot(thresholds, accuracys, color='green', linestyle='--', label='正解率')
plt.plot(thresholds, precisions, color='red', linewidth=3, label='適合率')
plt.plot(thresholds, recalls, color='blue', linewidth=3, label='再現率')
plt.plot(thresholds, f1s, color='magenta', linestyle='--', label='F1スコア')
# 軸の値の範囲の調整
plt.xlim(
xmin=0, xmax=1.0
)
plt.ylim(
ymin=0, ymax=1.0
)
# グラフのタイトル、ラベル指定
plt.title(
'79. 適合率-再現率グラフの描画', # タイトル
fontproperties=fp # 使うフォント情報
)
plt.xlabel(
'ロジスティック回帰モデルの分類の閾値', # x軸ラベル
fontproperties=fp # 使うフォント情報
)
plt.ylabel(
'精度', # y軸ラベル
fontproperties=fp # 使うフォント情報
)
# グリッドを表示
plt.grid(axis='both')
# 凡例表示
plt.legend(loc='lower left', prop=fp)
# 表示
plt.show()
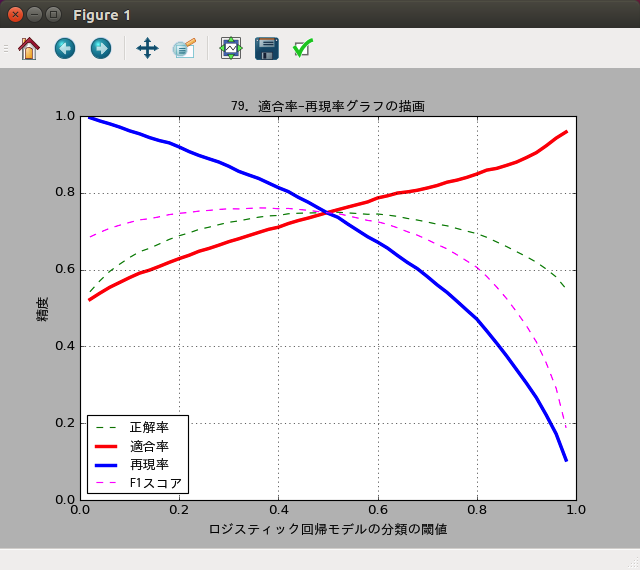
実行結果:
ロジスティック回帰の閾値
問題74の「予測の方法」に書いたように、これまでは仮設関数の結果が0.5より大きいかどうかで肯定的か否定的かを振り分けていました。この0.5という閾値を変化させて、適合率や再現率がどう変わるかをグラフで示せという問題のようです。
実装について
問題78の結果ファイル「result.txt」を使いまわすことにしました。このファイルは問題76のフォーマットになっているため、3カラム目の予測確率を元の仮説関数の
値に逆算して戻します。そして閾値を変えながら予測ラベルを計算し直すことを繰り返しました。
問題77で作ったscore()も使いまわした関係で正解率とF1スコアも同時に計算できます。そのため、それらもグラフに加えてみました。
グラフの描画
グラフはmatplotlibを使って描きました。問題37で棒グラフ、問題38でヒストグラム、問題39で散布図を描きましたが、今回はpyplot.plot()で折れ線グラフを描いています。
結果について
まず適合率についてです。
問題77の「正例に関する適合率」に書いたように、適合率は否定的なものを肯定的と予測してしまうと下がりますが、肯定的なものを否定的と予測してしまっても下がりません。つまり、確実に肯定的だと思うものだけを肯定的と予測すれば上がります。閾値が大きくなればなるほどこの傾向になるため、閾値が大きくなるのに合わせて適合率も高くなるグラフになりました。
なお、閾値が0の場合は全部肯定的と予測することになり適合率は最低になります。ただこの場合でも実際に半分は肯定的なレビューなので正解になります。そのため適合率は50%が最低で、これ以上悪くなることはありません。
続いて再現率です。
問題77の「正例に関する再現率」に書いたように、再現率は肯定的なものを見逃さなければ高くなるため、怪しいものはとにかく全部肯定的だと予測すれば上がります。閾値が小さければ小さいほどこの傾向になるため、閾値が小さくなるのに合わせて再現率が高くなるグラフになりました。
なお、閾値が0の場合は全部肯定的と予測するため見逃しはなくなり再現率は100%です。閾値1の場合は全部否定的になって全部見逃すことになるため再現率は0%になります。
ついでに描いてみたF1スコアのグラフは、だいたい適合率と再現率のバランスをとった感じになっていますね。
80本目のノックは以上です。誤りなどありましたら、ご指摘いただけますと幸いです。
実行結果には、100本ノックで用いるコーパス・データで配布されているデータの一部が含まれます。