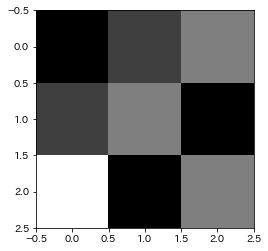画像処理ライブラリに頼らず、行列演算だけで画像処理をするお話。Pythonistaでも可能
中級編たち
図形描画・グレースケール化・畳み込みフィルタリング・アフィン変換
前置き
「再発明家」とは
Open CVとかPillowに頼らず、numpyとmatplotlibを使って、様々な画像処理を実際に書いてみる。iOSアプリのPythonistaでも使える組み合わせだ。
実行環境
標準ライブラリのほかに、numpyとmatplotlibを使う。pandasとかscipyは使っていない。この組み合わせはmatlabユーザーにも取っつきやすい文法だと思われる。
Windows10でPython 3.5.2|Anaconda 4.2.0のnumpy 1.12.1|matplotlib 2.0.0
Pythonista3でnumpy 1.8.0|matplotlib 1.4.0
で動作確認している。
import numpy as np
import matplotlib.pyplot as plt
前提知識
python 3の知識とnumpy、matplotlibの知識を前提としている。(あとは、numpyと付属して、行列の知識とか)
基礎編
画像を読み込む・表示する・保存する
画像の読み込み、表示、保存にはmatplotlib.pyplotを使う。また、読み込んだ画像はnumpy.ndarrayに格納される。
今回は同じディレクトリ内のlabyrinth.jpegの読み書きをしてみよう。
# 画像の読み込み
# imgに三次元のnp.arrayの配列が格納される。
img = plt.imread('labyrinth.jpeg')
type(img) #=> numpy.ndarray
img.size #=> (1367, 1345, 3)
# 画像の表示
plt.imshow(img)
plt.show() #使った画像が小さいときはボケて見えるけど今は気にしないで
# 画像の保存
plt.imsave('labyrinth-1.jpeg', img) #拡張子を.pngとかに変えてもちゃんと保存してくれる。
横の目盛りは、保存の時にはないので安心してほしい。
これで入力と出力とデバッグ手段を手に入れたといっても過言ではない。
ピクセルの自作
自分でピクセルを指定して、画像を作りたい、と考える人もいるかもしれない。
そんな時は、2次元ないし3次元のnp.arrayでピクセルを指定すればいいのだが、ここでちょっとしたコツが必要なので紹介しておく。
白黒画像 ((高さ=3)*(横幅=3)の二次元配列)
img_gray = np.array([
[0,63,127],
[63,127,0],
[255,0,127]
], dtype = np.uint8)
# 画像の表示
plt.imshow(img_gray, cmap = 'gray', vmin = 0, vmax = 255, interpolation = 'none')
plt.show()
まずは白黒画像。ここで4か所ほど、わけわからないところがある。
dtype = np.uint8cmap = 'gray'vmin = 0, vmax = 255interpolation = 'none'
である。
それぞれ解説していこう。
(1と3は合わせて解説する)
dtype = np.uint8, vmin = 0, vmax = 255
カラーピッカーを使ったことがあれば、色はよく0~255の間で表される事がわかるだろう。
しかし、これをpltに伝えるにはあの手この手が必要である。
dtypeの指定は実は今回、不要である。これはむしろ、カラーの時に役立つ指定であるが、つけておいて損はないと思われる。
白黒画像には、vmin, vmaxの指定が必要である。
これを抜かすと、imshow()で勝手に正規化されてしまうからだ。
cmap = 'gray'
cmapがcolormapという略であることと、grayが灰色という意味であることを考えると、大体予想つく。
つまり、一次元データを黒-灰色-白と解釈させるための指定である。
これを試しにこの中のどれかに変えてみると、解釈が変わって色味も変わる。(例えばYlOrBr_rを使うとセピアっぽい)cmapを自作する事も可能である。
interpolation = 'none'
これは、勝手にかかってるフィルターを外すものである。(というかアンチエイリアス)なぜ最初からかかっているのかは知らないが、少なくとも各ピクセルが思い通りの色になっていることを確認するうえで邪魔なので外しておく。
なお、たぶんこれはバージョンによって何がかかっているかが変わる。
RGB画像 ((高さ=3)(横幅=3)(RGB)の三次元配列)
img_rgb = np.array([
[[255,0,0],[0,255,0],[0,0,255]],
[[255,255,0],[0,255,255],[255,0,255]],
[[0,0,0],[127,127,127],[255,255,255]],
], dtype = np.uint8)
# 画像の表示
plt.imshow(img_rgb, cmap = 'gray', vmin = 0, vmax = 255, interpolation = 'none')
# => plt.imshow(img_rgb, interpolation = 'none') と同じ
plt.show()
コードは先ほどとほとんど変わらない。(cmapやvmax, vminを指定しても無視される)
RGBA画像 ((高さ=3)(横幅=3)(RGBA)の三次元配列)
img_rgba = np.array([
[[255,0,0,0],[0,255,0,0],[0,0,255,0]],
[[255,0,0,127],[0,255,0,127],[0,0,255,127]],
[[255,0,0,255],[0,255,0,255],[0,0,255,255]],
], dtype = np.uint8)
# 画像の表示
plt.imshow(img_rgba, cmap = 'gray', vmin = 0, vmax = 255, interpolation = 'none')
# => plt.imshow(img_rgba, interpolation = 'none') と同じ
plt.show()
同じくコードは先ほどとほとんど変わらない。
念のため記述しておくと、RGBAのAは透明度を表すアルファのAである。
これは上の画像を見ても透過しているかわかりにくいが、gimpなどでみると、透明であることがよくわかる。
これらをまとめた関数をとりあえず作っておく。
def img_show(img : np.ndarray, cmap = 'gray', vmin = 0, vmax = 255, interpolation = 'none') -> None:
'''np.arrayを引数とし、画像を表示する。'''
#dtypeをuint8にする
#オーバーフロー、アンダーフローの処理
img = np.clip(img,vmin,vmax).astype(np.uint8)
#画像を表示
plt.imshow(img, cmap = cmap, vmin = vmin, vmax = vmax, interpolation = interpolation)
plt.show()
plt.close()
以上で、自分でドット絵が作れるようになった。
拡大(単純な拡大)
ここで扱う拡大は整数倍、補間なしの拡大である。
repeatを使う。
# 縦方向に5、横方向に3倍拡大
# 画像の読み込み
img = plt.imread('labyrinth.jpeg')
# 画像の拡大
img_expand = img.repeat(5, axis = 0).repeat(3, axis = 1)
img_show(img_expand)

パッと見、横方向に縮んでいるが、目盛を見れば拡大されている。(img_expand.sizeで確認してもよい)
これはあまり使われない拡大であり、実際に使われている拡大は後述される。(予定)
画像を並べる
同じ画像を横に並べたり、縦に並べたりしてみよう。concatenateが便利だ。
img = plt.imread('labyrinth.jpeg')
img_verticle = np.concatenate((img, img), axis = 0) #縦
img_horizontal = np.concatenate((img,)*3, axis = 1) #横
# 画像の表示
img_show(img_verticle)
img_show(img_horizontal)
横の画像ではタプルに乗算を施すことで、繰り返しの回数を指定している。
四角形にトリミング (3/30追加)
インデックス操作でトリミングは簡単にできる。
img = plt.imread('labyrinth.jpeg')
# 縦に1000:1500、横に0:500を切り出す
img_show(img[1000:1500,0:500])
RGB分解
def decomposition(img : np.ndarray, channel : list = [1.,1.,1.]) -> np.ndarray:
'''channelに与えられた強度でチャンネルごとに強調する'''
float_img = img * channel
return np.array(float_img,dtype = np.uint8)
img = plt.imread('labyrinth.jpeg')
img_show(decomposition(img, [1.,0.,0.]), cmap = 'Reds')
img_show(decomposition(img, [0.,1.,0.]), cmap = 'Greens')
img_show(decomposition(img, [0.,0.,1.]), cmap = 'Blues')



上のコードではdecomposition(チャンネル分解は英語でcolor decompositionというらしい)という関数を定義している。これは基本的にはimg*[0,0,1]という操作をしているが、型が若干複雑なため、関数を定義した。
念のためにgimpで確認してみたが、見た感じ同じだった。
グレースケール化
RGBの3次元の値を持ったピクセルをYの1次元の値のみを持つピクセルに変換することをグレースケール化という。要するに、白黒画像を作る手法である。
様々なグレースケールの手法があるが、ここでは、中間値法とGチャンネル法のみを扱う。
中間値法
中間値法はRGBの中の最大値とRGBの中の最小値の平均をYとして用いる。
つまり、(max(R,G,B) + min(R,G,B)) / 2みたいな計算が行われる。
img = plt.imread('labyrinth.jpeg')
img_mid_v = np.max(img, axis = 2)/2 +np.min(img, axis = 2)/2
img_show(img_mid_v)
ここで、一点。img_mid_vの計算式について
img_mid_v = (np.max(img, axis = 2) + np.min(img, axis = 2))/2ではだめなのか、という疑問が湧くかもしれない。答えは「だめなのだ」である。理由は 最大値と最小値を先に足すと、uint8がオーバーフローするからである。なお、型はfloatになった後、img_showでuint8に戻る。
ちなみに、np.max(img, axis = 2)//2 + np.min(img, axis = 2)//2でも大して変わりはないが、最小値と最大値でそれぞれ切り捨てが行われることに気を付けたい。
Gチャンネル
人間はRGBのうち、Gを一番強く認識しているらしい。これに注目したのが、Gチャンネル法である。
Gチャンネル法では、Gの値をYの値とみなす。要するにすごい荒っぽいやり方であるが、そこそこ有効なので人間は不思議なものである。(網膜の上だとRもGも同じくらいの錐体細胞があるはずなのでなおさら不思議)
コードは簡単である。なお...はEllipsisという便利な記号である。
img = plt.imread('labyrinth.jpeg')
img_g_channel = img[...,1]
img_show(img_g_channel)
先ほどのRGB分解と発想は同じである。にしても、この単純な手法が当たらずとも遠からずなのが悔しい。
ほかの手法については今後扱っていく予定である。
二値化
白黒画像を得られたことだし、Yの値が「閾値以上のピクセルを1、未満のピクセルを0」とする、二値化をやってみる。白黒画像はGチャンネル法で作ったものを使う。
img = plt.imread('labyrinth.jpeg')
img_g_channel = img[...,1]
# 閾地の設定
threshold = 75
img_binary = img_g_channel >= threshold
img_binary = np.uint8(img_binary * 255)
img_show(img_binary)
なんとなく、迷路が浮き上がっている気がする。
畳みこみによるフィルター
基礎編の最後として、畳み込みによるフィルターの作り方を紹介する。
畳み込みによるフィルターは空間フィルタリング がわかりやすい。
今回用いるフィルターは以下2つの行列による畳み込みを使う。
\frac{1}{256}\left(
\begin{matrix}
21 & 31 & 21 \\
31 & 48 & 31 \\
21 & 31 & 21
\end{matrix}
\right)
これはぼかしを行うフィルターであり、よくガウスぼかし、と呼ばれるものである。
これは輪郭抽出に先立って、ノイズ除去のためによく使われるフィルターである。
\left(
\begin{matrix}
0 & -1 & 0 \\
-1 & 4 & -1 \\
0 & -1 & 0
\end{matrix}
\right)
これはラプラシアンフィルターであり、輪郭抽出によく用いられる。on centerの双極細胞と発想は同じ、と言う表現がわかりやすい人は果たしてここまでたどり着けているだろうか…
まず、2次元配列を畳み込みをするための関数を作成する(scipyやPILを使うと自作する必要はないが、残念ながら、Numpyとmatplotlibという縛りの条件下では自作するよりほかない。
def convolve2d(img, kernel):
#部分行列の大きさを計算
sub_shape = tuple(np.subtract(img.shape, kernel.shape) + 1)
#関数名が長いのでいったん省略
strd = np.lib.stride_tricks.as_strided
#部分行列の行列を作成
submatrices = strd(img,kernel.shape + sub_shape,img.strides * 2)
#部分行列とカーネルのアインシュタイン和を計算
convolved_matrix = np.einsum('ij,ijkl->kl', kernel, submatrices)
return convolved_matrix
上記コードはimgの部分行列の行列を使って畳み込みをしている。詳しくはstackoverflow先生を見てほしい。
# フィルターのカーネルの作成
gaussian = np.array([[21,31,21],
[31, 48,31],
[21,31,21]])/256
laplacian = np.array([[ 0,-1, 0],
[-1, 4,-1],
[ 0,-1, 0]])
# 画像の読み込み
img = plt.imread('labyrinth.jpeg')
img = img[...,1] # 今回はGチャンネルのみを対象とする。
# ガウスぼかしを20回かける
for _ in range(20):
img = convolve2d(img, gaussian)
この時点では端が切れている程度の変化に思えるかもしれないが、bmpで保存して拡大してみると意外に違うことがわかる。

# ラプラシアンフィルターをかける
img = convolve2d(img, laplacian)
plt.imshow(b,cmap = 'gray_r', vmax = img.max()*0.5)
# 最大値が255とは限らない。
# また、最大値に合わせると、ほかの値がつぶれたため、*0.5で補正。
plt.show()
plt.close()
ちょっとインパクトに欠けるので、基礎編のまとめをしておこう。
img = np.array([
[[ 0, 0, 0],[ 0, 63,127],[255, 0, 0]],
[[ 63, 63, 63],[ 0, 0,255],[ 0, 0, 0]],
[[255,255,255],[ 0, 0, 0],[ 63,127, 0]]
], dtype = np.uint8)
img = img.repeat(100,axis = 1).repeat(100,axis = 0)#拡大
img = np.concatenate((img,)*2, axis = 1) #横方向にコピー
img = np.concatenate((img,)*2, axis = 0) #縦方向にコピー
print('RGB画像')
img_show(img)
# 中間値法で白黒画像を生成
img = np.array(np.max(img, axis = 2)/2 +np.min(img, axis = 2)/2, dtype = np.uint8)
print('白黒画像')
img_show(img)
# ガウスぼかし
img = convolve2d(img, gaussian)
# 輪郭抽出
img = convolve2d(img, laplacian)
print('輪郭抽出')
plt.imshow(img,cmap = 'gray_r', vmax = img.max())
plt.show()
plt.close()
基礎編では、このほかGチャンネル法と二値化も見た。
中級編
※少しづつ追加するので、興味がある人はストックをしておいてください。
もう既に長すぎるので概略と目次にとどめました。詳しくはリンクに飛んでください。また、中級編から使う画像が変わります。なんたってどうして私は赤の入ってない画像を使ってたんだ…。
図形の描画 (3/30日追加)
図形を描画するには、mgridを用いることで、画像上の座標を取得する。
x, y = np.mgrid[:100,:100]
ここで、$x$の正方向が下、$y$の正方向が右向きであることに注意してほしい。
グレースケール化 (3/30日追加)
グレースケール化、とは各ピクセルに充てられたRGBの値を白黒の値Yを計算する手法である。
ここでは、基礎編で扱わなかった様々なグレースケールの手法も試してみる。
詳しい説明はリンクを参照。同じ順序で扱っている。
畳み込みフィルタリング (4/1日追加)
ローパスフィルター、ハイパスフィルター、微分フィルターを扱う。
アフィン変換 (4/5日追加)
画像をゆがませる方法はさまざまある。線形変換(拡大縮小・回転・剪断)と平行移動を合わせた変換をアフィン変換という。
詳しく学びたい人は