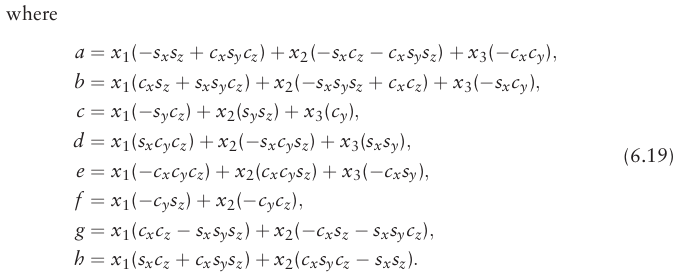はじめに
最適化(optimization)はロボット工学において非常に重要な技術であり、SLAM、経路計画、ロボットアーム運動など、さまざまな問題の解決に応用されている。
以前のシリーズでは、リー群とリー代数という概念について説明したが、今回は、実際の問題を通じて、リー群を用いた最適化について説明する。
前編
最適化
最適化は、ある目的を達成するために、与えられた制約のもとで最良の解を見つける問題である。ここの目的は、問題に応じて異なるが、例えば、最小二乗問題の目的は、残差の平方和を最小化することである。
最小二乗問題とは
最小二乗問題は最も基本的な最適化問題であり、式(1)のように定式化される。
$$
\underset{x}{\textrm{argmin}} \quad F(x) = \sum_{i=0}^{n} (r_i^T \Sigma^{-1} r_i) \tag{1}
$$
ここで、$r(x)$は残差関数であり、$x$は求めたいパラメータベクトルを表す。
最小二乗問題は、残差の平方和を最小化するため、最適なパラメータ$x$を探す。Fは目的関数(Objective function)もしくは損失関数(Loss function)と呼ぶ。
また、$\Sigma$はマハラノビス距離を計算する際の共分散行列であり、計算の重みと解釈とできる。$\Sigma$を単位行列にすると、一般的なユークリッド二乗($r^T r$)と一致する。
$$
\newcommand{\skew}[1]{[{#1}]_{\times}} %skew matrix
\newcommand{\so}[1]{ \mathfrak{so}{(#1)} } %lie algebra so3
\newcommand{\se}[1]{ \mathfrak{se}{(#1)} } %lie algebra se3
\newcommand{\norm}[1]{|{#1}|} %norm
$$
ガウス・ニュートン法
最小二乗問題を解決するため、様々な方法があるが、本文はガウス・ニュートン法をベースに説明する。
ガウス・ニュートン法は式(2)(3)のように、反復法を用いて$x$を更新し、更新量は$\Delta x$となる。
$$
\Delta x = -H^{-1}g
\tag{2}
$$
$$
x_{new} = x \boxplus \Delta x
\tag{3}
$$
式(3)の$\boxplus$は更新演算を定義する。式(2)の$g$と$H$はそれぞれ$r$の勾配ベクトルとヘッセ行列であり、ガウス・ニュートン法の場合、以下のように計算できる。
$$
g = \sum g_i= \sum J_i^T \Sigma^{-1} r_i \tag{4}
$$
$$
H = \sum H_i \approx \sum J_i^T \Sigma^{-1} J_i \tag{5}
$$
- $r$は残差ベクトル
- $J$は$r$のヤコビ行列である
まとめると、ガウス・ニュートン法の場合、$r$と$J$が計算できれば、反復法を用いて$x$を求めることができる。
最適化の実問題
次は、3D点群マッチングという実問題を用いて、リー群上の最適化について解説する。
3D点群マッチングでは、2つの点群$A$と$B$を剛体変換行列Tを用いて位置合わせする。$T$のパラメータ$x$を調整することで、$A$と$B$の位置の誤差を最小化することを目指す。この問題の残差関数$r$は式(6)のように定義できる。
$$
r = T(x)a - b\tag{6}
$$
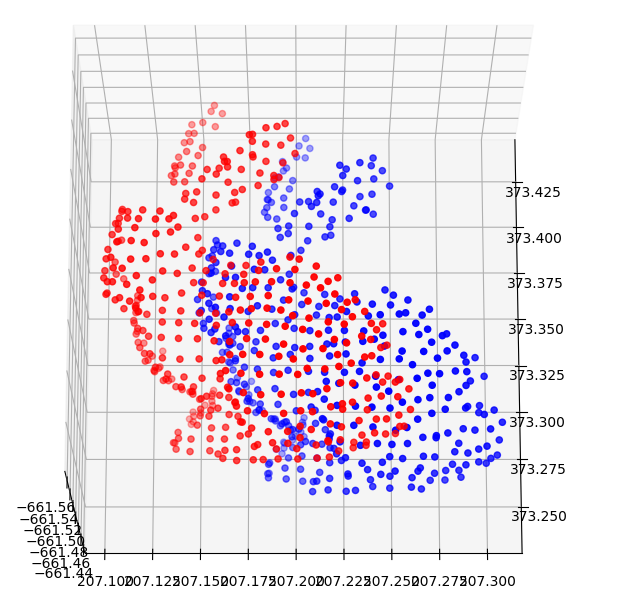
例として、図のように、赤い点群$A$と青い点群$B$を位置合わせしたいとする。しかし、ノイズが存在しているため、完璧な解(すべての$r$が0)が存在せず、$r$の合計を最小にする剛体変換行列を求めたい。
従来の方法
前章でも説明したが、rのヤコビ行列$J$が計算できれば、ガウス・ニュートン法でこの問題を解くことができる。
しかし、従来の(つまり、リー群を導入していない) $J$の計算は非常に煩雑である。有名なNDTの論文(magnusson 2009)の6.17~6.19では$J$の詳細な計算方法が示されている。
$s$と$c$はそれぞれ$\sin$と$\cos$を表し、$\sin$と$\cos$がたくさん掛け算されている。この計算は複雑で、見るだけでも大変さがわかるだろう。詳細な計算は本文で使わないので、無視してください。
リー群を使う方法
次はリー群を使用してヤコビ行列$J$の計算方法を導出する。ここから前編の知識が必要なので、必要であれば前編を読んでください。
$SE(3)$上の更新$\boxplus$は以下のように定義される。
$$
T(x_{0}\boxplus\delta) \triangleq T(x_{0})\exp( \delta ) \tag{7}
$$
ここで、$\delta \in \se3$は小さな更新量を表し、$x_{0}$は更新前の状態を示す。
$\delta$が小さい場合、$\exp( \delta )$は一次展開によって近似できる。
$$
T(x_{0}\boxplus\delta) = T_{0}\exp( \delta ) \cong T_{0} + T_{0}\widehat{\delta} \tag{8}
$$
ヤコビ行列$J$は、残差関数$r$の各成分に対する偏微分を表すため、微分の一般定義に(8)を代入すると以下のようになる。
$$
\begin{aligned}
J &= \lim_{\delta \to \mathbb{0}} \frac{(T_{0}\exp\left( \delta \right)a - b)- (T_{0}a-b)}{\delta} \\
&\cong \lim_{\delta \to \mathbb{0}}\frac{T_{0}a + T_{0}\widehat{\delta}a - T_{0}a}{\delta} \\
&= \lim_{\delta \to \mathbb{0}}\frac{T_{0}\widehat{\delta}a}{\delta} \
\end{aligned}
\tag{9}
$$
$\delta$は回転成分$\omega$と並進移動成分$\rho$に分解することができる。
$$\delta = [\rho, \omega ] \tag{10}$$
式(9)に$\delta$の分解を代入し、簡略化計算を行うと、最終的に以下のようなヤコビ行列の式 (11) を得ることができる。
$$
\quad \quad J= \lim_{\delta \to \mathbb{0}} \frac{T_{0}\begin{bmatrix}[ \omega ]_{\times} & \rho \\
0 & 0 \\
\end{bmatrix}
\begin{bmatrix}
a \\
1
\end{bmatrix}}
{[\rho,\omega ]}
$$
$$
\quad\quad\quad\quad = \lim_{\delta \to \mathbb{0}} \frac{T_{0}
\begin{bmatrix}
I & [ - a ]_{\times} \\
0 & 0
\end{bmatrix}\begin{bmatrix}
\rho \\
\omega
\end{bmatrix}}{[\rho,\omega ]}
$$
$$
= T_{0}\begin{bmatrix}
I & [ - a ]_{\times} \\
0 & 0
\end{bmatrix}
\tag{11}
$$
最終の$J$は非常にシンプルで美しいよね。NDT論文の6.17〜6.19と比較すると、$\sin$や$\cos$が一切登場せず、実際のアプリケーションでも高速に実装することができる。
Pythonで実践してみよう
次は、Pythonを使って、三次元点群のマッチング問題の最適化を実践してみよう。式(6)と式(11)で定義された3D点群マッチング問題の残差関数$r$とヤコビ行列を次のPythonコードで簡単に計算できる。
def residual(x, a, b):
T0 = expSE3(x)
R, t = makeRt(T0)
r = R.dot(a) + t - b # r残差関数 式(6)
I = np.eye(3)
tmp = np.zeros([4, 6])
tmp[0:3, 0:3] = I
tmp[0:3, 3:6] = skew(-a)
J = (T0 @ tmp)[0:3] #ヤコビ行列 式(11)
return r.flatten(), J
残差関数$r$とヤコビ行列を使って、反復法で$x$を計算できる。
# A, B は2つの点群
for i in zip(A, B):
r_i, j_i = residual(x, a, b) #rとJの計算
H += j_i.T.dot(j_i) #式(5) ヘッセ行列の計算
g += j_i.T.dot(r_i) #式(6) 勾配ベクトルの計算
dx = np.linalg.solve(H, -g) #式(2) ガウス・ニュートン法より更新量の計算
x = x @ expSE3(dx) #式(7) 更新量を用いて、xを更新する
以下の図は点群マッチングのデモである。初期位置を遠く離れた場所に設定しても、非常に速く収束することがわかる。
まとめ
今回は3D点群マッチングという実問題を用いて、リー群上の最適化について説明した。
リー群の$\exp$展開は容易に線形化ができるため、リー群を導入すると最適化問題のヤコビアン行列が美しい線形形式となり、最適化計算も高速に実装することができる。
もちろん、問題定義(残差関数)が変わると、ヤコビアン行列の計算も変わるが、$\exp$関数の線形化を利用し、式(9)~(11)を参考することで、他の問題のヤコビアンも容易に導出できるだろう。
本文デモの実装はgithubに公開していますので、ご自由に参考にしてください。
- 2d 点群マッチング:guass_newton_method/demo_2d.py
- 3d 点群マッチング:guass_newton_method/demo_2d.py