#はじめに
Pythonを用いた楕円型偏微分方程式の解法について述べる。
Qiita記事
[Pythonによる科学・技術計算] 静電位に対する2次元ラプラス・ポアソン方程式のヤコビ法による数値解法,楕円型偏微分方程式,境界値問題 [1]
ではヤコビ法を用いてラプラス方程式を解いた。ヤコビ法は収束が遅く実用的ではない,とされる。
本稿ではヤコビ法よりも速いとされるガウス-ザイデル法および逐次過緩和法(SOR法)をもちいてラプラス方程式を解き,収束速度を比較する。
結論: (最適な条件下で)SOR法が圧倒的に速い
手法については補遺に簡単にまとめたので参考にされたい。
#内容
Qiita記事で用いた計算コードとほとんど同じものを用い,
ヤコビ法,ガウス-ザイデル法,SOR法の収束速度を比較する。
具体的には,メッシュ数Nに対する反復回数をそれぞれのスキームで調べる。
Nは, N=100, 1000, 10000, 100000の4点を選んだ。
SOR法は特別な場合にガウス-ザイデル法になる。
%%time
"""
ラプラス方程式: 数値解法, SOR法:
ω = 1でガウス-ザイデル法になる
長方形領域
14 Aug. 2017
"""
#%matplotlib nbagg
import numpy as np
import matplotlib.pyplot as plt
#
delta_Lx=0.03
delta_Ly=0.03
LLx = 10 # 長方形の幅 (x方向)
LLy= 10 # 長方形の幅 (y方向)
Lx = int(LLx/delta_Lx)
Ly = int(LLy/delta_Ly)
V = 2.0 # 電圧
convegence_criterion = 10**-5
phi = np.zeros([Lx+1,Ly+1])
phi_Bound= np.zeros([Lx+1,Ly+1])
phi_Bound[0,:] = V # 境界条件
# for SOR method
aa_recta=0.5*(np.cos(np.pi/Lx)+np.cos(np.pi/Ly)) #
omega_SOR_recta = 2/(1+np.sqrt(1-aa_recta**2)) # 長方形領域に対する最適加速パラメータ
print("omega_SOR_rect=",omega_SOR_recta)
# メイン
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
phi_in=phi.copy()
if n_iter % 40 ==0: # 収束状況のモニタリング
print("iteration No =", n_iter, "delta=",delta)
conv_check.append([n_iter, delta])
for i in range(Lx+1):
for j in range(Ly+1):
if i ==0 or i ==Lx or j==0 or j==Ly:
phi[i,j] = phi_Bound[i,j]
else:
phi[i,j] = phi[i,j]+omega_SOR_recta *((phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4-phi[i,j]) # SOR法による更新
delta = np.max(abs(phi- phi_in))
n_iter+=1
print ("The number of total iteration =",n_iter)
print("data_points=",Lx*Ly)
#for plot
plt.xlabel('X')
plt.ylabel('Y')
plt.imshow(phi,cmap='hsv')
plt.show()
#結果 (1) 解の表示
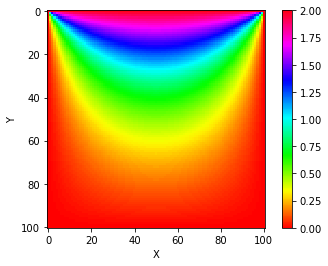
まず,ラプラス方程式の解そのものを以下の図にしめす。これはQiita記事で得られている。100x100メッシュで計算した。
#結果 (2) 収束速度の比較
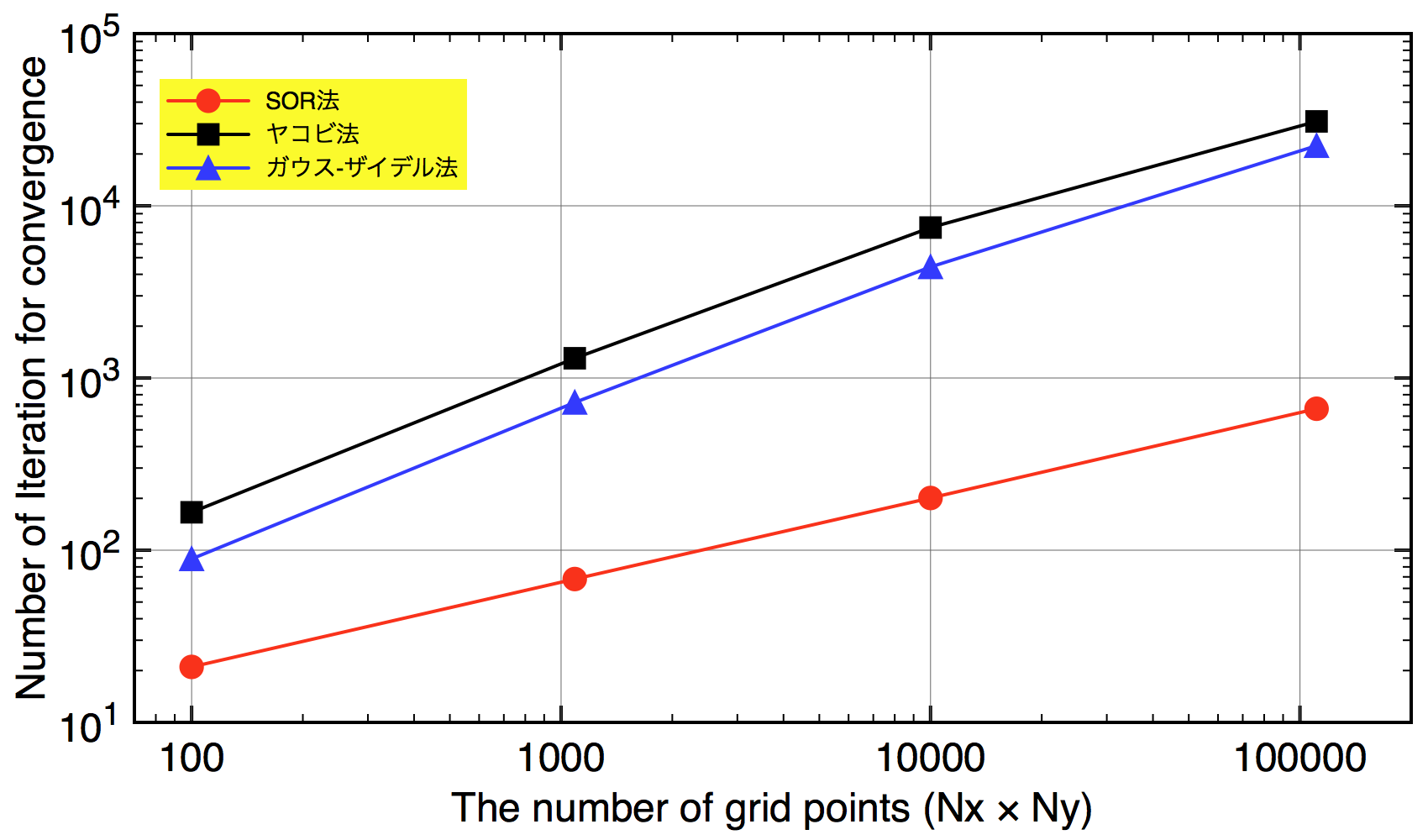
収束するまでにかかった反復回数のデータ点数($Nx\times Ny$)依存性を表に示す。
| グリッド数: $N\times N$ | SOR法 | ガウス-ザイデル法 | ヤコビ法 |
|---|---|---|---|
| 100 (10x10) | 21 | 89 | 166 |
| 1089 (33x33) | 68 | 721 | 1302 |
| 10000 (100x100) | 201 | 4416 | 7476 |
| 110889 (333x333) | 663 | 22334 | 30913 |
圧倒的にSOR法が速いことがわかる。
また,期待されたように[補遺]**SOR法の反復回数がNに比例していることもわかる。
ガウスザイデル法の収束速度はヤコビ法と比べて2倍程度速い。だがそれでもSOR法との顕著な速度差があり,実用面には乏しい。
この表を両対数グラフにしたものを以下に示す。傾きが反復回数のグリッド点数依存性を示している。
横軸はグリッド点数,縦軸が収束するまでに要した反復回数を示している。直線的な変化は,反復回数のグリッド点数依存性のべき指数が一定であることを示している。SOR法の傾きはガウス-ザイデル・ヤコビ法とくらべ小さく,収束次数が大きいことが分かる。
#結論
最適な加速パラメータが分かっているのならSOR法を使うべき。
現実的な計算($Nx, Ny \gt$100)でガウスザイデル法と比べ20倍以上高速になる。
#補遺
##補遺(1): ガウス-ザイデル法: -ヤコビ法の若干の改善-
ガウス-ザイデル法は,Qiita記事の補遺にあるヤコビ法による式(12)
$
\phi(x_i,y_j) = \frac{1}{4} [\phi(x_{i+1},y_{j})+\phi(x_{i-1},y_{j})+\phi(x_{i},y_{j+1})+\phi(x_{i},y_{j-1})]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2
$
の$(n+1)$ステップ目の表現
$
\phi(x_i,y_j)^{(n+1)} = \frac{1}{4} [\phi(x_{i+1},y_{j})^{(n)}+\phi(x_{i-1},y_{j})^{(n)}+\phi(x_{i},y_{j+1})^{(n)}+\phi(x_{i},y_{j-1})^{(n)}]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2 \tag{1}
$
において, $\phi(x_{i-1},y_j)^{(n)} $ と$\phi(x_{i},y_{j-1})^{(n)} $は実は事前に更新されているので,$n$ステップ目の値を使わず,
$\phi(x_{i-1},y_j)^{(n+1)} $と$\phi(x_{i},y_{j-1})^{(n+1)} $を使う方法である。つまり,
$
\phi(x_i,y_j)^{(n+1)} = \frac{1}{4} [\phi(x_{i+1},y_{j})^{(n)}+\phi(x_{i-1},y_{j})^{(n+1)}+\phi(x_{i},y_{j+1})^{(n)}+\phi(x_{i},y_{j-1})^{(n+1)}]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2 \tag{2}
$
とする。これは,逐次$\phi(x_i,y_j)$ を更新していくためヤコビ法と比べてコードのメモリ使用も節減できる
ヤコビ法より若干(大きなメッシュに対して反復回数がヤコビ法の半分程度になる[1])収束が速くなると期待できるが,この方法でも収束が遅い。
##補遺(2): 数値解法: SOR法: -ヤコビ法の若干の改善-
実用的なアルゴリズムの一つに逐次過緩和法(SOR法[2])がある。
以下にみるように,この方法はガウス-ザイデル法による$\phi(x_i,y_j)^{(n)} $の更新を加速パラメータ$\omega$をかけて加速させる方法である。
ガウス-ザイデル法の反復過程は以下のようにかきなおせる[1]。
$\phi(x_i,y_j)^{(n+1)} = \phi(x_i,y_j)^{(n)}+\Delta \phi(x,y)^{(n)} \tag{3}$
$\Delta \phi(x,y)^{(n)}=\frac{1}{4} [\phi(x_{i+1},y_{j})^{(n)}+\phi(x_{i-1},y_{j})^{(n)}+\phi(x_{i},y_{j+1})^{(n)}+\phi(x_{i},y_{j-1})^{(n)}]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2-\phi(x_i,y_j)^{(n)} \tag{4}$
ここで$\Delta \phi(x,y)$はガウス-ザイデル法による$\phi(x,y)^{(n)}$の更新量を表している。
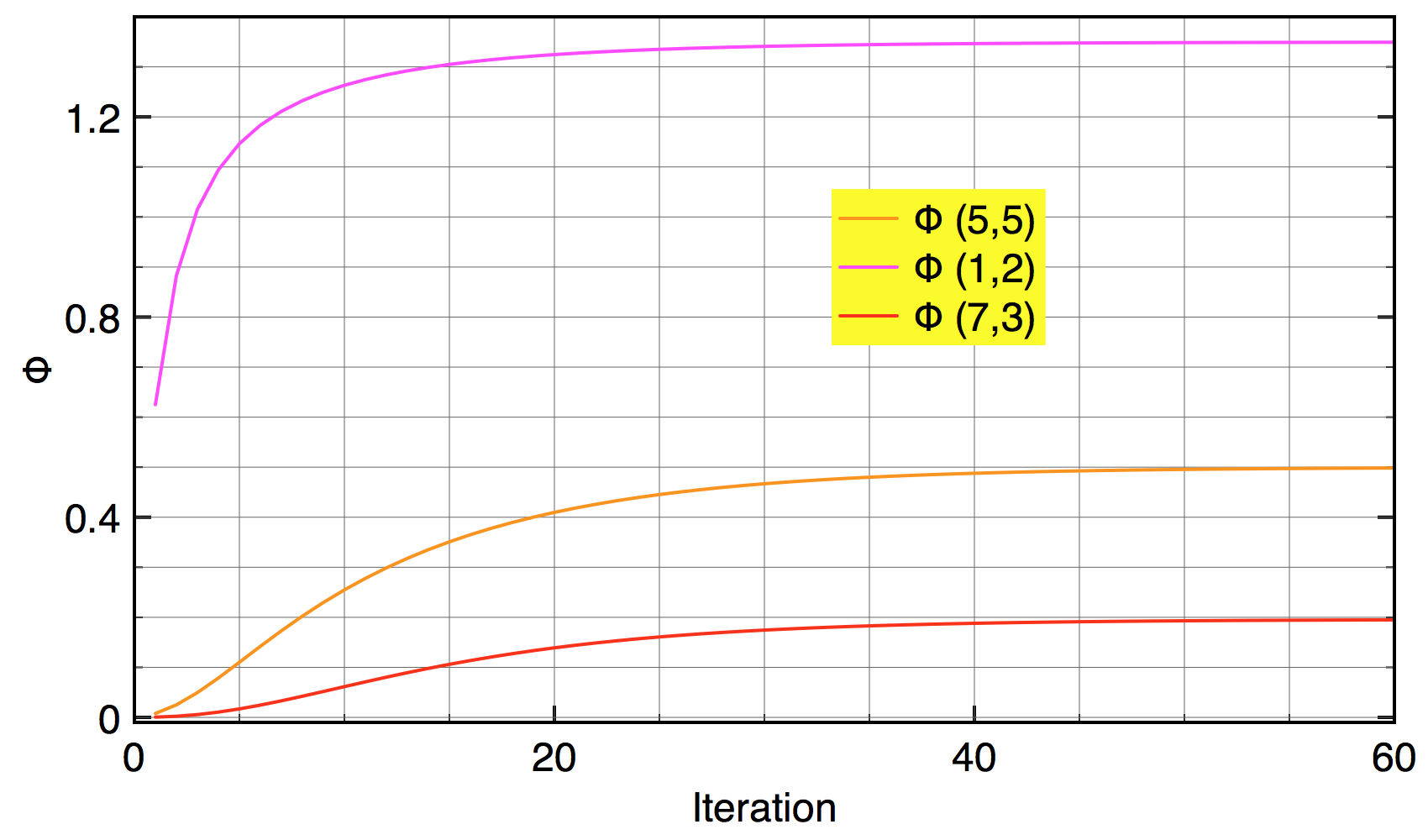
さて,ガウス-ザイデル法では, $\phi(x,y)^{(n)}$が反復過程で単調に変化することが多い。例として, 10x10メッシュでラプラス方程式を解いたときの幾つかの$\phi$の値の反復過程における変化を図に示す。単調変化していることがわかるだろう。
**SOR法はこの単調変化を積極的に活用する方法である。$\phi$が単調に変化するのだから,ガウス-ザイデル法が予言する更新量$\Delta \phi(x,y)$ (式(4))をもっと大きくして収束速度を上げることができそうである。**このアイディアがSOR法のエッセンスである。
そこで式(4)の$\Delta \phi(x,y)$を$\omega_{SOR}$倍した反復過程
$
\phi(x_i,y_j)^{(n+1)} = \phi(x_i,y_j)^{(n)}+\omega_{SOR}[\frac{\phi(x_{i+1},y_{j})^{(n)}+\phi(x_{i-1},y_{j})^{(n)}+\phi(x_{i},y_{j+1})^{(n)}+\phi(x_{i},y_{j-1})^{(n)}}{4} +\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2-\phi(x_i,y_j)^{(n)}]\tag{5}
$
を考える。
これがSOR法である。$\omega_{SOR}$は過緩和パラメータと呼ばれる。$\omega_{SOR}$=1のときにガウス-ザイデル法になる。
$\omega_{SOR}$の与え方には任意性がある。最適(収束率が最も良い)なものを選べればガウス-ザイデル法よりも極めて収束が速くなる場合がある。最良の$\omega_{SOR}$を探すさまざまな方法が調べられている[2]。
長方形領域のラプラス(ポアソン)方程式に関しては最適な$\omega_{SOR}$がわかっており,
$\omega_{SOR} = \frac{2}{1+\sqrt(1-\lambda^2)}\tag{5}$
$\lambda=\frac{1}{2}[cos\frac{\pi}{N_x}+cos\frac{\pi}{N_y}] \tag{6}$
である。十分大きなグリッド $Nx\times Ny >>1$に対して$\omega_{SOR} \approx 2$となる。
$Nx=Ny=N$としよう。このとき,SOR法を用いた計算の収束に必要な反復回数は$N^1$に比例する。ヤコビ法やガウスザイデル法のそれは$N^2$に比例する。Nが十分大きいとき,SOR法の収束速度はガウス-ザイデル法・ヤコビ法よりも著しく速くなる[2]。本稿で調べた結果はこのことを強くサポートしている。
なお,実装は容易である。$\omega_{SOR}$をつかって式(5)をそのまま
phi[i,j] = phi[i,j]+omega_SOR*((phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4-phi[i,j])
と書くだけでよい[2]。
#参考文献
[1] 私のQiita記事, [Pythonによる科学・技術計算] 静電位に対する2次元ラプラス・ポアソン方程式のヤコビ法による数値解法,楕円型偏微分方程式,境界値問題
[2] 「ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ」技術評論社,1993.