はじめに
**Pythonで楕円型偏微分方程式を数値的に解く。**ラプラス方程式は電磁気学にとどまらず,物理学で広く応用されることから,学習価値は大きいだろう。物理以外でも,偏微分方程式の境界値問題の数値解法という点で学べることがあると思う。ただし本計算で用いた手法は収束が遅く実用的ではない。さらに高速な数値解法がある[2]。
本稿では2次元ラプラス方程式およびポアソン方程式を差分化し,繰り返し法で電位を決定する(ヤコビ法)。得られた電位から電場も求める。なお,方程式の導出とアルゴリズムの概略は[補遺]にまとめた。興味のある方は参照されたい。
● [追記]2017年8月14日
SOR法でポアソン方程式を解くコードを掲載した(参考文献の下のほう)。
ヤコビ法よりも50倍以上高速である。
例題の問題設定
例題(1)
ラプラス方程式を解く。
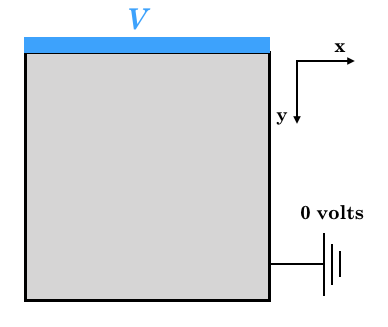
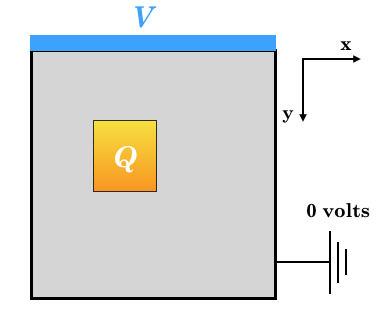
境界条件は図に示したとおり,y=0で\phi=Vボルト与えている。それ以外の境界でアースされ,0ボルトになっている。このときの静電位を決定し可視化する。
例題(2)
ポアソン方程式を解く。
例題(1)で考えた領域の中に外部電荷Qを入れる。このときの静電位$\phi$と電場$E = - \nabla \phi$を求め可視化する。
例題(1) ポアソン方程式
コード中,アニメーションも生成されるようにしている。解\phi(x,y)の収束していく様子を調べるためである。
追記 2017年12月17日: jupyter上での動作を想定している。jupyterを使わない場合はコード中の"%matplotlib nbagg"をコメントアウトすること。masa_stone22さまのご指摘より。
"""
ラプラス方程式: 数値解法, ヤコビ(Jacobi)法:
12 Aug. 2017
"""
%matplotlib nbagg
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation # アニメーション作成のためのメソッドをインポート
fig = plt.figure()
anim = []
#
delta_L=0.1 # グリッド幅
LL = 10 # 正方形の幅
L = int(LL/delta_L)
V = 5.0 # 1辺の境界の電位
convegence_criterion = 10**-3 # 収束条件。 精度を上げるならこの値を小さくする。
phi = np.zeros([L+1,L+1])
phi[0,:] = V # 境界条件
phi2 = np.empty ([L+1,L+1])
# for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])
# メイン
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
if n_iter % 100 ==0: # 収束状況のモニタリング
print("iteration No =", n_iter, "delta=",delta)
conv_check.append([n_iter, delta])
for i in range(L+1):
for j in range(L+1):
if i ==0 or i ==L or j==0 or j==L:
phi2[i,j] = phi[i,j]
else:
phi2[i,j] = (phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4 # 補遺:式(11)を参照
delta = np.max(abs(phi-phi2))
phi, phi2 = phi2, phi
n_iter+=1
im=plt.imshow(phi,cmap='hsv')
anim.append([im])
# for plot
plt.colorbar () # カラーバーの表示
plt.xlabel('X')
plt.ylabel('Y')
ani = ArtistAnimation(fig, anim, interval=100, blit=True,repeat_delay=1000)
ani.save("t.gif", writer='imagemagick')
plt.show()
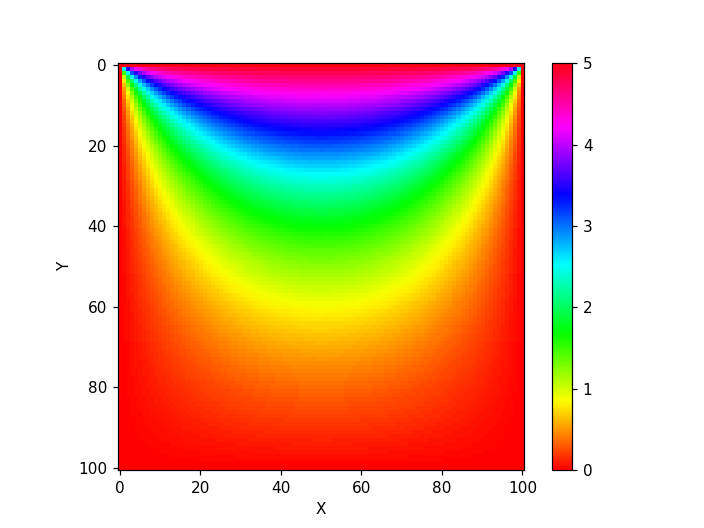
結果(1) ラプラス方程式の解
y=0の境界条件$\phi =5$を満たしている。境界近傍で電位の変化が大きい。
例題(2) 外部電荷を埋め込んだ場合のポアソン方程式の解
外部電荷密度$c=1000$,境界の電位を$V=5$とした。
"""
ポアソン方程式: ヤコビ(Jacobi)法
電場も表示:
12 Aug. 2017
"""
%matplotlib nbagg
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation # アニメーション作成のためのメソッドをインポート
anim = []
#
delta_L=0.01 #グリッド幅
LL = 1 # 正方形の幅
L = int(LL/delta_L)
V = 5.0 # 境界y=0の電位 (境界条件)
convegence_criterion = 10**-5
phi = np.zeros([L+1,L+1])
phi[0,:] = V # 境界条件
phi2 = np.empty ([L+1,L+1])
# 電荷密度の設定
eps0=1
charge= np.zeros([L+1,L+1])
c=1000 #電荷密度
CC=int(L/4)
CC2=int(L/2)
# 電荷密度をx=[L/4, L/2], y=[L/4,L/2]の領域に埋め込む
for i in range(CC, CC2+1):
for j in range(CC,CC2+1):
charge[i,j] = c
#
# for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])
# メイン
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
if n_iter % 100 ==0: # 収束状況のモニタリング
print("iteration No =", n_iter, "delta=",delta)
conv_check.append([n_iter, delta])
for i in range(L+1):
for j in range(L+1):
if i ==0 or i ==L or j==0 or j==L:
phi2[i,j] = phi[i,j]
else:
phi2[i,j] = (phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4 + (delta_L**2/(4*eps0))*charge[i,j]
delta = np.max(abs(phi-phi2))
phi, phi2 = phi2, phi
n_iter+=1
im=plt.imshow(phi,cmap='hsv')
anim.append([im])
# for plot
pp=plt.colorbar (orientation="vertical") # カラーバーの表示
pp.set_label("phi", fontname="Ariel", fontsize=24)
plt.xlabel('X',fontname="Ariel", fontsize=24)
plt.ylabel('Y',fontname="Ariel", fontsize=24)
plt.title('Solution of the Poisson equation for electrostatic potential ')
# ani = ArtistAnimation(fig, anim, interval=10, blit=True,repeat_delay=1000)
# ani.save("t.gif", writer='imagemagick')
plt.show()
# 電場の計算
Ex = np.zeros([L,L])
Ey = np.zeros([L,L])
for i in range(L):
for j in range(L):
Ex[i,j] = -(phi[i+1,j]-phi[i,j])/delta_L
Ey[i,j] = -(phi[i,j+1]-phi[i,j])/delta_L
plt.figure()
X, Y= np.meshgrid(np.arange(0, L,1), np.arange(0, L,1)) # メッシュ生成
plt.quiver(X,Y,Ex,Ey,color='red',angles='xy',scale_units='xy', scale=40) # ベクトル場をプロット
plt.xlim([0,L]) # 描くXの範囲
plt.ylim([0,L]) # 描くyの範囲
# グラフ描画
plt.grid()
plt.draw()
plt.show()
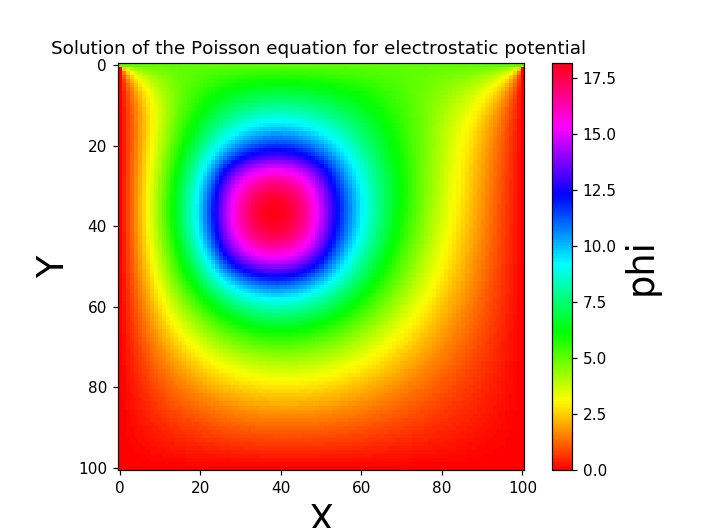
結果(2): 外部電荷を埋め込んだ系のポアソン方程式の解
y=0での境界条件は$\phi=5$である。埋め込んだ外部電荷により,例題(1)と比べて電位が大きく異なっている。
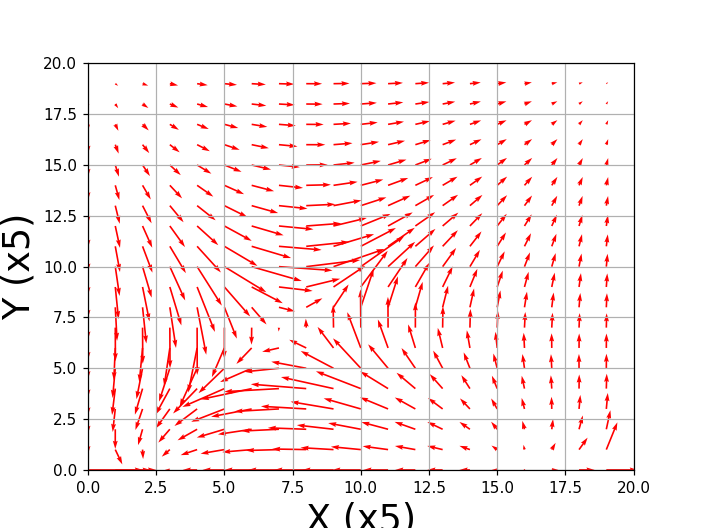
電場の様子。(#y軸が逆になってしまった)。この図はdelta_L=0.1として描いた。
電位の変動から期待されるように,外部電荷近傍で電場が大きく変動している。
補遺
補遺(1): 理論
静電場$E$と電位$\phi$の間になりたつ関係式
$E = - \nabla \phi \tag{1}$
と, 電荷密度$\rho$と$E$との間になりたつガウスの法則
$\nabla \cdot E =\frac{\rho} {\epsilon_0} \tag{2}$
を出発点とする。
(1)を(2)に代入すると
$\Delta \phi (x,y,z) =-\frac{\rho (x,y,z)} {\epsilon_0} \tag{3}$
を得る。これがポアソン(Poisson)方程式である。
ここで$\epsilon_0$は真空中の誘電率である。
空間のいたるところで真電荷が存在しない場合($\rho (x,y,z)=0$),ポアソン方程式は
$\Delta \phi (x,y,z) =0 \tag{4}$
となる。これがラプラス(Laplace)方程式である。
補遺(2): 数値解法: ヤコビ法
二次元を考える。
ポアソン方程式は
$ \frac{\partial^2 \phi(x,y)}{\partial x^2} + \frac{\partial^2 \phi(x,y)}{\partial y^2} =-\frac{\rho (x,y,z)} {\epsilon_0} \tag{5}$
となる。
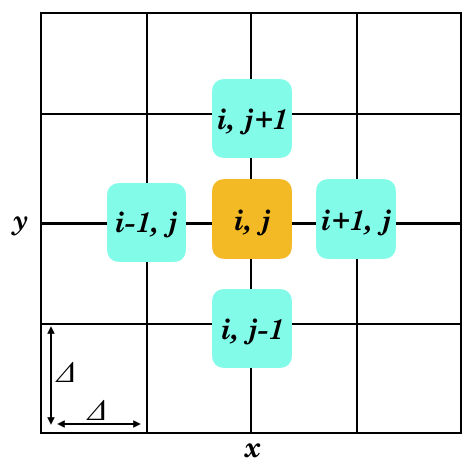
$x$および$y$方向に幅$\Delta$で区切られた2次元格子(下図参照)を考える。
点($x+\Delta,y$)で電位$\phi(x,y)$をテイラー展開すると,
$\phi(x+\Delta,y)=\phi(x,y)+\frac{\partial \phi}{\partial x}\Delta +\frac{1}{2}\frac{\partial^2 \phi}{\partial x^2}\Delta^2 + \frac{1}{6}\frac{\partial^3 \phi}{\partial x^3}\Delta^3+\frac{1}{24}\frac{\partial^4 \phi}{\partial x^4}\Delta^4 + \mathcal{O}(\Delta^5) \tag{6}$
$\phi(x-\Delta,y)=\phi(x,y)-\frac{\partial \phi}{\partial x}\Delta +\frac{1}{2}\frac{\partial^2 \phi}{\partial x^2}\Delta^2 - \frac{1}{6}\frac{\partial^3 \phi}{\partial x^3}\Delta^3+\frac{1}{24}\frac{\partial^4 \phi}{\partial x^4}\Delta^4 + \mathcal{O}(\Delta^5) \tag{7}$
式(6)と式(7)を足し合わせると,
$\frac{\partial^2 \phi(x,y)}{\partial x^2} = \frac{\phi(x+\Delta,y)+ \phi(x-\Delta,y)-2\phi(x,y)}{\Delta^2} +\mathcal{O}(\Delta^2) \tag{8} $
yに対しても同様にテイラー展開を行って,
$\frac{\partial^2 \phi(x,y)}{\partial y^2} = \frac{\phi(x,y+\Delta)+ \phi(x,y-\Delta)-2\phi(x,y)}{\Delta^2} +\mathcal{O}(\Delta^2) \tag{9} $
を得る。
式(8),(9)を(5)へ代入し少し整理して,
$
\phi(x,y) = \frac{1}{4} [\phi(x+\Delta,y)+\phi(x-\Delta,y)+\phi(x,y+\Delta)+\phi(x,y-\Delta)]+\frac{\rho(x,y)}{4 \epsilon_0}\Delta^2+\mathcal{O}(\Delta^4) \tag{10}
$
を得る。これはポアソン方程式の差分表現である。
誤差は$\mathcal{O}(\Delta^4)$である。
$\rho(x,y)=0$のときに
$\phi(x,y) = \frac{1}{4} [\phi(x+\Delta,y)+\phi(x-\Delta,y)+\phi(x,y+\Delta)+\phi(x,y-\Delta)]+\mathcal{O}(\Delta^4) \tag{11} $
となる。これはラプラス方程式の差分表現である。
数値計算では,配列の添え字を$(x_i,y_j)$とすると式(10)は
$
\phi(x_i,y_j) = \frac{1}{4} [\phi(x_{i+1},y_{j})+\phi(x_{i-1},y_{j})+\phi(x_{i},y_{j+1})+\phi(x_{i},y_{j-1})]+\frac{\rho(x_{i},y_{j})}{4\epsilon_0}\Delta^2 \tag{12}
$
となる。
点$(x_i,y_j)$における電位$\phi(i,j)$は周囲の4点の値の平均値に電荷密度$\rho(x,y)$に比例した量を足すことで近似される(下図)。
**はじめに境界条件と領域内でのポテンシャルの推定値を与え,式(12)を全領域で解き,領域内の解が収束するまで繰り返す。これがヤコビ法である。**収束のための繰り返しステップ数はデータ点数のおよそ二乗に比例する[1]。
この方法は収束が大変遅く実用的ではないが,現代的な方法を理解するための基盤となる。
参考文献
ヤコビ法はおよびそれを若干改した善計算手法であるガウス-ザイデル法では収束が遅く実用的ではない。より速いスキームとして逐次過緩和法(SOR法)などがある[1,2]。
[1] 「ニューメリカルレシピ・イン・シー 日本語版―C言語による数値計算のレシピ」技術評論社,1993.
ネットで閲覧可能なものとしてのとして,
と
を挙げておく。
追記: 2017年8月14日
SOR法,ガウスザイデル法に関する記事を投稿した。
[2] Qiita記事, [Pythonによる科学・技術計算] ラプラス方程式に対するヤコビ法・ガウス-ザイデル法・SOR法の収束速度の比較,偏微分方程式,境界値問題,数値計算
追記: SOR法によるポアソン方程式を解くコード
[2]の記事で説明したSOR法で例題(2)のポアソン方程式を解くコードを掲載する。
ヤコビ方よりも十倍以上はやく収束するので,こちらを使うと良い。
"""
ポアソン方程式: 数値解法, SOR法
電場も表示:
14 Aug. 2017
"""
%matplotlib nbagg
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import ArtistAnimation # アニメーション作成のためのメソッドをインポート
import matplotlib.animation as animation
anim = []
#
delta_Lx=0.01
delta_Ly=0.01
LLx = 1 # 正方形の幅
LLy= 1
Lx = int(LLx/delta_Lx)
Ly = int(LLy/delta_Ly)
V = 5.0 # 電圧
convegence_criterion = 10**-5
phi = np.zeros([Lx+1,Ly+1])
phi_Bound= np.zeros([Lx+1,Ly+1])
phi_Bound[0,:] = V # 境界条件
# 電荷密度の設定
eps0=1
charge= np.zeros([Lx+1,Ly+1])
c=1000
CC=int(Lx/4)
CC2=int(Ly/2)
for i in range(CC, CC2+1):
for j in range(CC,CC2+1):
charge[i,j] = c
#
# for SOR method
aa_recta=0.5*(np.cos(np.pi/Lx)+np.cos(np.pi/Ly))
omega_SOR_recta = 2/(1+np.sqrt(1-aa_recta**2)) # SOR法における加速パラメータ
print("omega_SOR_rect=",omega_SOR_recta)
# for plot
im=plt.imshow(phi,cmap='hsv')
anim.append([im])
# メイン
delta = 1.0
n_iter=0
conv_check=[]
while delta > convegence_criterion:
phi_in=phi.copy()
if n_iter % 100 ==0: # 収束状況のモニタリング
print("iteration No =", n_iter, "delta=",delta)
conv_check.append([n_iter, delta])
for i in range(Lx+1):
for j in range(Ly+1):
if i ==0 or i ==Lx or j==0 or j==Ly:
phi[i,j] = phi_Bound[i,j]
else:
phi[i,j] = phi[i,j]+omega_SOR_recta *((phi[i+1,j] + phi[i-1,j] + phi[i,j+1] + phi[i,j-1])/4-phi[i,j]+ (delta_Lx*delta_Ly/(4*eps0))*charge[i,j]) # SOR = ガウス-ザイデル + OR
delta = np.max(abs(phi-phi_in))
n_iter+=1
im=plt.imshow(phi,cmap='hsv')
anim.append([im])
# for plot
pp=plt.colorbar (orientation="vertical") # カラーバーの表示
pp.set_label("phi", fontname="Ariel", fontsize=24)
plt.xlabel('X',fontname="Ariel", fontsize=24)
plt.ylabel('Y',fontname="Ariel", fontsize=24)
plt.title('Solution of the Poisson equation for electrostatic potential ')
# ani = ArtistAnimation(fig, anim, interval=10, blit=True,repeat_delay=1000)
# ani.save("t.gif", writer='imagemagick')
plt.show()
# 電場の計算
Ex = np.zeros([Lx,Ly])
Ey = np.zeros([Lx,Ly])
for i in range(Lx):
for j in range(Ly):
Ex[i,j] = -(phi[i+1,j]-phi[i,j])/delta_Lx
Ey[i,j] = -(phi[i,j+1]-phi[i,j])/delta_Ly
plt.figure()
X, Y= np.meshgrid(np.arange(0, Lx,1), np.arange(0, Ly,1)) # メッシュ生成
plt.quiver(X,Y,Ex,Ey,color='red',angles='xy',scale_units='xy', scale=40) # ベクトル場をプロット
plt.xlim([0,Lx]) # 描くXの範囲
plt.ylim([0,Ly]) # 描くyの範囲
# グラフ描画
plt.grid()
plt.draw()
plt.show()