はじめに
$y(x)$に対する常微分方程式が同次線形であり,かつ以下のようにパラメータ(固有値)$\lambda$についても線形である場合は,境界値問題を行列の固有値問に帰着させ,その行列方程式を解くことで常微分方程式の解(固有関数)および固有値を決定することが可能である[1]。
初期値問題として常微分方程式を積分して解く方法(射撃法[2]など)よりも実装が簡単である。
ここでは2階常微分方程式を考えよう。
$p(x)y''(x)+q(x)y'(x)+r(x)y(x) = \lambda (u(x)y''(x)+v(x)y'(x)+w(x)y(x)) {\tag 1}$
同時境界条件として,
$y(x_0)=0, y(x_N)=0 {\tag2}$
を考える。
区間 $x= [x_0,x_1]$をN等分し
$\delta x = (x_1-x_0)/N{\tag 3}$
$x_i=x_0+i\ \delta x{\tag 4}$
$y_i=y(x_i) {\tag 5}$
とする。
さて,導関数$y''(x)$および$y'(x)$を中心差分近似で評価すると
$y'(x) = \frac{y_{i+1}-y_{i-1}}{2 \delta x} +O(\delta x^3){\tag 6}$
$y''(x) = \frac{y_{i+1}-2y_{i}+y_{i-1}}{\delta x ^2}+O(\delta x^3) {\tag 7}$
と表現できる。
これらの近似によって(1)を解いたときの固有値・固有関数には$O(\delta x^2)$の誤差が含まれる。
式(5,6)を式(1) に代入し整理すると,問題を行列形式による一般固有値問題として表現できる。
$ A \ \mathbf{y} = \lambda \ B \ \mathbf{y} \ {\tag 8}$
ここで$\mathbf{y}$は解ベクトルである。
$\mathbf{y}=(y_1, y_2, y_3, ...., y_{N-1}) {\tag 9}$
$A=(a_{ij})$および$B=(b_{ij})$は$N-1$次元の行列であり,3重対角行列である。
それらの行列要素は$i=1,2,...,N-1$として,
$a_{i,i-1}=\frac{p_i}{\delta x^2}+\frac{q_i}{2 \delta x}, \ a_{i,i}=\frac{-2p_i}{\delta x^2}+r_i, \ a_{i,i+1}= \frac{p_i}{\delta x^2}-\frac{q_i}{2 \delta x} {\tag {10}}$
$a_{i,j} = 0 \ ( j\neq i-1, i, i+1){\tag {11}}$
$b_{i,i-1}=\frac{u_i}{\delta x^2}+\frac{v_i}{2 \delta x}, \ b_{i,i}=\frac{-2u_i}{\delta x^2}+w_i, \ b_{i,i+1}= \frac{u_i}{\delta x^2}-\frac{v_i}{2 \delta x} {\tag {12}}$
$b_{i,j} = 0 \ ( j\neq i-1, i, i+1){\tag {13}}$
と表される。
式(8)はPythonのライブラリ(numpy・scipyなど)を利用して解くことができる[3]。
本稿ではこの方法を用いて簡単な例題を解いてみる。
#なお,この方法は,解を適当な関数系で展開しその係数に対する行列方程式を求める関数展開法(スペクトル法)とは異なる。
内容
2階同次常微分方程式の境界値問題 (単振動)
$y''(x)=-\lambda y, \ (y(0)=y(1)=0)$
を行列による方法で解く。
この場合,式(1)の各関数は,
$p(x)=1, q(x)=0, r(x)=0, u(x)=0, v(x)=0, w(x)=1 {\tag {14}}$
となり,
$ A \ \mathbf{y} = \lambda \ B \ \mathbf{y} $において,$A$は,
$a_{i,i-1}=\frac{1}{\delta x^2}, \ a_{i,i}=\frac{-2}{\delta x^2}, \ a_{i,i+1}= \frac{1}{\delta x^2} {\tag {15}}$
であり,
$B$は,単位行列$E$によって
$B = -E{\tag {16}}$
と表される。
あとはこれらの行列に対して
$ A \ \mathbf{y_n} = - \lambda_n \ E \ \mathbf{y} {}\tag {17} $
を解き,固有値$\lambda_n$とそれに対応する固有関数$y_n(x)$を求める。
コード
scipy.linalg.eigを用いて一般固有値問題(式17)を解く[3]。
"""
行列法による境界値問題の解法
"""
import numpy as np
import scipy.linalg
import matplotlib.pyplot as plt
delta_x = 0.025
x0, x1 = 0, 1 #境界のx座標
N=int((x1-x0)/delta_x) # データグリッド数
print("N=",N)
y = np.zeros([N-1,N+1])
# 同時境界条件
y[:,0] = 0
y[:,-1] = 0
A=np.zeros([N-1,N-1])
B=-np.identity(N-1) # B= -E
# 行列Aの構築
for i in range(N-1): # 3重対角行列なのでindexの位置を気をつけること
if i == 0:
A[i,i] = -2/(delta_x**2)
A[i,i+1] = 1/(delta_x**2)
elif i == N-2:
A[i,i-1] = 1/(delta_x**2)
A[i,i] = -2/(delta_x**2)
else:
A[i,i-1] = 1/(delta_x**2)
A[i,i] = -2/(delta_x**2)
A[i,i+1] = 1/(delta_x**2)
#
eigen, vec= scipy.linalg.eig(A,B) # 一般固有値問題を解き,固有値を"eigen",固有関数を"vec"というオブジェクトへ格納する
print("eigen values=",eigen)
# print("eigen vectors=",vec)
for j in range(N-1):
for i in range(1,N):
y[j, i] = vec[i-1,j]
#
# for plot
X= np.linspace(x0,x1, N+1)
plt.plot(X, y[0,:],'-',markersize=5,label='y1')
plt.plot(X, y[1,:],'-',markersize=5,label='y2')
plt.plot(X, y[2,:],'-',markersize=5,label='y3')
plt.legend(loc='upper right')
plt.xlabel('X') # x軸のラベル
plt.ylabel('Y') # y軸のラベル
plt.show()
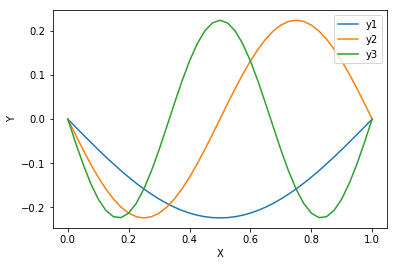
結果
固有値を小さい順に最初の3つを表示する。左から$\lambda_1$, $\lambda_2$,$\lambda_3$である。
eigen values= [ 9.86453205+0.j 39.39731010+0.j 88.41625473+0.j]
これらの固有値に対応する固有関数$y_1(x)$,$y_2(x)$,$y_3(x)$を図に示す。
参考文献
[1]名取亮,『数値解析とその応用 コンピュータ数学シリーズ15』,コロナ社, 1990.
[2]射撃法を用いた常微分方程式の解法例: [Pythonによる科学・技術計算] 定常状態の一次元シュレディンガー方程式の射撃法による解法(2),調和振動子ポテンシャル,量子力学
[3] 行列の固有値・固有ベクトル(関数)をライブラリを使って求める方法: [Pythonによる科学・技術計算] numpy・scipyを用いた(一般化)固有値問題の解法,ライブラリ利用