はじめに
Qiuita記事,
[Pythonによる科学・技術計算] 定常状態の一次元シュレディンガー方程式の射撃法による解法(1),井戸型ポテンシャル,量子力学
では井戸型ポテンシャルに対する固有値問題を射撃法[1] + ヌメロフ法[2]で解いた。本稿では調和振動子ポテンシャルに対する固有値問題を同様の手法を用いて解く。
上のQiita記事でも述べたが,射撃法を用いたPythonコードはネットでなかなか見つからないのが現状である(2017年9月4日現在)。本記事が読者の量子力学の理解を深めることに少しでも貢献できれば幸いである。
問題設定
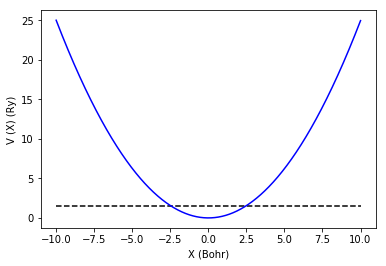
調和振動子ポテンシャル $V(x)$は
$V(x) = \frac{m\omega^2x^2}{2} {\tag1}$
で与えられる。
図. 調和振動子ポテンシャル。点線はE=1.5Ryとしたもの。
これに対応する定常状態のシュレディンガー方程式は,
$\frac{d^2}{d x^2}\psi(x) +k^2(x) \psi =0 {\tag 2}$
$k^2(x) = \frac{2m}{\hbar^2}(E-\frac{m\omega^2x^2}{2}) {\tag 3}$
である。
Rydberg原子単位と呼ばれる単位系,
電子の質量$m=1/2$
ディラック定数$\hbar =1$
長さをボーア$a_{B}=(0.529177 Å)$単位,
エネルギーを$1Ry=13.6058 eV = $
を用いると,シュレディンガー方程式は
$\frac{d^2}{d x^2}\psi(x) +k^2(x) \psi =0 $
$k^2(x) = (E-\frac{\omega^2x^2}{4}) {\tag 4}$
となる。
調和振動子ポテンシャルに対する第$n(n=0,1,2,...)$番固有値$E_n$の厳密解は,
$E_n = (n+\frac{1}{2})(\hbar \omega), (n=0,1,2,...){\tag 5}$
である。本コードでは$\hbar=1$, $\omega=1$としているので,
$E_0 = 0.5$
$E_1 = 1.5$
$E_2= 2.5$
$E_3= 3.5$
...
である。
規格化された固有関数$\psi_n$の厳密解は以下のようになる。
$\psi_n(x)=AH_n(\xi)\exp\left(-\frac{\xi^2}{2}\right) {\tag 6}$
ここで$\xi$と$A$は以下で与えられる。
$\xi=\sqrt{\frac{m\omega}{\hbar}}x,\ A=\sqrt{\frac{1}{n!2^n}\sqrt\frac{m\omega}{\pi\hbar}}, {\tag 7}$
また,$H_n$はエルミート多項式である。
$H_n(x)=(-1)^n\exp\left(x^2\right)\frac{\mathrm{d}^n}{\mathrm{d}x^n}\exp\left(-x^2\right) {\tag 8}$
これらを数値計算によって求めることが本稿の目的である。
解の評価法
本記事に掲載したコードでは問題の解の評価法を以下のように設定している。
波動関数は連続関数であり,かつ,その一次微分も連続である。
波動関数の持つこの性質を満たす1つの必要条件として波動関数の対数の微分
$\frac{d (\ln\ \psi(x))}{dx} = \frac{\psi'(x)}{\psi(x)} {\tag 9}$
が連続という条件を課すことができる。さらに波動関数の規格化を行えば,最終的に正しい解を得られる。
そこで,
左側と右側から積分した解(それぞれ$\psi_L(x)$と$\psi_R(x)$とする)をチェックする点$x=x_m$において,解の評価関数として
$\Delta E(\epsilon, x=x_m) =\frac{\psi_L'(x_m)}{\psi_L(x_m)}-\frac{\psi_R'(x_m)}{\psi_R(x_m)} {\tag {10}}$
を考える。
$\Delta E(\epsilon, x=x_m) =0$となるとき,$\epsilon$は正しいエネルギー固有値となる。$\Delta E(\epsilon, x=x_m)$を$\epsilon$の関数としてあるエネルギー範囲Emin からEmaxまで次々に計算していき,$\Delta E$が一定値より小さくなったときを解とみなすことができる。
ところで式(10)は非常に大きな値をとることがあり,数値評価がしにくくなる場合がある。そこで$\Delta E(\epsilon)$のスケールを調整するため,そこで本記事に掲載したコードでは式(10)の分母にスケール調整因子(対数微分の和)をかけたものを$\Delta E$として採用している。もちろん,このようにしても得られる解に変わりはない。
$\Delta E(\epsilon, x=x_m) =(\frac{\psi_L'(x_m)}{\psi_L(x_m)}-\frac{\psi_R'(x_m)}{\psi_R(x_m)})/(\frac{\psi_L'(x_m)}{\psi_L(x_m)}+\frac{\psi_R'(x_m)}{\psi_R(x_m)}) {\tag {11}}$
コード
(1)両端からの解の整合生をチェックするxの値の選び方や,(2)解の対称性と初期条件の選び方について,幾つかの注意点を補遺で述べたのでコードの詳細を知りたい方は一読されたい。**
"""
射撃法+ヌメロフ法による時間に依存しない一次元シュレディンガー方程式の解法
調和振動子ポテンシャル
3 Sept. 2017
"""
import numpy as np
import matplotlib.pyplot as plt
iter_max = 100
delta_x=0.01
xL0, xR0 = -10, 10
E=1.5
eps_E=0.01
# nn=4
hbar=1
omega=1
m_elec=0.5
def calc_match_pos_osci(E):
xa =np.sqrt(2*E/(m_elec*(omega**2)))# 転回点
return xa
xa = calc_match_pos_osci(E) # 転回点
print("xa=",xa)
# xL0, xR0 = -nn*xa, nn*xa
Nx = int((xR0-xL0)/delta_x)
i_match = int((xa-xL0)/delta_x) #uLとuRの一致具合をチェックする位置のインデックス。転回点に選ぶ。
nL = i_match
nR = Nx-nL
print(xL0,xR0, i_match, delta_x)
print(nL,nR)
uL = np.zeros([nL],float)
uR = np.zeros([nR],float)
print("E= ",E)
print("xL0,xR0, i_match, delta_x=",xL0,xR0, i_match, delta_x)
print("Nx, nL,nR=",Nx, nL,nR)
def V(x): #調和振動子ポテンシャル
v = m_elec*(omega**2)*(x**2)/2
return v
# 境界条件・初期条件セット
def set_condition_even(): # 偶関数
uL[0] = 0
uR[0] = 0
uL[1] = 1e-12
uR[1] = 1e-12
def set_condition_odd(): # 奇関数
uL[0] = 0
uR[0] = 0
uL[1] = -1e-12
uR[1] = 1e-12
set_condition_even()
def setk2 (E): # for E<0
for i in range(Nx+1):
xxL = xL0 + i*delta_x
xxR = xR0 - i*delta_x
k2L[i] = (2*m_elec/hbar**2)*(E-V(xxL))
k2R[i] =(2*m_elec/hbar**2)*(E-V(xxR))
def Numerov (N,delta_x,k2,u): # ヌメロフ法による計算
b = (delta_x**2)/12.0
for i in range(1,N-1):
u[i+1] = (2*u[i]*(1-5*b*k2[i])-(1+b*k2[i-1])*u[i-1])/(1+b*k2[i+1])
xL=np.zeros([Nx])
xR=np.zeros([Nx])
for i in range (Nx):
xL[i] = xL0 + i*delta_x
xR[i] = xR0 - i*delta_x
k2L=np.zeros([Nx+1])
k2R=np.zeros([Nx+1])
setk2(E)
def E_eval(): # 評価関数: 式(11)を参照
# print("in E_eval")
# print("delta_x=",delta_x)
if uL[-1]*uR[-1] >0 : # 符号が違うと偶然logderiが一致してしまうときがあるので,同符号という条件をつける (固有値をみつけるだけなら関係ない)
uLdash = (uL[-1]-uL[-2])/delta_x
uRdash = (uR[-2]-uR[-1])/delta_x
logderi_L= uLdash/uL[-1]
logderi_R= uRdash/uR[-1]
# print("logderi_L, R=",logderi_L,logderi_R)
return (logderi_L- logderi_R)/(logderi_L+logderi_R) #式(9)
else:
return False
# ポテンシャル関数のプロット
XXX= np.linspace(xL0,xR0, Nx)
POT=np.zeros([Nx])
for i in range(Nx):
POT[i] = V(xL0 + i*delta_x)
plt.xlabel('X (Bohr)') # x軸のラベル
plt.ylabel('V (X) (Ry)') # y軸のラベル
plt.hlines([E], xL0,xR0, linestyles="dashed") #Energy
plt.plot(XXX,POT,'-',color='blue')
plt.show()
#
# k^2(x)のplot
plt.xlabel('X (Bohr)') # x軸のラベル
plt.ylabel('k^2 (X) (Ry)') # y軸のラベル
XXX= np.linspace(xL0,xR0, len(k2L[:-2]))
plt.plot(XXX, k2L[:-2],'-')
plt.show()
#
def normarize_func(u):
factor = ((xR0-xL0)/Nx)*(np.sum(u[1:-2]**2))
return factor
def plot_eigenfunc(color_name):
uuu=np.concatenate([uL[0:nL-2],uR[::-1]],axis=0)
XX=np.linspace(xL0,xR0, len(uuu))
factor=np.sqrt(normarize_func(uuu))
# print("fcator = ",factor)
plt.plot(XX,uuu/factor,'-',color=color_name,label='Psi')
plt.plot(XX,(uuu/factor)**2,'-',color='red',label='| Psi |^2')
plt.xlabel('X (Bohr)') # x軸のラベル
plt.ylabel('') # y軸のラベル
plt.legend(loc='upper right')
plt.show()
# 解の探索
# 境界条件1 (偶関数)
EEmin=0.1
EEmax = 5
delta_EE=0.01
NE = int((EEmax-EEmin)/delta_EE)
Elis=[]
Solved_Eigenvalu=[]
check_Elis= []
for i in range(NE+1):
EE=EEmin+i*(EEmax-EEmin)/NE
xa = calc_match_pos_osci(EE) # 転回点
i_match = int((xa-xL0)/delta_x) #uLとuRの一致具合をチェックする位置のインデックス。転回点にえらぶ。
nL = i_match
nR = Nx-nL
uL = np.zeros([nL],float)
uR = np.zeros([nR],float)
set_condition_even()
setk2(EE)
Numerov (nL,delta_x,k2L,uL)
Numerov (nR,delta_x,k2R,uR)
a1= E_eval()
#print ("a1=",a1)
if a1 : # a1がTrueのとき
Elis.append(EE)
check_Elis.append(a1)
if np.abs(a1) <= eps_E :
print("Eigen_value = ", EE)
Solved_Eigenvalu.append(EE)
plot_eigenfunc("blue")
plt.plot(Elis, check_Elis, 'o',markersize=3, color='blue',linewidth=1)
plt.grid(True) #グラフの枠を作成
plt.xlim(EEmin, EEmax) # 描くxの範囲を[xmin,xmax]にする
plt.ylim(-10, 10) # 描くyの範囲を[ymin,ymax]にする
plt.hlines([0], EEmin,EEmax, linestyles="dashed") # y=y1とy2に破線を描く
plt.xlabel('Energy (Ry)') # x軸のラベル
plt.ylabel('Delta_E_function') # y軸のラベル
plt.show()
# 境界条件2 (奇関数)
EEmin=0.1
EEmax = 5
delta_EE=0.01
NE = int((EEmax-EEmin)/delta_EE)
Elis=[]
Solved_Eigenvalu=[]
check_Elis= []
for i in range(NE+1):
EE=EEmin+i*(EEmax-EEmin)/NE
xa = calc_match_pos_osci(EE) # 転回点
i_match = int((xa-xL0)/delta_x) #uLとuRの一致具合をチェックする位置のインデックス。転回点に選ぶ。
nL = i_match
nR = Nx-nL
uL = np.zeros([nL],float)
uR = np.zeros([nR],float)
set_condition_odd()
setk2(EE)
Numerov (nL,delta_x,k2L,uL)
Numerov (nR,delta_x,k2R,uR)
a1= E_eval()
#print ("a1=",a1)
if a1 : # a1がTrueのとき
Elis.append(EE)
check_Elis.append(a1)
if np.abs(a1) <= eps_E :
print("Eigen_value = ", EE)
Solved_Eigenvalu.append(EE)
plot_eigenfunc("blue")
plt.plot(Elis, check_Elis, 'o',markersize=3, color='red',linewidth=1)
plt.grid(True) #グラフの枠を作成
plt.xlim(EEmin, EEmax) # 描くxの範囲を[xmin,xmax]にする
plt.ylim(-10, 10) # 描くyの範囲を[ymin,ymax]にする
plt.hlines([0], EEmin,EEmax, linestyles="dashed") # y=y1とy2に破線を描く
plt.xlabel('Energy (Ry)') # x軸のラベル
plt.ylabel('Delta_E_function') # y軸のラベル
plt.show()
結果
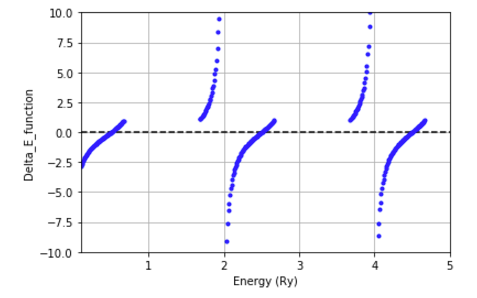
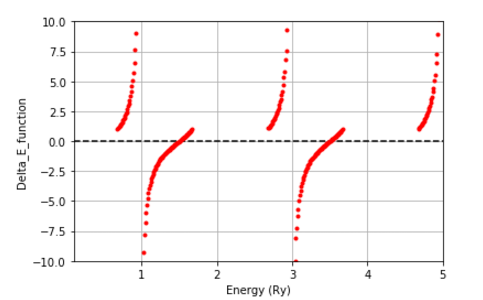
(1) 評価関数
評価関数(式(9)をプロットしたものを示す。ゼロ点がエネルギー固有値の解である。
偶感数解の場合と奇関数解の2種類ある。
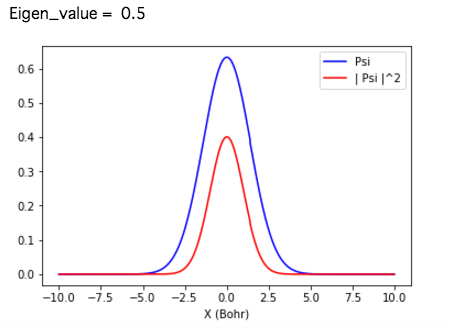
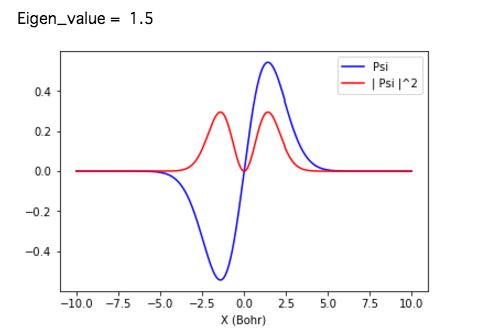
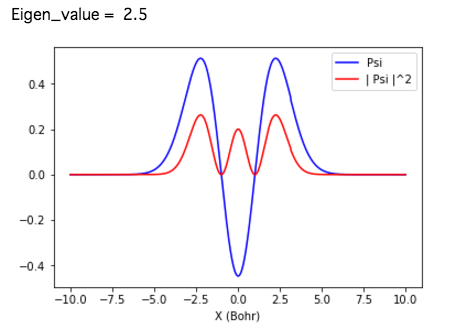
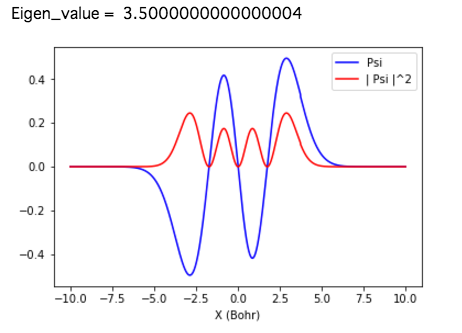
(2) エネルギー固有値と波動関数
得られた固有値と固有関数をいくつか示す。厳密解と極めて良く一致する。
厳密解は,
$E_n = (n+\frac{1}{2})(\hbar \omega), (n=0,1,2,...)$
である。本コードでは$\hbar=1$, $\omega=1$としているので,
$E_0 = 0.5$
$E_1 = 1.5$
$E_2= 2.5$
$E_3= 3.5$
...
である。
補遺
(1) 両端から積分した解をチェックする点をどこに選ぶか
両端から積分した解の整合性のチェックを行う点$x_m$は,古典力学的な運動が禁止される境界(**"転回点"**という)に選んだ。つまり,与えたEの推定値に対して
$E = m \omega^2 x^2 /2 {\tag {12}}$
を満たす$x$を$x_m$とした。すなわち,
$x_m= (\frac{2E}{m\omega^2})^\frac{1}{2} {\tag {13}}$
である
$x_m$を越えて積分すると,微分方程式の解の中に,遠方で発散する解(特殊解)が混じり,数値的に不安定になるためである。
(2) 解の対称性と初期条件
境界条件は
$\lim_{x \to \infty} \psi(x) = 0 {\tag {14}}$
であたえらえる一方,境界における$\frac{d\psi}{dx}$の値は未定である。
両端で一次微分値を与える必要があるが,その符号のとりかたによって得られる解の種類(対称性)が決まる。
そこで本コードではその両方の可能性を考慮するため2つの境界条件を設定し,偶関数解と奇関数解をそれぞれ調べている
参考文献
[1] Qiuita記事,
[Pythonによる科学・技術計算] 定常状態の一次元シュレディンガー方程式の射撃法による解法(1),井戸型ポテンシャル,量子力学
[2] Qiita記事 [Pythonによる科学・技術計算]ヌメロフ法による2階常微分方程式の解法,数値計算
[3] 阿部正典 ほか(訳),『クーニン 計算機物理学』
調和振動子ポテンシャルに対するシュレディンガー方程式についてはどの量子力学のテキストにも載っているが,初学者に配慮しわかりやすく書かかれている以下の本を挙げておく。
[4] 鈴木 克彦, 『シュレディンガー方程式 ―基礎からの量子力学攻略』